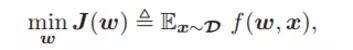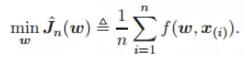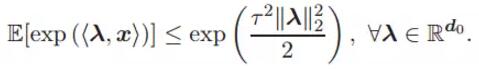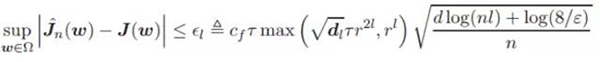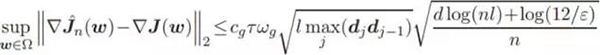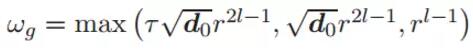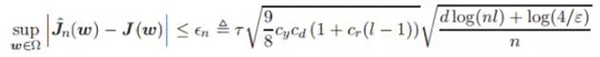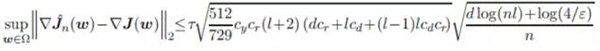論文地址：https://arxiv.org/abs/1705.07038

本論文通過理論分析深度神經網絡群體風險(population risk)的收斂行為和它的駐點(stationary point)與屬性來研究深度學習的經驗風險(empirical risk)全景圖。對于 L 層的線性神經網絡，我們證明其經驗風險一致收斂到訓練樣本大小為 n、比率(rate)為的群體風險，其中 d 是總權重維度、r 是每一層權重的量級范圍。然后，我們基于這一結果推導出經驗風險的穩定性和泛化邊界。此外，我們確立了經驗風險梯度與群體風險梯度的收斂一致性。我們同樣證明了經驗風險和群體風險之間的非退化(non-degenerate)駐點和收斂的對應關系，這就描述了深度神經網絡算法的全景圖。此外，我們同樣分析了用 Sigmoid 函數作為激活函數的深度非線性神經網絡的特性。我們證明了深度非線性神經網絡經驗風險梯度的收斂行為和線性一樣，并同時分析了其非退化駐點的性質。

據我們所知，該研究是***次理論上描述深度學習算法全景圖(landscape)的工作。此外，我們的研究結果為訓練良好的深度學習算法提供了樣本復雜度(sample complexity)。我們同樣提供了神經網絡深度 L、層級寬度、網絡規模 d 和參數量級如何決定神經網絡格局的理論理解。

1. 簡介

深度學習算法已經在很多領域取得了令人矚目的成果，比如計算機視覺 [1, 2, 3]、自然語言處理 [4, 5] 和語音識別 [6, 7] 等等。然而，由于其高度非凸性和內在復雜性，我們對這些深度學習算法屬性的理論理解依然落后于其實際成就。事實上，深度學習算法經常通過最小化經驗性風險來學習其模型參數。因此我們致力于分析深度學習算法的經驗風險全景圖以更好地理解其實際表現。

正式地，我們考慮由 L 層網絡 (L ≥ 2) 組成的深度神經網絡模型，并通過最小化常用的平方損失函數(來自未知分布 D 的樣本)進行訓練。理想情況是深度學習算法可通過最小化群體風險找到其***參數 w∗。

其中 w 是模型參數，

該方程為樣本 x 服從分布 D 的平方損失函數。這里 v (l) 是第 l 層的輸出，y 是樣本 x 的目標輸出。實際上，由于樣本分布 D 經常未知，并且只有有限的訓練樣本 x(i)，以及來自 D 的，所以常常通過最小化經驗風險以訓練網絡模型。

在這項工作中，通過將經驗風險收斂到群體風險 J(w) 及其駐點和屬性的分析，我們同時為多層線性和非線性神經網絡描述了深度學習算法經驗風險的全景圖。

2. 文獻綜述

到目前為止，只有少數理論可以解釋深度學習，并且它們可大致被分為三類。

• ***類旨在分析深度學習的訓練誤差。
• 第二類的工作 [13, 14, 9, 15] 致力于分析深度學習之中高度非凸性損失函數的損失曲面，如駐點的分布。
• 第三類是一些最近的工作，其試圖把問題分解為更小的部分來試圖降低分析難度。

然而，還沒有分析深度學習算法經驗風險全部格局的工作。

3. 深度線性神經網絡的研究結果

我們首先證明了深度線性神經網絡經驗風險到群體風險的一致收斂性(uniform convergence)。基于該項證明，我們推導出了穩定性和泛化邊界(generalization bounds)。隨后，我們提出了經驗梯度(empirical gradient)和群體梯度之間的一致性收斂保證，然后還分析了經驗風險非退化駐點的性質。

在本論文的分析中，我們假定輸入數據 x 服從τ^2 -sub-Gaussian 分布，同時如假設 1(Assumption 1)所述存在受限量級。

假設 1. 輸入數據，其均值為 0 且服從 τ^2 -sub-Gaussian 分布。因此 x 就滿足

此外，x 的 L2 范數滿足(x 的量級受限)：

其中 rx 為正項通用常數。

3.1 一致性收斂、經驗風險的穩定性和泛化性

定理 1 確定了深度線性神經網絡經驗風險的一致收斂性結果。

定理 1： 假定假設 1 中的輸入數據 x 在深度神經網絡中的激活函數是線性的。那么存在兩個通用常數 cf ′ 和 cf，且滿足：

那么，就存在：

該不等式的置信度至少為 1 − ε。其中 l 為神經網絡層級數量、n 為樣本規模、dl 為***一層的維度大小。

3.2 梯度的一致性收斂

在這一部分中，我們分析了深度線性神經網絡的經驗風險和群體風險的梯度收斂性。梯度收斂的結果對描繪神經網絡算法的全景圖十分有效。我們的結果展現在下面。

定理 2 ：假定假設 1 中的輸入數據 x 在深度神經網絡中的激活函數是線性的。經驗風險梯度在 L2 范數(歐幾里德范數)中收斂到群體風險梯度。特別地，若

其中 cg' 為通用常數，那么存在通用常數 cg 滿足：

該不等式的置信度至少為 1 − ε，其中

3.3 駐點的一致性收斂

這里我們分析了在優化深度學習算法經驗風險時的駐點屬性。為了簡化起見，我們使用了幾何性孤立(geometrically isolated)的非退化駐點，因此該駐點局部中是唯一的。

4. 深度非線性神經網絡的結果

在以上章節，我們分析了深度線性神經網絡模型的經驗風險優化全景圖。在本節中，我們接著分析深度非線形神經網絡，它采用了 sigmoid 激活函數并在實踐之中更受歡迎。值得注意的是，我們的分析技巧也適用于其他三階微分函數，比如 帶有不同收斂率的 tanh 函數。這里我們假設輸入數據是高斯變量(i.i.d. Gaussian variables)。

4.1 一致性收斂、經驗風險的穩定性和泛化

本章節中，我們首先給出經驗風險的一致收斂分析，接著分析其穩定性(Stability)和泛化。

定理 4. 假定輸入樣本 x 服從假設 2，并且深度神經網絡的激活函數是 sigmoid 函數，那么如果

那么存在通用的常數 cy，滿足：

該不等式的置信度至少為 1−ε，其中

4.2 梯度和駐點的一致性收斂

在這一部分中，我們分析了深度非線性神經網絡經驗風險的梯度收斂性質。

定理 5 假定輸入樣本 x 服從假設 2，并且深度神經網絡中的激活函數為 sigmoid 函數。那么經驗風險的梯度以 L2 范數(歐幾里德范數)的方式一致收斂到群體風險的梯度。特別地，如果

其中 cy' 為常數，那么有：

該不等式的置信度至少為 1 − ε，其中 cy、 cd 和 cr 是在定理 4 中的相同參數。

6. 證明概覽

在該章節中，我們將簡單介紹證明的過程，不過由于空間限制，定理 1 到 6、推論 1 到 2、還有技術引理在補充材料中展示。

7. 結論

在這項工作中，我們提供了深度線性/非線性神經網絡經驗風險優化全景圖的理論分析，包括一致性收斂、穩定性和經驗風險本身的泛化及其梯度和駐點的屬性。我們證明了經驗風險到群體風險的收斂率為。這些結果同樣揭示了神經網絡深度(層級數)l、網絡大小及寬度對收斂率至關重要。我們也證明了權重參數的量級在收斂速度上也扮演著重要角色。事實上，我們建議使用小量級權重數。所有的結果與實踐中廣泛使用的網絡架構相匹配。

【本文是51CTO專欄機構“機器之心”的原創譯文，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文