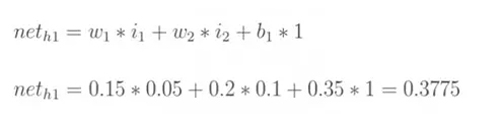以撩妹為例,5分鐘讓你秒懂深度學習!
原創【51CTO.com原創稿件】今天,面對 AI 如此重要的江湖地位,深度學習作為重要的一個研究分支,幾乎出現在當下所有熱門的 AI 應用領域,其中包含語義理解、圖像識別、語音識別,自然語言處理等等,更有人認為當前的人工智能等同于深度學習領域。
如果在這個人工智能的時代,作為一個有理想抱負的程序員,或者學生、愛好者,不懂深度學習這個超熱的話題,似乎已經跟時代脫節了。
但是,深度學習對數學的要求,包括微積分、線性代數和概率論與數理統計等,讓大部分的有理想抱負青年踟躕前行。那么問題來了,理解深度學習,到底需不需要這些知識?
關于深度學習,網上的資料很多,不過大部分都不太適合初學者。楊老師總結了幾個原因:
深度學習確實需要一定的數學基礎。如果不用深入淺出地方法講,有些讀者就會有畏難的情緒,因而容易過早地放棄。
中國人或美國人寫的書籍或文章,普遍比較難。
深度學習所需要的數學基礎并沒有想象中的那么難,只需要知道導數和相關的函數概念即可。假如你高等數學也沒學過,很好,這篇文章其實是想讓文科生也能看懂,只需要學過初中數學。
不必有畏難的情緒,我比較推崇李書福的精神,在一次電視采訪中,李書福說:誰說中國人不能造汽車?造汽車有啥難的,不就是四個輪子加兩排沙發嘛。當然,他這個結論有失偏頗,不過精神可嘉。
“王小二賣豬”解讀深度學習之導數
導數是什么?
無非就是變化率,比如:王小二今年賣了 100 頭豬,去年賣了 90 頭,前年賣了 80 頭。。。變化率或者增長率是什么?每年增長 10 頭豬,多簡單。
這里需要注意有個時間變量---年。王小二賣豬的增長率是 10頭/年,也就是說,導數是 10。
函數 y = f(x) = 10x + 30,這里我們假設王小二第一年賣了 30 頭,以后每年增長 10 頭,x代表時間(年),y代表豬的頭數。
當然,這是增長率固定的情形,而現實生活中,很多時候,變化量也不是固定的,也就是說增長率不是恒定的。
比如,函數可能是這樣: y = f(x) = 5x² + 30,這里 x 和 y 依然代表的是時間和頭數,不過增長率變了,怎么算這個增長率,我們回頭再講。或者你干脆記住幾個求導的公式也可以。
深度學習還有一個重要的數學概念:偏導數
偏導數的偏怎么理解?偏頭疼的偏,還是我不讓你導,你偏要導?
都不是,我們還以王小二賣豬為例,剛才我們講到,x 變量是時間(年),可是賣出去的豬,不光跟時間有關啊,隨著業務的增長,王小二不僅擴大了養豬場,還雇了很多員工一起養豬。
所以方程式又變了:y = f(x) = 5x₁² + 8x₂ + 35x₃ + 30
這里 x₂ 代表面積,x₃ 代表員工數,當然 x₁ 還是時間。
以撩妹為例,解讀深度學習之“偏導數”
偏導數是什么
偏導數無非就是多個變量的時候,針對某個變量的變化率。在上面的公式里,如果針對 x₃ 求偏導數,也就是說,員工對于豬的增長率貢獻有多大。
或者說,隨著(每個)員工的增長,豬增加了多少,這里等于 35---每增加一個員工,就多賣出去 35 頭豬。
計算偏導數的時候,其他變量都可以看成常量,這點很重要,常量的變化率為 0,所以導數為 0,所以就剩對 35x₃ 求導數,等于 35。對于 x₂ 求偏導,也是類似的。
求偏導,我們用一個符號表示:比如 y / x₃ 就表示 y 對 x₃ 求偏導。
廢話半天,這些跟深度學習到底有啥關系?當然有關系,深度學習是采用神經網絡,用于解決線性不可分的問題。
這里我主要講講數學與深度學習的關系。先給大家看幾張圖:
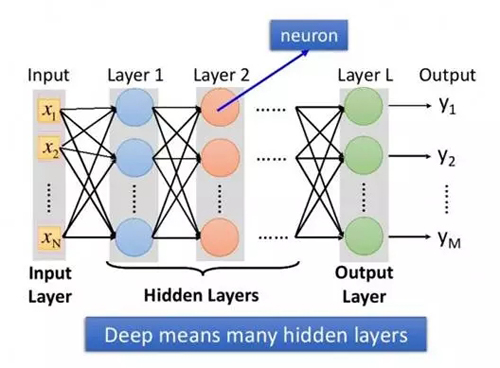
圖1:所謂深度學習,就是具有很多個隱層的神經網絡
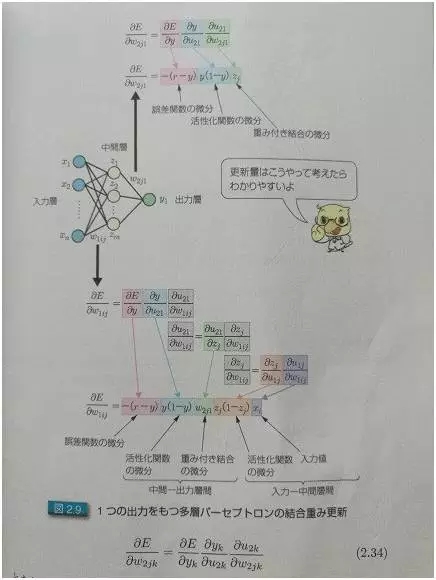
圖2:單輸出的時候,怎么求偏導數
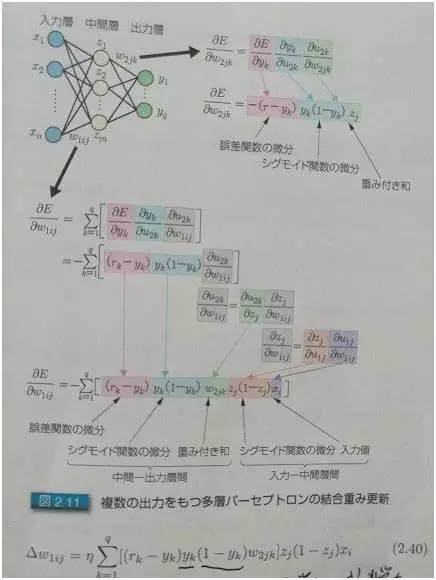
圖3:多輸出的時候,怎么求偏導數
后面兩張圖是日本人寫的關于深度學習的書里面的兩張圖片。所謂入力層,出力層,中間層,分別對應于中文的:輸入層,輸出層,和隱層。
大家不要被這幾張圖嚇著,其實很簡單,就以撩妹為例。男女戀愛我們大致可以分為三個階段:
- 初戀期。相當于深度學習的輸入層。別人吸引你,肯定是有很多因素,比如:身高,身材,臉蛋,學歷,性格等等,這些都是輸入層的參數,對每個人來說權重可能都不一樣。
- 熱戀期。我們就讓它對應隱層吧!這個期間,雙方各種磨合,柴米油鹽醬醋茶。
- 穩定期。對應輸出層,是否合適,就看磨合得咋樣了。大家都知道,磨合很重要,怎么磨合呢?就是不斷學習訓練和修正的過程!
比如女朋友喜歡草莓蛋糕,你買了藍莓的,她的反饋是 negative,你下次就別買了藍莓,改草莓了。
看完這個,有些小伙可能要開始對自己女友調參了。有點不放心,所以補充一下。撩妹和深度學習一樣,既要防止欠擬合,也要防止過擬合。
所謂欠擬合,對深度學習而言,就是訓練得不夠,數據不足,就好比,你撩妹經驗不足。要做到擬合,送花當然是最基本的,還需要提高其他方面,比如,提高自身說話的幽默感等。這里需要提一點,欠擬合固然不好,但過擬合就更不合適了。
過擬合跟欠擬合相反,一方面,如果過擬合,她會覺得你有陳冠希老師的潛質,更重要的是,每個人情況不一樣,就像深度學習一樣,訓練集效果很好,但測試集不行!
就撩妹而言,她會覺得你受前任(訓練集)影響很大,這是大忌!如果給她這個印象,你以后有的煩了,切記切記!
深度學習也是一個不斷磨合的過程,剛開始定義一個標準參數(這些是經驗值,就好比情人節和生日必須送花一樣),然后不斷地修正,得出圖 1 每個節點間的權重。
為什么要這樣磨合?試想一下,我們假設深度學習是一個小孩,我們怎么教他看圖識字?
肯定得先把圖片給他看,并且告訴他正確的答案,需要很多圖片,不斷地教他,訓練他,這個訓練的過程,其實就類似于求解神經網絡權重的過程。以后測試的時候,你只要給他圖片,他就知道圖里面有什么了。
所以訓練集,其實就是給小孩看帶有正確答案的圖片,對于深度學習而言,訓練集就是用來求解神經網絡的權重,最后形成模型;而測試集,就是用來驗證模型的準確度。
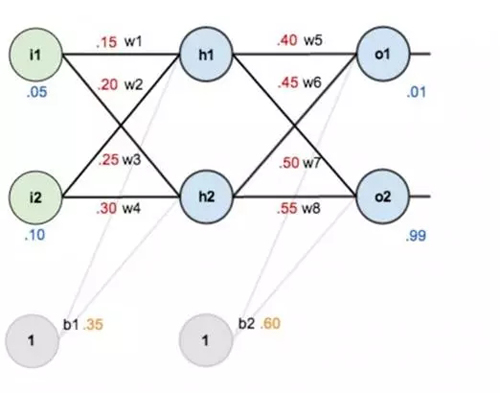
對于已經訓練好的模型,如下圖所示,權重(w1,w2...)都已知。
圖4
圖5
像上面這樣,從左至右容易算出來。但反過來,測試集有圖片,也有預期的正確答案,要反過來求 w1,w2......,怎么辦?
怎么求偏導數?
繞了半天,終于該求偏導出場了。目前的情況是:
我們假定一個神經網絡已經定義好,比如有多少層,每層有多少個節點,也有默認的權重和激活函數等。輸入(圖像)確定的情況下,只有調整參數才能改變輸出的值。怎么調整,怎么磨合?
每個參數都有一個默認值,我們就對每個參數加上一定的數值∆,然后看看結果如何?如果參數調大,差距也變大,那就得減小∆,因為我們的目標是要讓差距變小;反之亦然。
所以為了把參數調整到最佳,我們需要了解誤差對每個參數的變化率,這不就是求誤差對于該參數的偏導數嗎?
這里有兩個點:一個是激活函數,主要是為了讓整個網絡具有非線性特征。我們前面也提到了,很多情況下,線性函數沒辦法對輸入進行適當的分類(很多情況下識別主要是做分類)。
那么就要讓網絡學出來一個非線性函數,這里就需要激活函數,因為它本身就是非線性的,所以讓整個網絡也具有了非線性特征。
另外,激活函數也讓每個節點的輸出值在一個可控的范圍內,計算也方便。
貌似這樣解釋還是很不通俗,其實還可以用撩妹來打比方:女生都不喜歡白開水一樣的日子,因為這是線性的,生活中當然需要一些浪漫情懷了,這個激活函數嘛,我感覺類似于生活中的小浪漫,小驚喜。
相處的每個階段,需要時不時激活一下,制造點小浪漫,小驚喜。比如,一般女生見了可愛的小杯子,瓷器之類都邁不開步子,那就在她生日的時候送一個特別樣式,讓她感動得想哭。
前面講到男人要幽默,這是為了讓她笑,適當的時候還要讓她激動得哭。一哭一笑,多整幾個回合,她就離不開你了。因為你的非線性特征太強了。
當然,過猶不及,小驚喜也不是越多越好,但完全沒有就成白開水了。就好比每個 layer 都可以加激活函數,當然,不見得每層都要加激活函數,但完全沒有,那是不行的。
關鍵是怎么求偏導。圖 2 和圖 3 分別給了推導的方法,其實很簡單,從右至左挨個求偏導就可以。相鄰層的求偏導很簡單,因為是線性的,所以偏導數其實就是參數本身嘛,就跟求解 x₃ 的偏導類似。然后把各個偏導相乘就可以了。
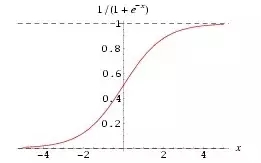
這里有兩個點:一個是激活函數,其實激活函數也沒啥,就是為了讓每個節點的輸出都在 0 到 1 的區間,這樣好算賬,所以在結果上面再做了一層映射,都是一對一的。
由于激活函數的存在,在求偏導的時候,也要把它算進去,激活函數,一般用 sigmoid,也可以用 Relu 等。激活函數的求導其實也非常簡單:
求導: f'(x)=f(x)*[1-f(x)]
這個方面,有時間可以翻看一下高數,如果沒時間,直接記住就行了。至于 Relu,那就更簡單了,就是 f(x) 當 x<0 的時候 y 等于 0,其他時候,y 等于 x。
當然,你也可以定義你自己的 Relu 函數,比如 x 大于等于 0 的時候,y 等于 0.01x,也可以。
什么是學習系數?
另一個是學習系數,為什么叫學習系數?
剛才我們上面講到∆增量,到底每次增加多少合適?是不是等同于偏導數(變化率)?
經驗告訴我們,需要乘以一個百分比,這個就是學習系數,而且,隨著訓練的深入,這個系數是可以變的。
當然,還有一些很重要的基本知識,比如 SGD(隨機梯度下降),mini batch 和 epoch(用于訓練集的選擇)。
上面描述的內容,主要是關于怎么調整參數,屬于初級階段。上面也提到,在調參之前,都有默認的網絡模型和參數,如何定義最初始的模型和參數?就需要進一步深入了解。
不過,對于一般做工程而言,只需要在默認的網絡上調參就可以,相當于使用算法;對于學者和科學家而言,他們會發明算法,這有很大的難度。向他們致敬!
【51CTO原創稿件,合作站點轉載請注明原文作者和出處為51CTO.com】