Generative Adversarial Network，就是大家耳熟能詳?shù)?GAN，由 Ian Goodfellow 首先提出，在這兩年更是深度學(xué)習(xí)中最熱門的東西，仿佛什么東西都能由 GAN 做出來。我最近剛?cè)腴T GAN，看了些資料，做一些筆記。

1.Generation

什么是生成（generation）？就是模型通過學(xué)習(xí)一些數(shù)據(jù)，然后生成類似的數(shù)據(jù)。讓機器看一些動物圖片，然后自己來產(chǎn)生動物的圖片，這就是生成。

以前就有很多可以用來生成的技術(shù)了，比如 auto-encoder（自編碼器），結(jié)構(gòu)如下圖：

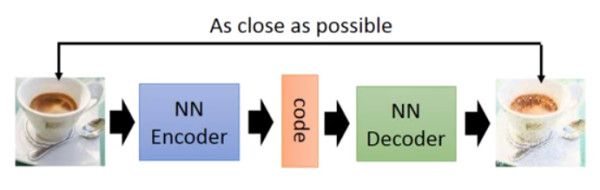
你訓(xùn)練一個 encoder，把 input 轉(zhuǎn)換成 code，然后訓(xùn)練一個 decoder，把 code 轉(zhuǎn)換成一個 image，然后計算得到的 image 和 input 之間的 MSE（mean square error），訓(xùn)練完這個 model 之后，取出后半部分 NN Decoder，輸入一個隨機的 code，就能 generate 一個 image。

但是 auto-encoder 生成 image 的效果，當然看著很別扭啦，一眼就能看出真假。所以后來還提出了比如VAE這樣的生成模型，我對此也不是很了解，在這就不細說。

上述的這些生成模型，其實有一個非常嚴重的弊端。比如 VAE，它生成的 image 是希望和 input 越相似越好，但是 model 是如何來衡量這個相似呢？model 會計算一個 loss，采用的大多是 MSE，即每一個像素上的均方差。loss 小真的表示相似嘛？

比如這兩張圖，***張，我們認為是好的生成圖片，第二張是差的生成圖片，但是對于上述的 model 來說，這兩張圖片計算出來的 loss 是一樣大的，所以會認為是一樣好的圖片。

這就是上述生成模型的弊端，用來衡量生成圖片好壞的標準并不能很好的完成想要實現(xiàn)的目的。于是就有了下面要講的 GAN。

2.GAN

大名鼎鼎的 GAN 是如何生成圖片的呢？首先大家都知道 GAN 有兩個網(wǎng)絡(luò)，一個是 generator，一個是 discriminator，從二人零和博弈中受啟發(fā)，通過兩個網(wǎng)絡(luò)互相對抗來達到***的生成效果。流程如下：

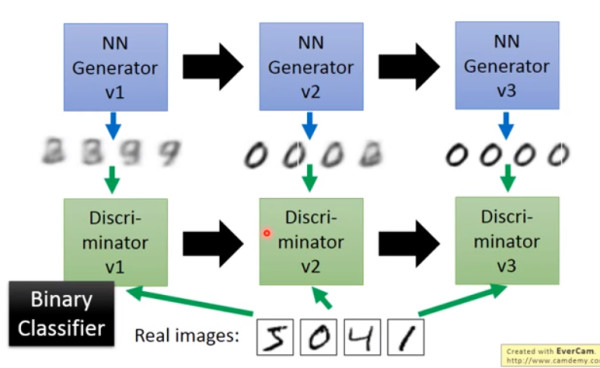
主要流程類似上面這個圖。首先，有一個一代的 generator，它能生成一些很差的圖片，然后有一個一代的 discriminator，它能準確的把生成的圖片，和真實的圖片分類，簡而言之，這個 discriminator 就是一個二分類器，對生成的圖片輸出 0，對真實的圖片輸出 1。

接著，開始訓(xùn)練出二代的 generator，它能生成稍好一點的圖片，能夠讓一代的 discriminator 認為這些生成的圖片是真實的圖片。然后會訓(xùn)練出一個二代的 discriminator，它能準確的識別出真實的圖片，和二代 generator 生成的圖片。以此類推，會有三代，四代。。。n 代的 generator 和 discriminator，*** discriminator 無法分辨生成的圖片和真實圖片，這個網(wǎng)絡(luò)就擬合了。

這就是 GAN，運行過程就是這么的簡單。這就結(jié)束了嘛？顯然沒有，下面還要介紹一下 GAN 的原理。

3.原理

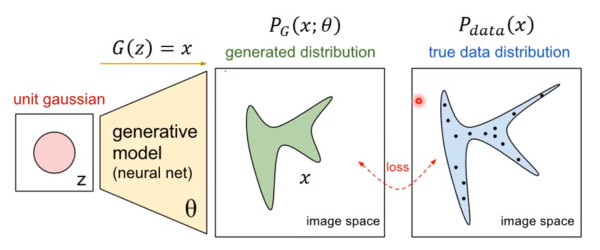
首先我們知道真實圖片集的分布 Pdata(x)，x 是一個真實圖片，可以想象成一個向量，這個向量集合的分布就是 Pdata。我們需要生成一些也在這個分布內(nèi)的圖片，如果直接就是這個分布的話，怕是做不到的。

我們現(xiàn)在有的 generator 生成的分布可以假設(shè)為 PG(x;θ)，這是一個由 θ 控制的分布，θ 是這個分布的參數(shù)（如果是高斯混合模型，那么 θ 就是每個高斯分布的平均值和方差）

假設(shè)我們在真實分布中取出一些數(shù)據(jù)，{x1, x2, ... , xm}，我們想要計算一個似然 PG(xi; θ)。

對于這些數(shù)據(jù)，在生成模型中的似然就是

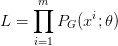
我們想要***化這個似然，等價于讓 generator 生成那些真實圖片的概率***。這就變成了一個***似然估計的問題了，我們需要找到一個 θ* 來***化這個似然。

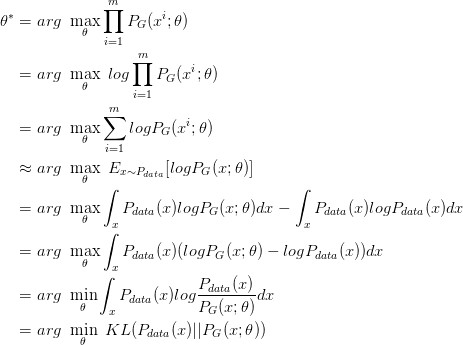
尋找一個 θ* 來***化這個似然，等價于***化 log 似然。因為此時這 m 個數(shù)據(jù)，是從真實分布中取的，所以也就約等于，真實分布中的所有 x 在 PG 分布中的 log 似然的期望。

真實分布中的所有 x 的期望，等價于求概率積分，所以可以轉(zhuǎn)化成積分運算，因為減號后面的項和 θ 無關(guān)，所以添上之后還是等價的。然后提出共有的項，括號內(nèi)的反轉(zhuǎn)，max 變 min，就可以轉(zhuǎn)化為 KL divergence 的形式了，KL divergence 描述的是兩個概率分布之間的差異。

所以***化似然，讓 generator ***概率的生成真實圖片，也就是要找一個 θ 讓 PG 更接近于 Pdata。

那如何來找這個最合理的 θ 呢？我們可以假設(shè) PG(x; θ) 是一個神經(jīng)網(wǎng)絡(luò)。

首先隨機一個向量 z，通過 G(z)=x 這個網(wǎng)絡(luò)，生成圖片 x，那么我們?nèi)绾伪容^兩個分布是否相似呢？只要我們?nèi)∫唤M sample z，這組 z 符合一個分布，那么通過網(wǎng)絡(luò)就可以生成另一個分布 PG，然后來比較與真實分布 Pdata。

大家都知道，神經(jīng)網(wǎng)絡(luò)只要有非線性激活函數(shù)，就可以去擬合任意的函數(shù)，那么分布也是一樣，所以可以用一直正態(tài)分布，或者高斯分布，取樣去訓(xùn)練一個神經(jīng)網(wǎng)絡(luò)，學(xué)習(xí)到一個很復(fù)雜的分布。

如何來找到更接近的分布，這就是 GAN 的貢獻了。先給出 GAN 的公式：

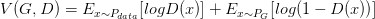
這個式子的好處在于，固定 G，max  V(G,D) 就表示 PG 和 Pdata 之間的差異，然后要找一個***的 G，讓這個***值最小，也就是兩個分布之間的差異最小。

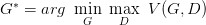
表面上看這個的意思是，D 要讓這個式子盡可能的大，也就是對于 x 是真實分布中，D(x) 要接近與 1，對于 x 來自于生成的分布，D(x) 要接近于 0，然后 G 要讓式子盡可能的小，讓來自于生成分布中的 x，D(x) 盡可能的接近 1。

現(xiàn)在我們先固定 G，來求解***的 D：

對于一個給定的 x，得到***的 D 如上圖，范圍在 (0,1) 內(nèi)，把***的 D 帶入

可以得到：

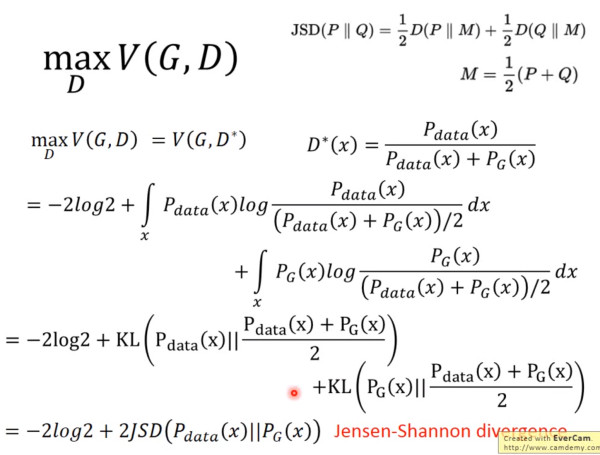
JS divergence 是 KL divergence 的對稱平滑版本，表示了兩個分布之間的差異，這個推導(dǎo)就表明了上面所說的，固定 G。

表示兩個分布之間的差異，最小值是 -2log2，***值為 0。

現(xiàn)在我們需要找個 G，來最小化

觀察上式，當 PG(x)=Pdata(x) 時，G 是***的。

4.訓(xùn)練

有了上面推導(dǎo)的基礎(chǔ)之后，我們就可以開始訓(xùn)練 GAN 了。結(jié)合我們開頭說的，兩個網(wǎng)絡(luò)交替訓(xùn)練，我們可以在起初有一個 G0 和 D0，先訓(xùn)練 D0 找到 ：

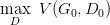
然后固定 D0 開始訓(xùn)練 G0， 訓(xùn)練的過程都可以使用 gradient descent，以此類推，訓(xùn)練 D1,G1,D2,G2,...

但是這里有個問題就是，你可能在 D0* 的位置取到了：

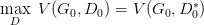
然后更新 G0 為 G1，可能

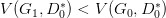
了，但是并不保證會出現(xiàn)一個新的點 D1* 使得

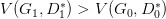
這樣更新 G 就沒達到它原來應(yīng)該要的效果，如下圖所示：

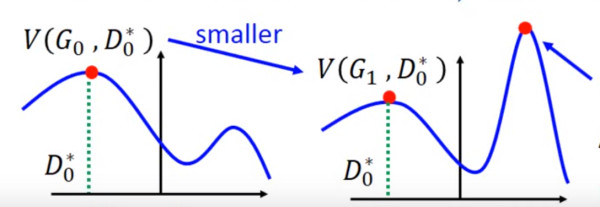
避免上述情況的方法就是更新 G 的時候，不要更新 G 太多。

知道了網(wǎng)絡(luò)的訓(xùn)練順序，我們還需要設(shè)定兩個 loss function，一個是 D 的 loss，一個是 G 的 loss。下面是整個 GAN 的訓(xùn)練具體步驟：

上述步驟在機器學(xué)習(xí)和深度學(xué)習(xí)中也是非常常見，易于理解。

5.存在的問題

但是上面 G 的 loss function 還是有一點小問題，下圖是兩個函數(shù)的圖像：

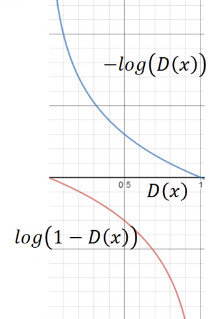
log(1-D(x)) 是我們計算時 G 的 loss function，但是我們發(fā)現(xiàn)，在 D(x) 接近于 0 的時候，這個函數(shù)十分平滑，梯度非常的小。這就會導(dǎo)致，在訓(xùn)練的初期，G 想要騙過 D，變化十分的緩慢，而上面的函數(shù)，趨勢和下面的是一樣的，都是遞減的。但是它的優(yōu)勢是在 D(x) 接近 0 的時候，梯度很大，有利于訓(xùn)練，在 D(x) 越來越大之后，梯度減小，這也很符合實際，在初期應(yīng)該訓(xùn)練速度更快，到后期速度減慢。

所以我們把 G 的 loss function 修改為

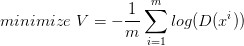
這樣可以提高訓(xùn)練的速度。

還有一個問題，在其他 paper 中提出，就是經(jīng)過實驗發(fā)現(xiàn)，經(jīng)過許多次訓(xùn)練，loss 一直都是平的，也就是

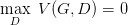
JS divergence 一直都是 log2，PG 和 Pdata 完全沒有交集，但是實際上兩個分布是有交集的，造成這個的原因是因為，我們無法真正計算期望和積分，只能使用 sample 的方法，如果訓(xùn)練的過擬合了，D 還是能夠完全把兩部分的點分開，如下圖：

對于這個問題，我們是否應(yīng)該讓 D 變得弱一點，減弱它的分類能力，但是從理論上講，為了讓它能夠有效的區(qū)分真假圖片，我們又希望它能夠 powerful，所以這里就產(chǎn)生了矛盾。

還有可能的原因是，雖然兩個分布都是高維的，但是兩個分布都十分的窄，可能交集相當小，這樣也會導(dǎo)致 JS divergence 算出來 =log2，約等于沒有交集。

解決的一些方法，有添加噪聲，讓兩個分布變得更寬，可能可以增大它們的交集，這樣 JS divergence 就可以計算，但是隨著時間變化，噪聲需要逐漸變小。

還有一個問題叫 Mode Collapse，如下圖：

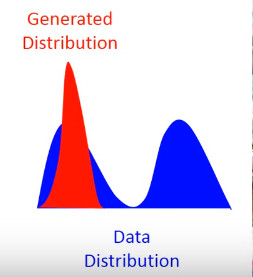
這個圖的意思是，data 的分布是一個雙峰的，但是學(xué)習(xí)到的生成分布卻只有單峰，我們可以看到模型學(xué)到的數(shù)據(jù)，但是卻不知道它沒有學(xué)到的分布。

造成這個情況的原因是，KL divergence 里的兩個分布寫反了

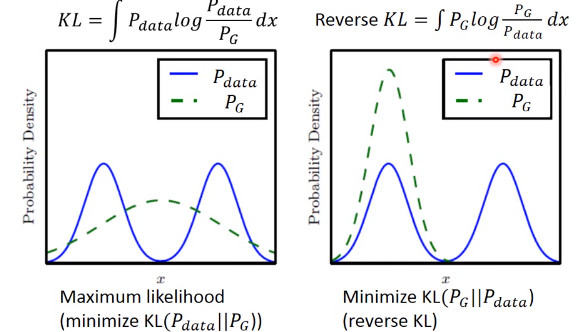
這個圖很清楚的顯示了，如果是***個 KL divergence 的寫法，為了防止出現(xiàn)無窮大，所以有 Pdata 出現(xiàn)的地方都必須要有 PG 覆蓋，就不會出現(xiàn) Mode Collapse。

6.參考

這是對 GAN 入門學(xué)習(xí)做的一些筆記和理解，后來太懶了，不想打公式了，主要是參考了李宏毅老師的視頻：

http://t.cn/RKXQOV0

本文轉(zhuǎn)自雷鋒網(wǎng)，本文作者馬少楠，原載于作者知乎專欄。