作為一個工科的學(xué)生,我們長期以來會使用比如像是矩陣以及行列式這些在線性代數(shù)上的知識,在這篇文章中,我想來聊一聊這些問題,即什么是面積,以及什么是面積的高緯度的推廣.

1 什么是面積?

對于什么是面積,大家可能首先就會想到我們生活中常用的長*寬么？真的是這樣么,其實在這里我們所談?wù)摰拿娣e,其實是歐幾里得空間幾何面積的基本的單位:平行四邊形的面積.關(guān)于平行四邊形的面積的定義,幾何上所說的就是相鄰兩邊邊長乘以他們之間的夾角的正弦.

但是當(dāng)我們面對到一些更一般的情形和更高維度的數(shù)理問題的時候,我們就有必要把這個面積的定義推廣開來.首先我們應(yīng)當(dāng)要注意的是.面積是作為一個標(biāo)量,他是來自于相鄰的兩個邊的兩個矢量相乘的結(jié)果,因此來時,我們需要把面積看作為一種映射的關(guān)系.

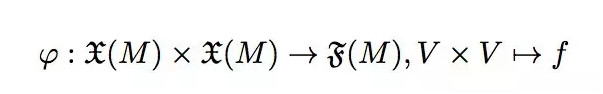
這里的V可以看做一個適量,V*V代表的是兩個適量的有序?qū)?那么f自然而然就是所求的面積.

現(xiàn)在我們將來證明這個映射是一個線性的映射,請坐穩(wěn)扶好:

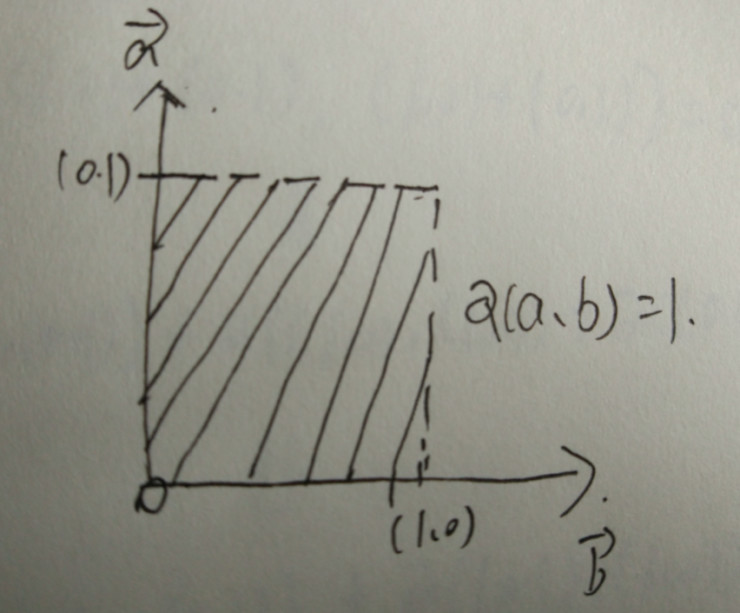
現(xiàn)在我們舉一個最簡單的例子,現(xiàn)在我們假設(shè)***個矢量是(1.0),第二個矢量是(0,1),也就是說兩個矢量分別是X軸和Y軸上的單位為正的單位向量,那么由這兩個矢量構(gòu)成的四邊形,這個四邊形其實就是一個正方形,根據(jù)面積的定義,其實就是*寬=1*1=1

因此我們可以得到:

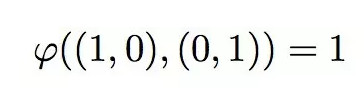
現(xiàn)在假設(shè)把***個矢量縮放a倍,這個四邊形的面積也會變?yōu)橄鄬?yīng)的a倍,這樣的面積也將會變?yōu)樵瓉淼腶倍,把第二個矢量縮放為b倍,這樣的面積也會變?yōu)樵瓉淼腷倍,如果這個時候我們同時對兩個向量縮放為ab倍,這樣的話面積也會變?yōu)樵瓉淼腶b倍,這說明,面積的映射對于其他的兩個操作數(shù)的矢量的標(biāo)量積是呈現(xiàn)出各自線性的,如下:

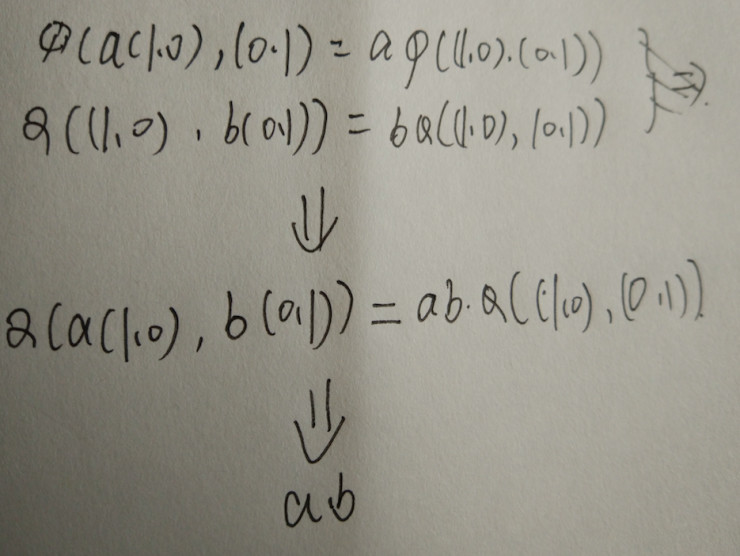
其實在實際的情況下,面積的映射對于其操作數(shù)(矢量)的矢量加法也是線性的.因為矢量加法的操作本身就是一個線性的,那么他的面積的映射其實也就是一個線性的映射.現(xiàn)在我想通過幾個例子,來解釋下映射加法線性的一些后果.

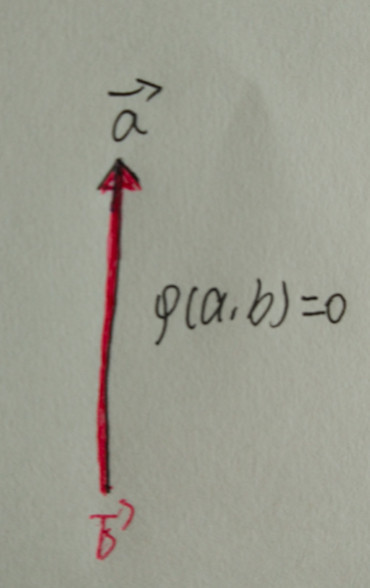
兩個共線矢量所張成的平行四邊形是一條線,因此來說這個面積是0.現(xiàn)在假設(shè)面積映射是關(guān)于一個適量加法的線性映射,那么我們有以下的結(jié)果

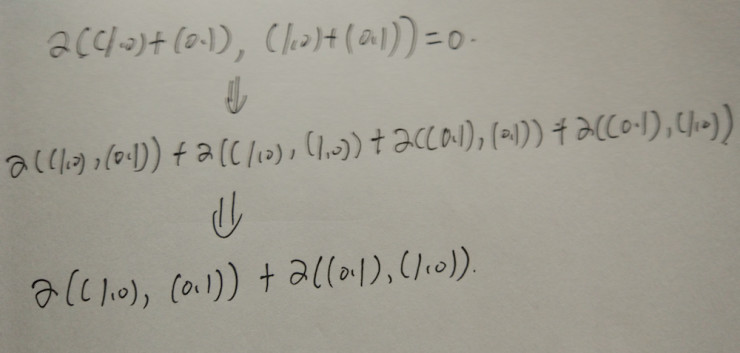
其實這里其實用到了一個理論:

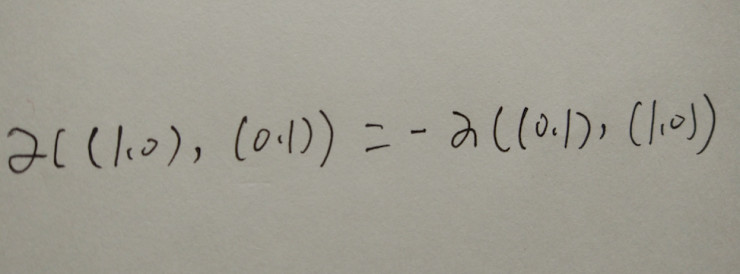
也就是說,在交換相互垂直操作數(shù)適量的順序后,面積的映射變成一個負(fù)值.到底是正還是負(fù)取決于你認(rèn)為的定義.一般情況下,我們把X軸的矢量放在前邊,Y軸的矢量放在后邊,從X軸到Y(jié)軸張成的一個平行四邊形的面積,我們把這個符號一般看作為正號.

2 三維空間里的應(yīng)用

在三維空間中,我們一般是利用的右手定則進(jìn)行實驗.如果以X軸的正方形為頭部,Y軸的正方向為尾部.右手定則告訴我,紙面方向向外的方向是面積的正方向.如果反過來,紙面向內(nèi)的方向就是該面積的正方向.與所規(guī)定的正負(fù)號的方向是相反的.現(xiàn)在這樣來看正負(fù)號的幾何的意義就比較明顯了

現(xiàn)在我們假設(shè)用平面內(nèi)的任意兩個矢量所張成的平行四邊形的面積,現(xiàn)在用公式來進(jìn)行表示:

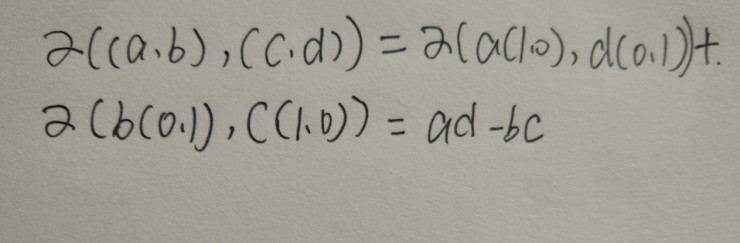
在這里,其實我們不難看到,所謂的面積其實就是一個2*2的矩陣的行列式:

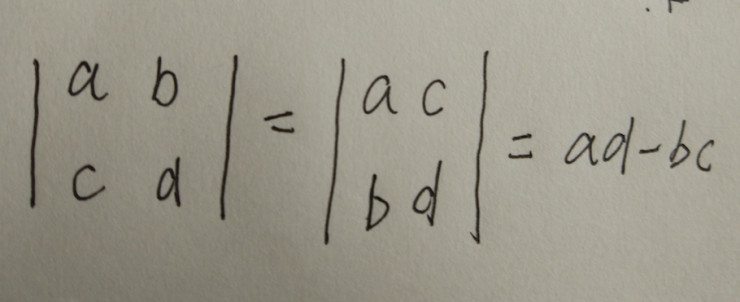
就跟下邊的圖所示的一樣:

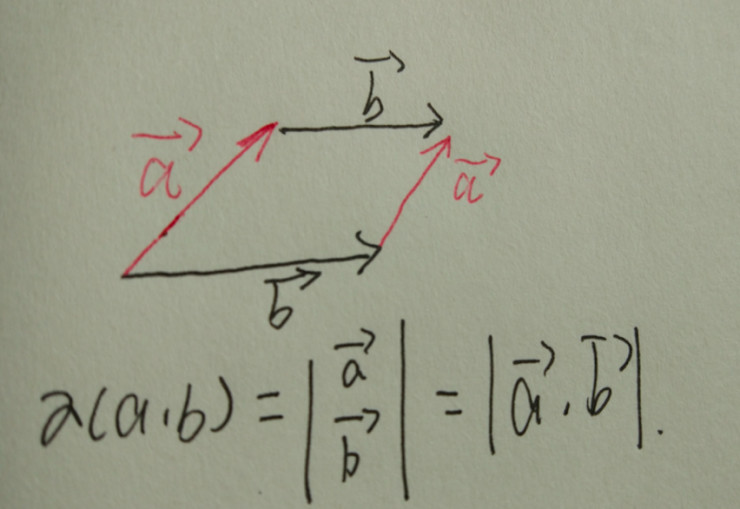
其實我們的***行即使我們的***個行向量(a,b),第二行就是第二個行向量(c,d),再或者是***列是***個列向量(a,b)的轉(zhuǎn)秩,第二個列自然就是第二個列向量(c,d)的轉(zhuǎn)秩.當(dāng)然這么做還是取決于我們是把矢量寫成行向量還是列向量的形式表達(dá).

3 行列式的性質(zhì)的計算

在上述的推理中,我們可以很容易的發(fā)現(xiàn),行列式的值是把與行列式的矢量寫成列向量的橫排還是行向量的豎排的方式是無關(guān)的.這也就是為什么,在計算行列式的時候,行列的地位是對等的.并且我們還應(yīng)當(dāng)注意到,根據(jù)上述的分析,交換向量的順序,面積是負(fù)號的原因.這也就是為什么行列式中,交換列向量或者行向量一次,就應(yīng)當(dāng)要取一次負(fù)號的原因.另外行列式其他的計算的性子,其實都一一反映在面積映射的線性性當(dāng)中.

所以,綜上所述,行列式實際上本身就是一個關(guān)于面積的形式的推廣.其實就是在給定一組基的情況下,N個向量張成的一個N維定義的廣義四邊形的體積,其實這就是行列式本質(zhì)的一個含義.

4 行列式的一個推廣

根據(jù)上邊的結(jié)論,我們其實很容易的推廣到三維體積的一個計算:

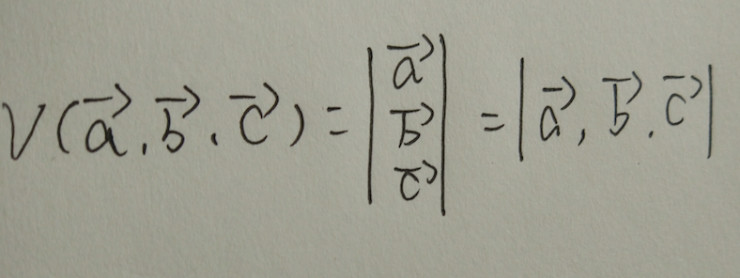
在這里我們應(yīng)該要注意到,行列式的定義,其實是每一行各取一個不同列的元素的一個乘積并且符號和所謂的逆序性有關(guān)的.什么是逆虛性?所謂逆序性，其幾何意義就是在規(guī)定了一個正方向之后（比如從1,2,3,4,5...N這個順序定義為正號），交換任意一對數(shù)都取一次負(fù)號。這樣的性質(zhì)我們在上述的面積函數(shù)中已經(jīng)有所看到，實際上體積，更高維度的廣義體積，也有正方向之說，只不過已經(jīng)難以用右手法則（以及叉乘）來形象說明罷了。右手定則的局限性也是將高維面積推廣成行列式表達(dá)的一個動機(jī)之一。

對于這樣交換任意一堆指標(biāo)的操作就可以改變符號的性質(zhì),其實我們就叫做反對稱性.這個時候,如果你善于思考,你會想為什么要取不同行不同列元素的乘積.因為如果有任意兩個元素是同行同列的,那么他們交換他們的列指標(biāo),乘積不變但是符號要相反.因此乘積必須要是0,這也就是在行列式值中不予體現(xiàn)的原因之一.

行列式的定義其實是比較的冗雜的,其實就是來自于廣大的面積映射的反對稱性,其實面積映射是一個2維的,把二維任意拓展到多維,我們其實就可以發(fā)現(xiàn)R維的形式和R*R的行列式的形式是完全一致的.

其實在這里,我們可以把各種維度所代表的東西來總結(jié)下,二維所代表的是平面內(nèi)的面積,三維自然而然其實就是三維空間內(nèi)的體積,四維其實就是四維空間內(nèi)的超體積.依次類推.在上邊的推理中我們發(fā)現(xiàn),這些矢量給定的基坐標(biāo)寫出的矩陣必然是方陣,矩陣的行列式對應(yīng)的面積或者是體積.這樣的推廣證明相信在任意一本的線性代數(shù)書中都會看到,我只是說了人話而已.

5 行列式和矩陣的逆

我們知道很多定理,比如行列式為0的矩陣,不可逆,行列式不為0的矩陣,可逆,這個時候我們不禁要問,代表面積的行列式,是如何和線性變化的可逆性聯(lián)合在一起的.

這個時候我們就應(yīng)該要理解線性變化的幾何意義.現(xiàn)在我來陳述一下:

如果我們把空間中一組線性無關(guān)的矢量都寫成列向量的形式，那么他們所張成的N維體體積不為零，根據(jù)上面的分析，其值由行列式給出。向量經(jīng)過線性變換A變換之后，得到的新向量形式如下：

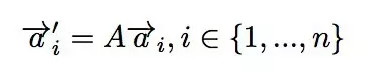
注意到A是一個N*N的矩陣，向量是列向量。

變換前，N維體的體積是：

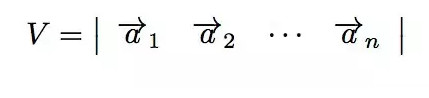
變換之后，N維體的體積是（注意到，第二個等式實際上說明了幾何意義是如何定義矩陣乘法的，也就是N*N矩陣A和另外一個N個列向量組成的N*N矩陣的乘法）：

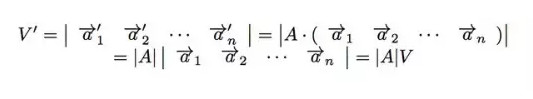
A的行列式如果不為零，則代表這個變換后，N維體的體積不是NULL。又結(jié)合線性無關(guān)與體積的性質(zhì)，我們可以說：

如果A的行列式不為零，那么A可以把一組線性無關(guān)的矢量，映射成一組新的，線性無關(guān)的矢量；A是可逆的（一對一的映射，保真映射，KERNEL是{0}）

如果A的行列式為零，那么A就會把一組線性無關(guān)的矢量，映射成一組線性相關(guān)的矢量

如果A的行列式為負(fù)數(shù)，那么A將會改變原N維體體積的朝向。

從線性無關(guān)到線性相關(guān)，其中丟失了部分信息（例如坍縮成共線或者共面），因此這個變換顯然就是不可逆的。線性是否無關(guān)和所張成N維體的體積有直接關(guān)系，這個體積值又與A的行列式有關(guān)。因此我們就建立了A的行列式與其是否可逆的幾何關(guān)系。

舉例說明，我們假設(shè)A是一個3維的矩陣。如果映射前，有一組三個線性無關(guān)的矢量，我們知道它們張成的體積不是0；經(jīng)過映射后，他們對應(yīng)的新矢量也能張成一個平行六面體，那么這個平行六面體的體積就是原體積乘以A的行列式。

顯然，如果A的行列式是0，那么變換后的新“平行六面體"的體積將不可避免的也是0。根據(jù)上文的結(jié)論，我們有：變換后的這一組新矢量線性相關(guān)。

結(jié)論：

線性變換A的行列式是否為零，就代表了其映射的保真性，也即，能不能把一組線性無關(guān)的矢量變換成另一組保持無關(guān)性的矢量。

6 秩

但是有的時候,雖然行列式A不能把空間一組數(shù)目***的矢量線性無關(guān),但是它能夠保證那個一組少數(shù)目的矢量讓其線性無關(guān),這個數(shù)目矢量往往小于線性空間的維度,這個數(shù)目就叫做線性變換A的秩

比如:一個秩為2為3*3的矩陣A,因為秩小于3,那么任何一個3維六面體經(jīng)過他的變化后,體積變?yōu)?,退化一個面,但是仍然存在一個面積不為0的面,在變換以后還是一個非零面積的面

所以說所謂的一個線性變換的秩,無非就是變化后,還能保持一個非零體積的幾何形狀的***的維度.

通過上邊理解了秩,行列式,可逆性的幾何意義,我們就能隨意的構(gòu)造一個線性變化的A,使得他要么保全所有的幾何體,要么降維成為特定維度特定結(jié)構(gòu)的幾何體,壓縮成為更低維度的幾何體,所以說,可以看作為一個”降維打擊”

更高維度的推理,希望有興趣的小伙伴可以自己去證明,不明白的問題亦可以在文章下面評論.希望能夠和大家多多交流,多謝指教.

本文轉(zhuǎn)自雷鋒網(wǎng)，如需轉(zhuǎn)載請至雷鋒網(wǎng)官網(wǎng)申請授權(quán)。本文作者夏洪進(jìn)，原載于作者的個人博客。