上一次我們說完了用 HashSet 來進行計數(shù)了。我們可以發(fā)現(xiàn)，如果我們估計有N個數(shù)，那么我們至少需要N*32bit(按照int在32位操作系統(tǒng)下占用32個bit)的空間來進行存儲，這太費錢了。有沒有辦法進行改進呢?這就引出了一個新的數(shù)據(jù)結(jié)構(gòu) - BitMap。

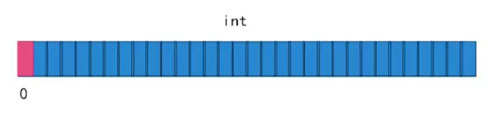
這時候看到一張圖代表了一個存儲int的字節(jié)bit信息。

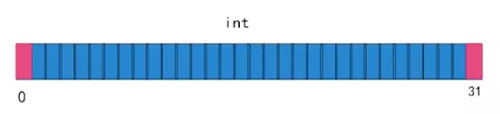
我們可以發(fā)現(xiàn)，每一個bit都有自己的值，比如一個int的空間除了作為int類型的數(shù)字外，是否還可以做其他的利用?數(shù)字可以表示0~31位置的情況，如果我們使用bit的位置信息來存儲會怎樣?我們來試試看。

如果我們得到Hash的值為0，那就直接將第0位置上的bit位置為1。

如果我們得到Hash的值為31，那就直接將第31上的bit位置為1。

如果發(fā)現(xiàn)位置上已經(jīng)有值了，那當(dāng)前的值就已經(jīng)存在了，不再進行統(tǒng)計，這樣子就可以完成超大數(shù)據(jù)量的統(tǒng)計啦。

這樣進行存儲的數(shù)據(jù)結(jié)構(gòu)就叫BitMap，使用每個bit位來進行信息存儲，而不是一個int數(shù)字。

那有小伙伴就有疑問了，如果超過了32個數(shù)字怎么辦?

可以使用數(shù)組來進行拓展，比如一個a = int[2]的數(shù)組。

a[0] 可以表示0~31位，a[1] 可以表示32~63位，以此類推，幾乎可以***大。如果數(shù)據(jù)確實非常巨大，連下標也到達int的界限了，也可以用其他的單個空間更大的數(shù)據(jù)類型來進行存儲。

相比較于HashSet，BitMap 進行統(tǒng)計所使用的存儲只需要 HashSet 的1/32。但是這個數(shù)據(jù)結(jié)構(gòu)簡單，相對于 HashSet 有一點小問題，就是hash在數(shù)據(jù)量巨大的情況下，碰撞會比較嚴重，那么統(tǒng)計精度會下降，需要怎么改善呢?請關(guān)注下一篇布隆過濾器。

【本文為51CTO專欄作者“大蕉”的原創(chuàng)稿件，轉(zhuǎn)載請通過作者微信公眾號“一名叫大蕉的程序員”獲取授權(quán)】

戳這里，看該作者更多好文