數據挖掘領域十大經典算法之—K-Means算法(超詳細附代碼)
k-means算法比較簡單。在k-means算法中,用cluster來表示簇;容易證明k-means算法收斂等同于所有質心不再發生變化。基本的k-means算法流程如下:
簡介
又叫K-均值算法,是非監督學習中的聚類算法。
基本思想
k-means算法比較簡單。在k-means算法中,用cluster來表示簇;容易證明k-means算法收斂等同于所有質心不再發生變化。基本的k-means算法流程如下:
選取k個初始質心(作為初始cluster,每個初始cluster只包含一個點);
repeat:
- 對每個樣本點,計算得到距其最近的質心,將其類別標為該質心所對應的cluster;
- 重新計算k個cluster對應的質心(質心是cluster中樣本點的均值);
- until 質心不再發生變化 12345
repeat的次數決定了算法的迭代次數。實際上,k-means的本質是最小化目標函數,目標函數為每個點到其簇質心的距離的平方和:
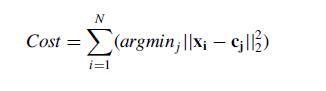
- N是元素個數,x表示元素,c(j)表示第j簇的質心
- 算法復雜度
- 時間復雜度是O(nkt) ,其中n代表元素個數,t代表算法迭代的次數,k代表簇的數目
優缺點
- 優點
- 簡單、快速;
- 對大數據集有較高的效率并且是可伸縮性的;
- 時間復雜度近于線性,適合挖掘大規模數據集。
缺點
- k-means是局部***,因而對初始質心的選取敏感;
- 選擇能達到目標函數***的k值是非常困難的。
代碼
代碼已在github上實現,這里也貼出來
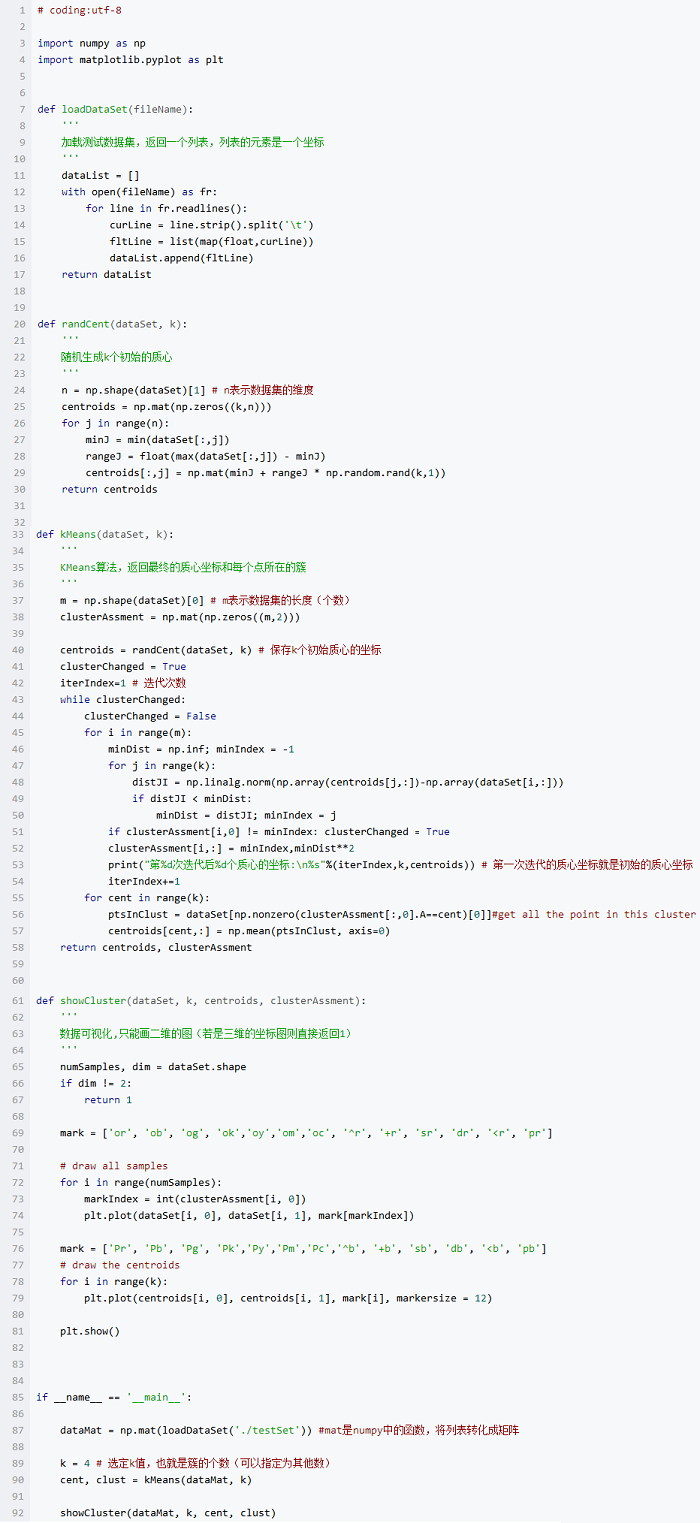
測試數據集獲取地址為testSet