成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看

20張圖帶你搞懂十大經典排序算法

作者：李立敏
開發 前端 算法
在面試的過程中經常會遇到手寫排序算法，所以本文就簡單總結一下。不對算法的細節做介紹，只做一個概括性的描述。

[[433768]]

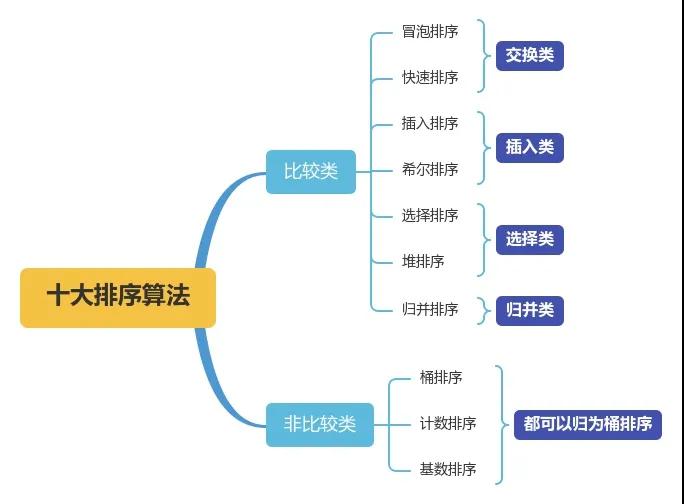
十大排序算法思路匯總

在面試的過程中經常會遇到手寫排序算法，所以本文就簡單總結一下。不對算法的細節做介紹，只做一個概括性的描述。

交換類：通過元素之間的兩兩交換來實現排序

插入類：將數分為2部分，依次將無序的數插入到有序的數列中

選擇類：從待排序數列中找到最小值或者最大值元素，放到已拍好序的序列后面

「計數排序和基數排序可以認為是桶排序的一種特殊實現，都不是通過元素之間的比較來實現排序的」

冒泡排序

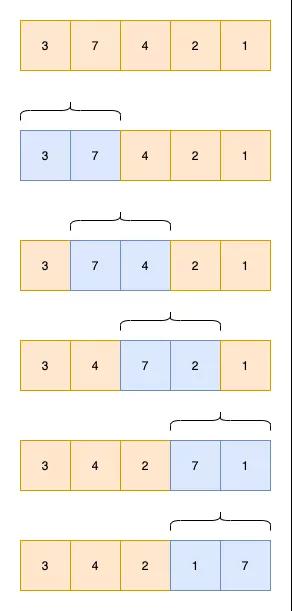
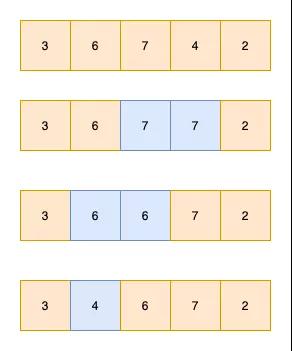
冒泡排序，從頭開始，依次比較數組中相鄰的2個元素，如果后面的數比前面的數大，則交換2個數，否則不交換。每進行一輪比較，都會把數組中最大的元素放到最后面。

如下圖，一輪比較的過程如下

當數組中有n個元素時，只需要進行n輪比較，則整個數組就是有序的

  1. public static void bubbleSort(int[] a) { 
  2.  // 進行i輪比較 
  3.     for (int i = 0; i < a.length - 1; i++) { 
  4.         for (int j = 0; j < a.length - 1 - i; j++) { 
  5.             if (a[j] > a[j + 1]) { 
  6.                 swap(a, j, j + 1); 
  7.             } 
  8.         } 
  9.     } 
  10. } 
  11.  
  12. public static void swap(int[] a, int i, int j) { 
  13.     int temp = a[i]; 
  14.     a[i] = a[j]; 
  15.     a[j] = temp; 
  16. } 

快速排序

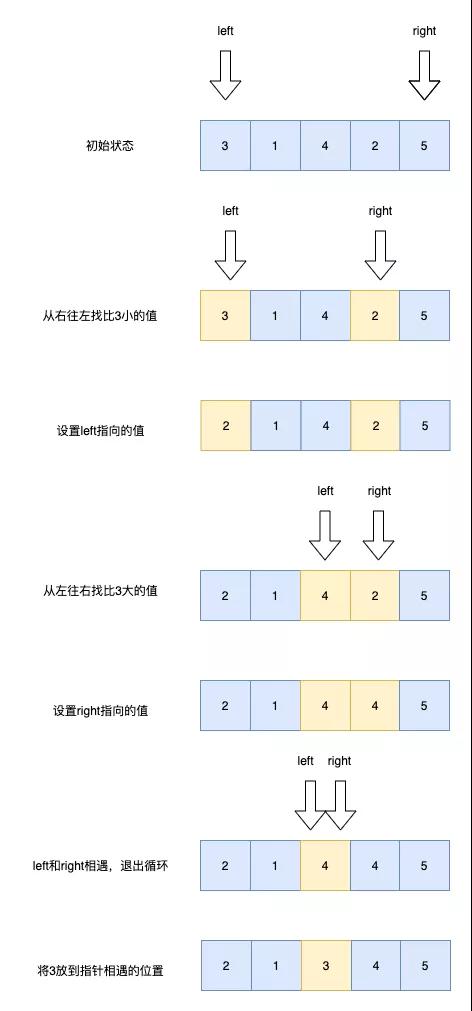
快速排序的執行流程主要分為如下三步

從數列中取出一個數作為基準數

分區，將比它大的數全放到它的右邊，小于或等于它的數全放到它的左邊

再對左右區間重復第二步，直到各區間只有一個數

  1. public static void quickSort(int[] a, int left, int right) { 
  2.     if (left >= right) { 
  3.         return; 
  4.     } 
  5.     int index = sort(a, left, right); 
  6.     quickSort(a, left, index - 1); 
  7.     quickSort(a, index + 1, right); 
  8. } 
  9.  
  10. public static int sort(int[] a, int left, int right) { 
  11.     int key = a[left]; 
  12.     while (left < right) { 
  13.         // 從high所指位置向前搜索找到第一個關鍵字小于key的記錄和key互相交換 
  14.         while (left < right && a[right] >= key) { 
  15.             right--; 
  16.         } 
  17.         a[left] = a[right]; 
  18.         // 從low所指位置向后搜索，找到第一個關鍵字大于key的記錄和key互相交換 
  19.         while (left < right && a[left] <= key) { 
  20.             left++; 
  21.         } 
  22.         a[right] = a[left]; 
  23.     } 
  24.     // 放key值，此時left和right相同 
  25.     a[left] = key; 
  26.     return left; 
  27. } 

下圖演示了一次分區的流程

「經典的Top K面試題一般就可以用快排和堆排序來解決」。我們在下一節手寫堆排序來分析吧

插入排序

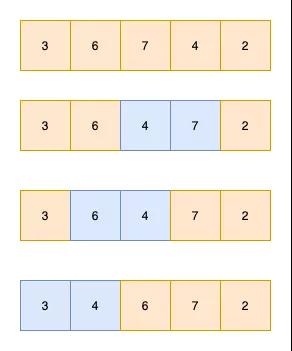
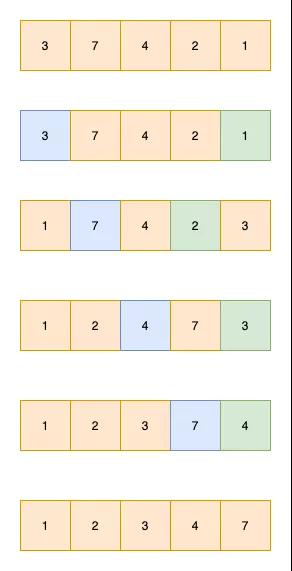
將數組分為2端，有序數組和無序數組，依次將無序數組中的值插入到無序數組中。

如下圖3 6 7為有序數組，4 2為無序數組。依次將4，2插入到無序數組中即可

如圖，插入4的過程如下

程序怎么劃分有序數組和無序數組呢?可以認為第一個元素為有序數組，后面的值依次插入即可

  1. public static void insertionSort(int[] a) { 
  2.     for (int i = 1; i < a.length; i++) { 
  3.         for (int j = i; j > 0; j--) { 
  4.             while (a[j] < a[j - 1]) { 
  5.                 swap(a, j, j - 1); 
  6.             } 
  7.         } 
  8.     } 
  9. } 
  10.  
  11. public static void swap(int[] a, int i, int j) { 
  12.     int temp = a[i]; 
  13.     a[i] = a[j]; 
  14.     a[j] = temp; 
  15. } 

「可以看到有很多無用的交換位置的過程，我們可以先直接定位到要交換的元素，然后進行一次交換即可。改進后的插入排序代碼」

  1. public static void insertionSort(int[] a) { 
  2.     for (int i = 1; i < a.length; i++) { 
  3.         int temp = a[i]; 
  4.         int j; 
  5.         // 查到合適的插入位置，插入即可 
  6.         for (j = i - 1; j >= 0 && a[j] > temp; j--) { 
  7.             a[j + 1] = a[j]; 
  8.         } 
  9.         a[j + 1] = temp; 
  10.     } 
  11. } 

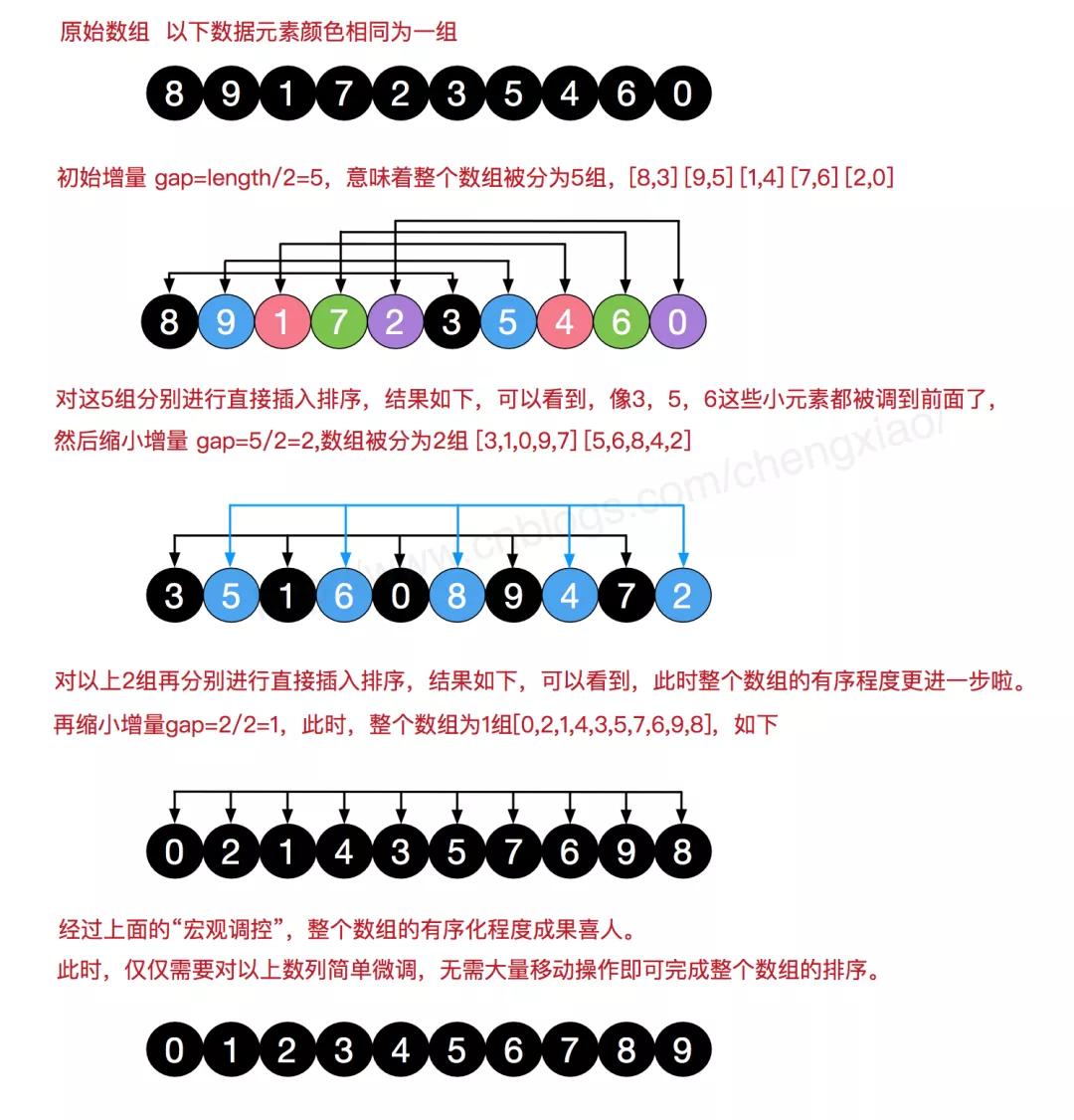
希爾排序

「希爾排序是基于插入排序改進后的算法。因為當數據移動次數太多時會導致效率低下。所以我們可以先讓數組整體有序(剛開始移動的幅度大一點，后面再小一點)，這樣移動的次數就會降低，進而提高效率」

原文地址：博客園《圖解排序算法(二)之希爾排序》

  1. public static void shellSort(int[] a) { 
  2.     for (int step = a.length / 2; step > 0; step /= 2) { 
  3.         for (int i = step; i < a.length; i++) { 
  4.             int temp = a[i]; 
  5.             int j; 
  6.             for (j = i - step; j >= 0 && a[j] > temp ; j -= step) { 
  7.                 a[j + step] = a[j]; 
  8.             } 
  9.             a[j + step] = temp; 
  10.         } 
  11.     } 
  12. } 

選擇排序

第一次迭代，將最小的放在數組第0個位置 第二次迭代，將次小的放在數組第1個位置

  1. public static void selectionSort(int[] a) { 
  2.     for (int i = 0; i < a.length; i++) { 
  3.         int index = i; 
  4.         for (int j = i + 1; j < a.length; j++) { 
  5.             if (a[index] > a[j]) { 
  6.                 index = j; 
  7.             } 
  8.         } 
  9.         if (index != i) { 
  10.             swap(a, index, i); 
  11.         } 
  12.     } 
  13. } 
  14.  
  15. public static void swap(int[] a, int i, int j) { 
  16.     int temp = a[i]; 
  17.     a[i] = a[j]; 
  18.     a[j] = temp; 
  19. } 

堆排序

我們來手寫一下堆排序，首先我們解釋一下什么是堆?

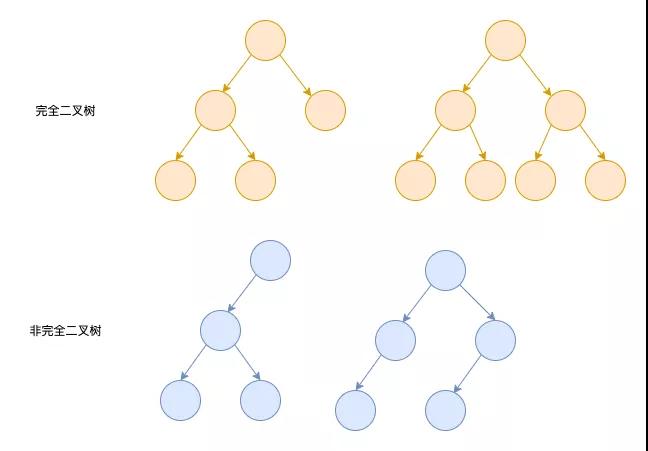
  1. 堆是一種數據結構，需要滿足如下幾個特性
  2. 堆是一顆完全二叉樹(生成節點的順序是從左往右，從上往下依次進行)

堆中某個節點值總是不大于或者不小于其父節點的值

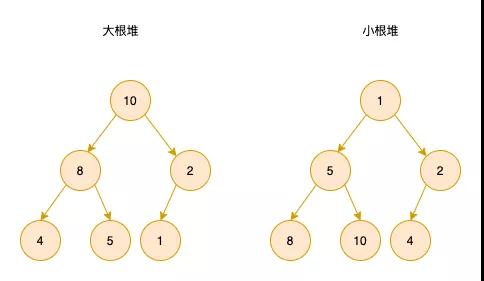
「將根結點最大的堆叫做最大堆或大根堆，根結點最小的堆叫做最小堆或小根堆」

大根堆和小根堆如下圖所示

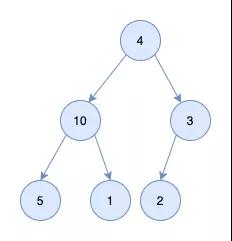
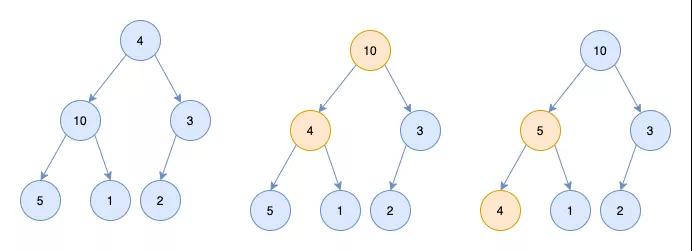
假設有如下一個完全二叉樹，如何將它調整為一個堆呢?

可以看到10及其子節點符合條件，3及其子節點符合條件，4這個節點不符合條件。

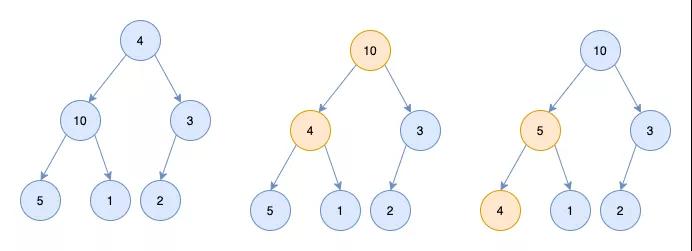
「所以要對4這個節點進行調整，調整的過程稱為heapify」

  • 從4這個節點的左右節點找一個大的節點(即10這個節點)和4這個節點進行交換
  • 交換完有可能交換后的節點不符合條件，所以還需要進行調整(調整過程和1類似)
  • 最終4節點和5節點進行交換。二叉樹變為堆

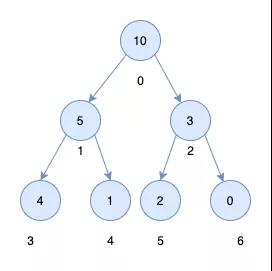
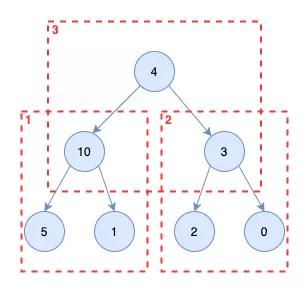
在實際開發的過程中，我們并不會用樹這種結構來表示堆，而是用數組。通過下標的特點，可以總結出如下規律

假如一個節點在數組中的節點下標為i，則

父節點下標為：parent = (i - 1) / 2 左節點下標為：c1 = 2 * i + 1 右節點下標為：c2 = 2 * i + 2

所以上圖中的堆，用數組表示為[10, 5, 3, 4, 1, 2, 0]

知道了如何用數組表示堆，我們寫一下對如下4這個節點heapify的過程

  1. /** 
  2.  * @param a 數組 
  3.  * @param n 數組長度 
  4.  * @param i 要進行heapify的節點 
  5.  */ 
  6. public static void heapify(int[] a, int n, int i) { 
  7.     // 遞歸出口 
  8.     if (i >= n) { 
  9.         return; 
  10.     } 
  11.     // 左節點下標 
  12.     int c1 = 2 * i + 1; 
  13.     // 右節點下標 
  14.     int c2 = 2 * i + 2; 
  15.     int max = i; 
  16.     if (c1 < n && a[c1] > a[max]) { 
  17.         max = c1; 
  18.     } 
  19.     if (c2 < n && a[c2] > a[max]) { 
  20.         max = c2; 
  21.     } 
  22.     // 將左節點，右節點中的最大值和父節點交換 
  23.     if (max != i) { 
  24.         swap(a, max ,i); 
  25.         heapify(a, n, max); 
  26.     } 
  27. } 
  1. @Test 
  2. public void heapify() { 
  3.     int[] array = new int[]{4, 10, 3, 5, 1, 2}; 
  4.     // 調整后為 10， 5， 3， 4， 1， 2 
  5.     HeapSort.heapify(array, array.length,0); 

「我們如何把一個完全二叉樹變為堆呢?」

「只要對非葉子節點從左邊往右，從下到上依次進行heapify即可。」 如下圖只需要依次對10，3，4進行heapify即可

  1. public static void buildTree(int[] a) { 
  2.     // 找到最后一個非葉子節點 
  3.     int lastNode = a.length - 1; 
  4.     int parent = (lastNode - 1) / 2; 
  5.     for (int i = parent; i >= 0; i--) { 
  6.         heapify(a, a.length, i); 
  7.     } 
  8. } 

我們來測試一下

  1. @Test 
  2. public void buildTree() { 
  3.     int[] array = new int[]{3, 5, 7, 2, 4, 9, 6}; 
  4.     // 9 5 7 2 4 3 6 
  5.     HeapSort.buildTree(array); 
  6. } 

知道了堆是如何生成以及如何調整的過程，我們再分析堆排序的過程就非常簡單了!

以大頂堆為例，最大值一定是根節點。

  1. 將根節點和最后一個葉子節點交換，然后將這個葉子節點移出堆
  2. 此時根節點是不符合要求的，所以對根節點進行heapify后，又變成了一個堆了
  3. 重復1，2步，就能找出剩余節點中的最大值

因為每次找出的最大值，都是在數組的最后一位，所以我們不需要真正的進行移除堆這個操作，只是進行heapify的時候，數組長度逐漸遞減即可。最終的數組就是升序的

  1. public static void heapSort(int[] a) { 
  2.     // 先構建一個堆 
  3.     buildTree(a); 
  4.     // 每次將堆的根節點和最后一個節點進行交換，然后進行heapify 
  5.     for (int i = a.length - 1; i >= 0; i--) { 
  6.         swap(a, i, 0); 
  7.         heapify(a, i, 0); 
  8.     } 
  9. } 

所以最終一個堆排序的代碼如下

  1. public class HeapSort { 
  2.  
  3.     public static void heapSort(int[] a) { 
  4.         buildTree(a); 
  5.         for (int i = a.length - 1; i >= 0; i--) { 
  6.             swap(a, i, 0); 
  7.             heapify(a, i, 0); 
  8.         } 
  9.     } 
  10.  
  11.     public static void buildTree(int[] a) { 
  12.         // 找到最后一個非葉子節點 
  13.         int lastNode = a.length - 1; 
  14.         int parent = (lastNode - 1) / 2; 
  15.         for (int i = parent; i >= 0; i--) { 
  16.             heapify(a, a.length, i); 
  17.         } 
  18.     } 
  19.  
  20.     /** 
  21.      * @param a 數組 
  22.      * @param n 數組長度 
  23.      * @param i 要進行heapify的節點 
  24.      */ 
  25.     public static void heapify(int[] a, int n, int i) { 
  26.         if (i >= n) { 
  27.             return; 
  28.         } 
  29.         int c1 = 2 * i + 1; 
  30.         int c2 = 2 * i + 2; 
  31.         int max = i; 
  32.         if (c1 < n && a[c1] > a[max]) { 
  33.             max = c1; 
  34.         } 
  35.         if (c2 < n && a[c2] > a[max]) { 
  36.             max = c2; 
  37.         } 
  38.         if (max != i) { 
  39.             swap(a, max ,i); 
  40.             heapify(a, n, max); 
  41.         } 
  42.     } 
  43.  
  44.     public static void swap(int[] a, int i, int j) { 
  45.         int temp = a[i]; 
  46.         a[i] = a[j]; 
  47.         a[j] = temp; 
  48.     } 
  49. } 

我們這里只演示了一下如何構建一個堆，以及堆排序的流程是怎樣的?

「要實現一個完整的堆，我們還需要提供一個插入節點和刪除根節點的方法」。我就不寫實現了，用圖演示一下流程，有興趣的可以寫一下，「大部分語言都會內置堆的實現，即優先級隊列(Java中為PriorityQueue)，所以當我們有用到堆的場景時，直接用PriorityQueue即可」

堆插入節點

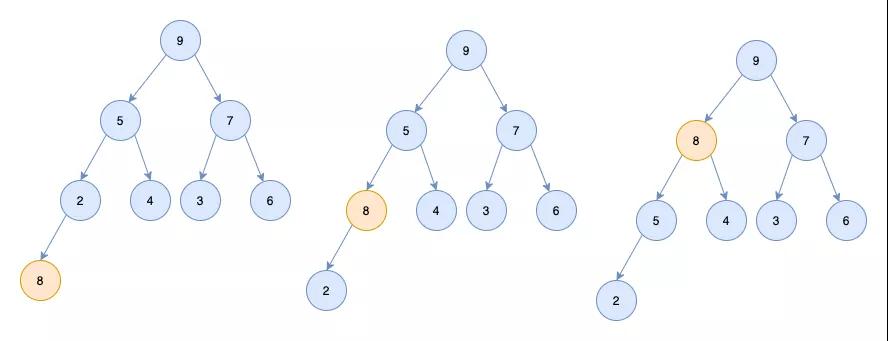
當堆插入節點時，插入的位置是完全二叉樹的最后一個位置。比如我們插入一個新節點，值是8

我們讓8和它的父節點比較，8>5，則讓新節點上浮，和父節點交換位置

交換完后繼續和父節點比較，8<9，則不用調整了

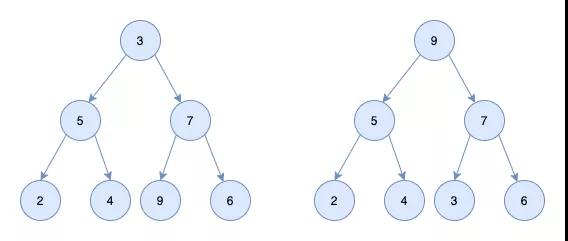
堆刪除節點

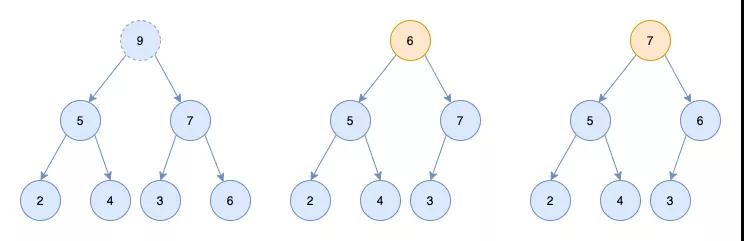
堆刪除節點時，刪除的是堆頂的節點。比如我們刪除大頂堆的9節點

為了維持堆的結構，我們把堆的最后一個節點6補到堆頂的位置

接著我們讓堆頂的節點和它的左右孩子節點進行比較，如果左右孩子中最大的一個比節點6大，那么則讓節點6下沉

接著和左右節點進行比較，3<6，則不用調整了

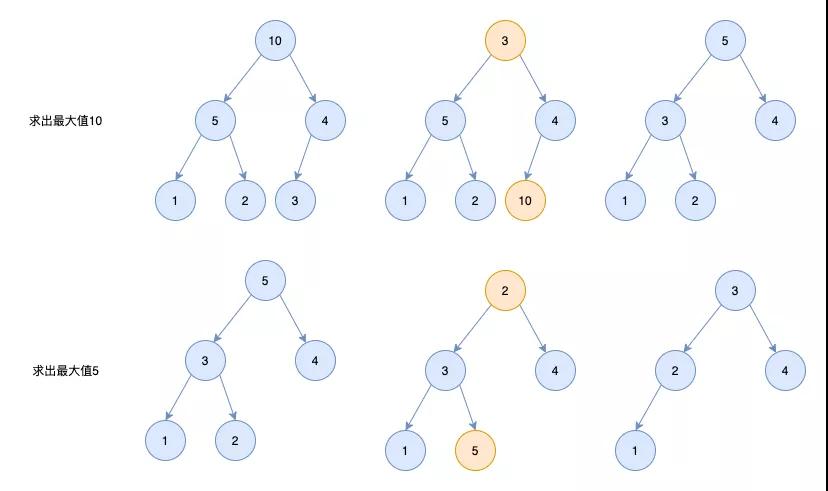
前 K 個高頻元素

題目地址：劍指 Offer 40. 最小的k個數

輸入整數數組 arr ，找出其中最小的 k 個數。例如，輸入4、5、1、6、2、7、3、8這8個數字，則最小的4個數字是1、2、3、4。

  1. 輸入：arr = [3,2,1], k = 2 
  2. 輸出：[1,2] 或者 [2,1] 

限制：

0 <= k <= arr.length <= 10000 0 <= arr[i] <= 10000

「堆」

維護一個大頂堆 當堆中的元素不夠k時，一直往堆中放元素即可 當堆中的元素大于等于k時，將堆頂的元素和新添加的元素進行比較。如果新添的元素比堆頂的元素小，則應該把堆頂的元素刪除，將新填的元素放入堆，這樣就能保證堆中的元素一直是最小的k個

  1. public int[] getLeastNumbers(int[] arr, int k) { 
  2.     if (arr.length == 0 || k == 0) { 
  3.         return new int[0]; 
  4.     } 
  5.     PriorityQueue<Integer> queue = new PriorityQueue<>((num1, num2) -> num2 - num1); 
  6.     for (int num : arr) { 
  7.         if (queue.size() < k) { 
  8.             queue.add(num); 
  9.         } else if (num < queue.peek()) { 
  10.             queue.poll(); 
  11.             queue.add(num); 
  12.         } 
  13.     } 
  14.     int[] result = new int[k]; 
  15.     for (int i = 0; i < k; i++) { 
  16.         result[i] = queue.poll(); 
  17.     } 
  18.     return result; 
  19. } 

「快速排序」

把快速排序的過程簡單改一下就行了，我們根據基準值和k的的位置決定對左段還是右段進行排序即可，而不是對整個數組進行排序

  1. class Solution { 
  2.  
  3.     public int[] getLeastNumbers(int[] arr, int k) { 
  4.         if (arr.length == 0 || k == 0) { 
  5.             return new int[0]; 
  6.         } 
  7.         return quickSort(arr, 0, arr.length - 1, k - 1); 
  8.     } 
  9.  
  10.     public int[] quickSort(int[] nums, int left, int right, int k) { 
  11.         int index = sort(nums, left, right); 
  12.         if (index == k) { 
  13.             return Arrays.copyOf(nums, k + 1); 
  14.         } 
  15.         // 根據 index 和 k 的位置決定切左段還是右段 
  16.         return index > k ? quickSort(nums, left, index - 1, k) : quickSort(nums, index + 1, right, k); 
  17.     } 
  18.  
  19.     public int sort(int[] a, int left, int right) { 
  20.         int key = a[left]; 
  21.         while (left < right) { 
  22.             while (left < right && a[right] >= key) { 
  23.                 right--; 
  24.             } 
  25.             a[left] = a[right]; 
  26.             while (left < right && a[left] <= key) { 
  27.                 left++; 
  28.             } 
  29.             a[right] = a[left]; 
  30.         } 
  31.         a[left] = key; 
  32.         return left; 
  33.     } 
  34. } 

「計數排序」

因為題目中有這樣一個條件0 <= arr[i] <= 10000，說明數組中的元素比較集中，我們就可以用計數排序來解決這個問題，因為arr[i]的最大值10000為，所以我每次直接開一個10001大的數組

  1. public int[] getLeastNumbers(int[] arr, int k) { 
  2.     if (arr.length == 0 || k == 0) { 
  3.         return new int[0]; 
  4.     } 
  5.     int[] countArray = new int[10001]; 
  6.     for (int num : arr) { 
  7.         countArray[num]++; 
  8.     } 
  9.     int[] result = new int[k]; 
  10.     int index = 0; 
  11.     for (int i = 0; i < countArray.length && index < k; i++) { 
  12.         while (countArray[i] > 0 && index < k) { 
  13.             countArray[i]--; 
  14.             result[index++] = i; 
  15.         } 
  16.     } 
  17.     return result; 
  18. } 

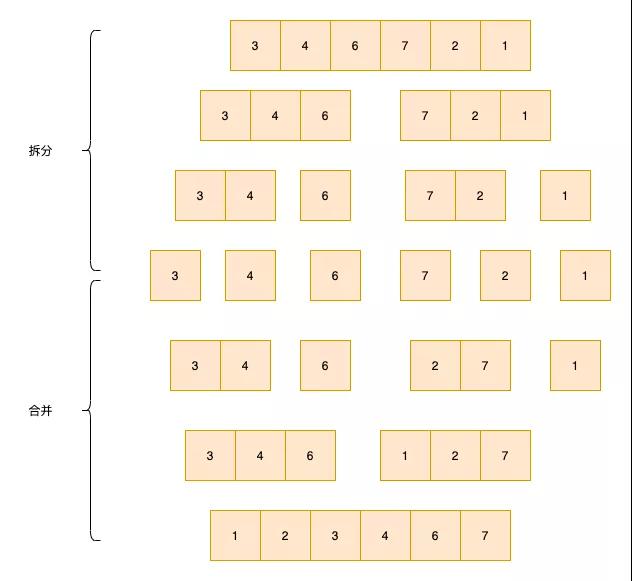
歸并排序

先把數組拆分為只有一個元素，然后對拆分的數組進行合并，主要合并的時候要保證合并后的數組有序，當合并完成時，整個數組有序

  1. public static void mergeSort(int[] a, int left, int right) { 
  2.     // 將數組分段成只有一個元素 
  3.     if (left == right) { 
  4.         return; 
  5.     } 
  6.     int mid = (left + right) / 2; 
  7.     mergeSort(a, left, mid); 
  8.     mergeSort(a, mid + 1, right); 
  9.     merge(a, left, mid, right); 
  10. } 
  11.  
  12. public static void merge(int[] a, int left, int mid, int right) { 
  13.     int[] temp = new int[right - left + 1]; 
  14.     int i = left; 
  15.     int j = mid + 1; 
  16.     int k = 0; 
  17.     while (i <= mid && j <= right) { 
  18.         if (a[i] < a[j]) { 
  19.             temp[k++] = a[i++]; 
  20.         } else { 
  21.             temp[k++] = a[j++]; 
  22.         } 
  23.     } 
  24.     // 復制左邊數組剩余的值 
  25.     while (i <= mid) { 
  26.         temp[k++] = a[i++]; 
  27.     } 
  28.     // 復制右邊數組剩余的值 
  29.     while (j <= right) { 
  30.         temp[k++] = a[j++]; 
  31.     } 
  32.     int index = 0; 
  33.     while (left <= right) { 
  34.         a[left++] = temp[index++]; 
  35.     } 
  36. } 

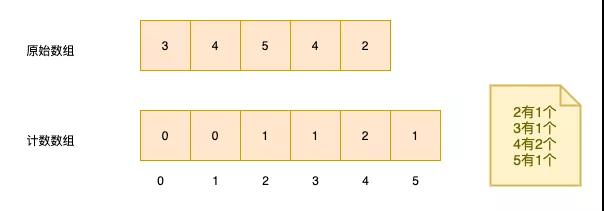
計數排序

新開辟一個數組，num[i]的含義為原數組中值為i的數有num[i]個。所以算法的局限性比較大，只適合數組元素跨度區間不大的場景。

  1. public static void countingSort(int[] a) { 
  2.     int max = Integer.MIN_VALUE; 
  3.     for (int num : a) { 
  4.         max = Integer.max(max, num); 
  5.     } 
  6.     int[] count = new int[max + 1]; 
  7.     for (int num : a) { 
  8.         count[num]++; 
  9.     } 
  10.     int index = 0; 
  11.     for (int i = 0; i < count.length; i++) { 
  12.         while (count[i] > 0) { 
  13.             a[index++] = i; 
  14.             count[i]--; 
  15.         } 
  16.     } 
  17. } 

上面的算法其實還有個缺陷，但數組中的元素為10000，10001，10002時，我們就得開辟一個10003大小的數組，不現實。所以我們可以改一下映射關系 num[i]的含義為原數組中值為i+min的個數為num[i]

進階版

  1. public static void countingSort(int[] a) { 
  2.     int max = Integer.MIN_VALUE; 
  3.     int min = Integer.MAX_VALUE; 
  4.     for (int num : a) { 
  5.         max = Integer.max(max, num); 
  6.         min = Integer.min(min, num); 
  7.     } 
  8.     int[] count = new int[max - min + 1]; 
  9.     for (int num : a) { 
  10.         count[num - min]++; 
  11.     } 
  12.     int index = 0; 
  13.     for (int i = 0; i < count.length; i++) { 
  14.         while (count[i] > 0) { 
  15.             a[index++] = i + min; 
  16.             count[i]--; 
  17.         } 
  18.     } 
  19. } 

「面試過程中經常會遇到求一個數組中的眾數時，就可以用計數排序的思想來解決」

基數排序

「面試過程中快拍和歸并排序問的比較多，應用場景也比較多」，基數排序基本沒被問到，不做解釋了。

桶排序

「前面我們提到的計數排序和基數排序可以說是桶排序思想的一種特殊體現，就是不需要進行數組元素之間的比較」。基本沒被問到，不做解釋了

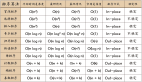
各種排序算法的應用

面試中常問的Top k問題，就可以先排序，然后求出Top k的元素。各種排序算法的效率如下圖片「更高效的思路是用堆和快排。Top K問題問法很多，本質思路都一樣，例如求前K個最大的元素，求前K個最小的元素，求前K個高頻元素」

本文轉載自微信公眾號「Java識堂」，可以通過以下二維碼關注。轉載本文請聯系Java識堂公眾號。

 

責任編輯：武曉燕 來源： Java識堂
排序算法面試
相關推薦

2021-10-31 07:38:37

排序算法代碼

2017-07-18 10:50:38

前端JavaScript排序算法

2022-03-10 12:03:33

Python算法代碼

2018-11-14 09:40:05

排序算法Java編程語言

2019-08-28 11:08:51

排序算法Java

2016-01-29 11:00:55

數據挖掘算法大數據

2013-02-25 09:46:35

數據挖掘算法ICDM

2018-02-01 18:45:12

機器學習算法線性回歸

2021-01-21 05:22:36

排序算法選擇

2021-01-26 05:33:07

排序算法快速

2010-08-31 14:01:48

CSS

2011-01-26 09:14:43

數據挖掘

2018-10-27 15:47:35

CART算法決策樹

2024-09-06 17:57:35

2013-07-09 13:56:48

微信

2018-09-13 12:51:58

數據挖掘算法樸素貝葉斯

2011-11-28 14:23:53

美信云網管

2015-11-11 08:36:40

數據中心網絡運維

2011-05-17 13:39:01

算法

2011-03-10 10:45:05

算法
點贊
收藏

51CTO技術棧公眾號

主站蜘蛛池模板： 成人午夜在线视频 | 九九热国产视频 | 欧美xxxx在线 | 国产视频不卡一区 | 91视频久久 | 国产视频福利一区 | 中文字幕国产精品视频 | 亚洲激情自拍偷拍 | 日韩在线精品 | 午夜视频一区 | 日本不卡一区二区三区在线观看 | 亚洲一区视频在线 | 国户精品久久久久久久久久久不卡 | 日韩视频一区在线观看 | 国产专区在线 | 免费看一区二区三区 | 精品九九九 | 亚洲视频欧美视频 | 精品久久香蕉国产线看观看亚洲 | 人人擦人人 | 91精品国产综合久久国产大片 | 东京av男人的天堂 | 成人免费在线视频 | 欧美一区二区三区在线观看 | 久久国产一区 | 亚洲人a | 九一视频在线播放 | 久久久久久高清 | 国产中文字幕亚洲 | 精品网站999 | 国产精品片 | 国产伦一区二区三区久久 | 一区二区三区不卡视频 | 日韩亚洲视频在线 | 亚洲一区二区电影在线观看 | 日韩电影一区二区三区 | 日韩在线不卡 | 最新国产视频 | 欧美黑人一区 | 成年视频在线观看 | 国产精品视频久久久久 |