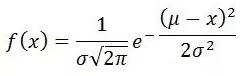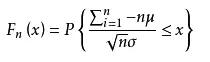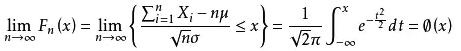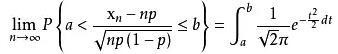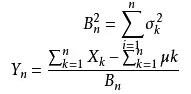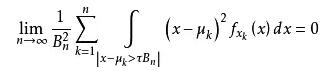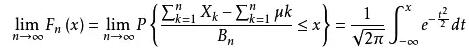大數據文摘出品

編譯：JonyKai、元元、云舟

高斯分布(Gaussian distribution)，也稱正態分布，最早由A.棣莫弗在求二項分布的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度導出了它。P.S.拉普拉斯和高斯研究了它的性質。是一個在數學、物理及工程等領域都非常重要的概率分布，在統計學的許多方面有著重大的影響力。

正態曲線呈鐘型，兩頭低，中間高，左右對稱因其曲線呈鐘形，因此人們又經常稱之為鐘形曲線。

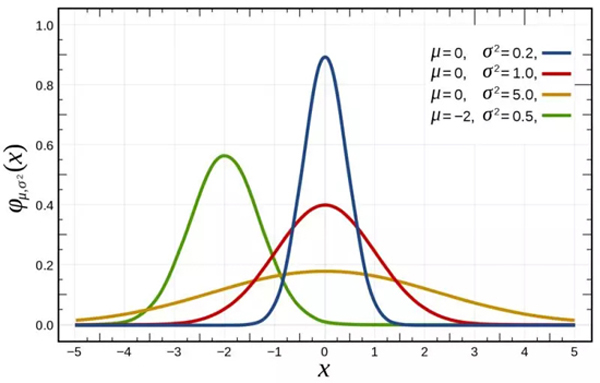
若隨機變量X服從一個數學期望為μ、方差為σ^2的正態分布，記為N(μ，σ^2)。其概率密度函數為正態分布的期望值μ決定了其位置，其標準差σ決定了分布的幅度。當μ = 0,σ = 1時的正態分布是標準正態分布。

高斯概率分布的數學表達式

一、在自然現象中隨處可見

[[233536]]

正在擴散的粒子的位置可以用正態分布來描述

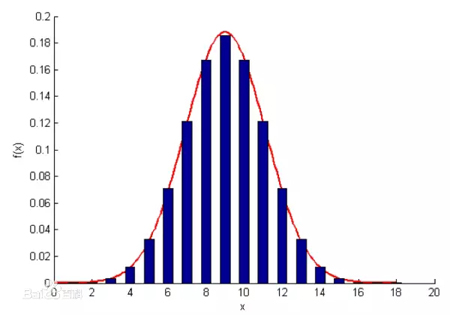
正態分布有極其廣泛的實際背景，生產與科學實驗中很多隨機變量的概率分布都可以近似地用正態分布來描述。例如，在生產條件不變的情況下，產品的強力、抗壓強度、口徑、長度等指標;同一種生物體的身長、體重等指標;同一種種子的重量;測量同一物體的誤差;彈著點沿某一方向的偏差;某個地區的年降水量;以及理想氣體分子的速度分量，等等。

一般來說，如果一個量是由許多微小的獨立隨機因素影響的結果，那么就可以認為這個量具有正態分布。從理論上看，正態分布具有很多良好的性質，許多概率分布可以用它來近似;還有一些常用的概率分布是由它直接導出的，例如對數正態分布、t分布、F分布等。

二、數學原因：中心極限定理

二維空間上進行200萬步的隨機游走之后得到的圖案

中心極限定理的內容為：大量獨立隨機變量的和經過適當標準化之后趨近于正態分布，與這些變量原本的分布無關。比如，隨機游走的總距離就趨近于正態分布。下面我們介紹三種形式的中心極限定理：

1. 獨立同分布的中心極限定理

設隨機變量X1，X2，......Xn，......獨立同分布，并且具有有限的數學期望和方差：E(Xi)=μ，D(Xi)=σ^2 (i=1,2....)，則對任意x，分布函數為

滿足

該定理說明，當n很大時，隨機變量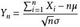近似地服從標準正態分布N(0，1)。因此，當n很大時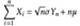，近似地服從正態分布N(nμ，nσ^2).該定理是中心極限定理最簡單又最常用的一種形式，在實際工作中，只要n足夠大，便可以把獨立同分布的隨機變量之和當作正態變量。這種方法在數理統計中用得很普遍，當處理大樣本時，它是重要工具。

2. 棣莫佛-拉普拉斯定理

設隨機變量X(n=1,2,...,)服從參數為n，p(0<p<1)的二項分布，則對于任意有限區間(a，b)有

該定理表明，正態分布是二項分布的極限分布，當數充分大時，我們可以利用上式來計算二項分布的概率。

3. 不同分布的中心極限定理

設隨機變量X1，X2，......Xn，......獨立同分布，它們的概率密度分別為fxk(x)，并有E(Xk)=μk，D(Xk)= σk^2，(k=1,2......)

若對任意正數τ，有：

對任意x，隨機變量Yn的分布函數Fn(x)，滿足：

該定理說明：所研究的隨機變量如果是有大量獨立的而且均勻的隨機變量相加而成，那么它的分布將近似于正態分布。

三、萬變不離其宗

與其他很多分布不同，正態分布進行適當的變換之后，仍是正態分布。

• 兩個正態分布之積仍是正態分布
• 兩個獨立的服從正態分布的隨機變量之和服從正態分布
• 對一個正態分布進行高斯卷積還是正態分布
• 正態分布經過傅立葉變換之后仍是正態分布

1. 簡潔

奧卡姆剃刀強調一個哲學原則：在其他條件都相同下，最簡單的解就是***的解。

對于任何一個用正態分布擬合的隨機分布，都可能存在一個多參數，更復雜，更準確的解法。但是我們仍然會傾向于選用正態分布，因為它在數學上很簡潔。

• 它的均值(mean)、中值(median)和眾數(mode)都相同
• 只需要用兩個參數就可以確定整個分布

2. 圖形特性：

• 集中性：正態曲線的高峰位于正中央，即均數所在的位置。
• 對稱性：正態曲線以均數為中心，左右對稱，曲線兩端永遠不與橫軸相交。
• 均勻變動性：正態曲線由均數所在處開始，分別向左右兩側逐漸均勻下降。
• 曲線與橫軸間的面積總等于1，相當于概率密度函數的函數從正無窮到負無窮積分的概率為1。即頻率的總和為100%。

相關報道：https://towardsdatascience.com/why-data-scientists-love-gaussian-6e7a7b726859

【本文是51CTO專欄機構大數據文摘的原創譯文，微信公眾號“大數據文摘（ id: BigDataDigest）”】

戳這里，看該作者更多好文