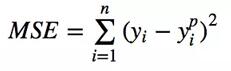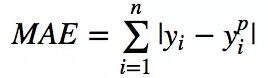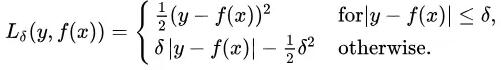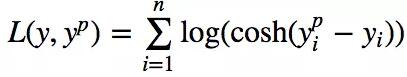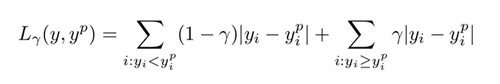機(jī)器學(xué)習(xí)大牛最常用的5個(gè)回歸損失函數(shù),你知道幾個(gè)?
大數(shù)據(jù)文摘出品
編譯:Apricock、睡不著的iris、JonyKai、錢天培
“損失函數(shù)”是機(jī)器學(xué)習(xí)優(yōu)化中至關(guān)重要的一部分。L1、L2損失函數(shù)相信大多數(shù)人都早已不陌生。那你了解Huber損失、Log-Cosh損失、以及常用于計(jì)算預(yù)測(cè)區(qū)間的分位數(shù)損失么?這些可都是機(jī)器學(xué)習(xí)大牛最常用的回歸損失函數(shù)哦!
機(jī)器學(xué)習(xí)中所有的算法都需要最大化或最小化一個(gè)函數(shù),這個(gè)函數(shù)被稱為“目標(biāo)函數(shù)”。其中,我們一般把最小化的一類函數(shù),稱為“損失函數(shù)”。它能根據(jù)預(yù)測(cè)結(jié)果,衡量出模型預(yù)測(cè)能力的好壞。
在實(shí)際應(yīng)用中,選取損失函數(shù)會(huì)受到諸多因素的制約,比如是否有異常值、機(jī)器學(xué)習(xí)算法的選擇、梯度下降的時(shí)間復(fù)雜度、求導(dǎo)的難易程度以及預(yù)測(cè)值的置信度等等。因此,不存在一種損失函數(shù)適用于處理所有類型的數(shù)據(jù)。這篇文章就講介紹不同種類的損失函數(shù)以及它們的作用。
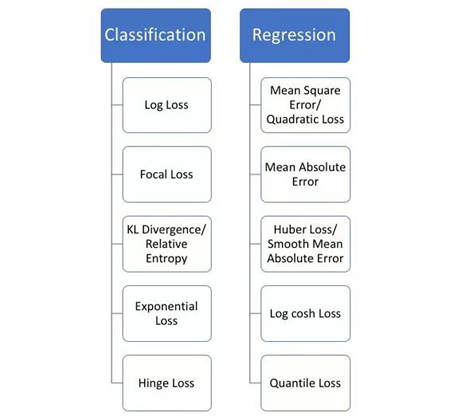
損失函數(shù)大致可分為兩類:分類問(wèn)題的損失函數(shù)和回歸問(wèn)題的損失函數(shù)。在這篇文章中,我將著重介紹回歸損失。
本文出現(xiàn)的代碼和圖表我們都妥妥保存在這兒了:
https://nbviewer.jupyter.org/github/groverpr/Machine-Learning/blob/master/notebooks/05_Loss_Functions.ipynb
分類、回歸問(wèn)題損失函數(shù)對(duì)比
均方誤差
均方誤差(MSE)是最常用的回歸損失函數(shù),計(jì)算方法是求預(yù)測(cè)值與真實(shí)值之間距離的平方和,公式如圖。
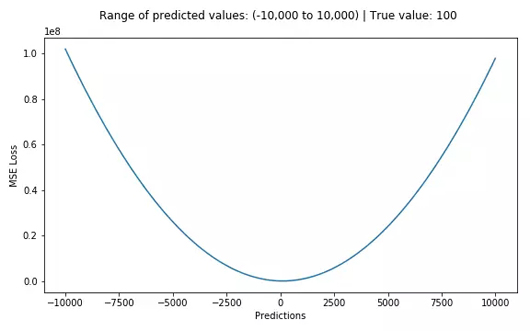
下圖是MSE函數(shù)的圖像,其中目標(biāo)值是100,預(yù)測(cè)值的范圍從-10000到10000,Y軸代表的MSE取值范圍是從0到正無(wú)窮,并且在預(yù)測(cè)值為100處達(dá)到最小。
MSE損失(Y軸)-預(yù)測(cè)值(X軸)
平均絕對(duì)值誤差(也稱L1損失)
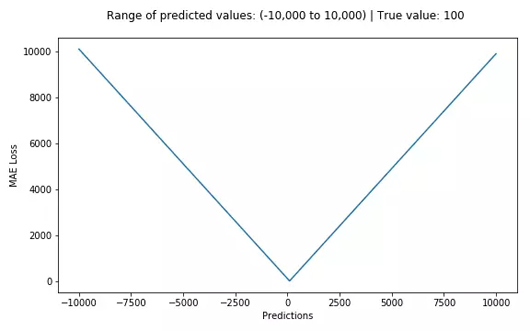
平均絕對(duì)誤差(MAE)是另一種用于回歸模型的損失函數(shù)。MAE是目標(biāo)值和預(yù)測(cè)值之差的絕對(duì)值之和。其只衡量了預(yù)測(cè)值誤差的平均模長(zhǎng),而不考慮方向,取值范圍也是從0到正無(wú)窮(如果考慮方向,則是殘差/誤差的總和——平均偏差(MBE))。
MAE損失(Y軸)-預(yù)測(cè)值(X軸)
1. MSE(L2損失)與MAE(L1損失)的比較
簡(jiǎn)單來(lái)說(shuō),MSE計(jì)算簡(jiǎn)便,但MAE對(duì)異常點(diǎn)有更好的魯棒性。下面就來(lái)介紹導(dǎo)致二者差異的原因。
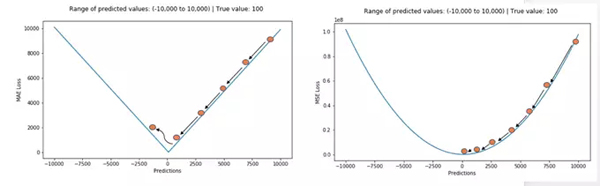
訓(xùn)練一個(gè)機(jī)器學(xué)習(xí)模型時(shí),我們的目標(biāo)就是找到損失函數(shù)達(dá)到極小值的點(diǎn)。當(dāng)預(yù)測(cè)值等于真實(shí)值時(shí),這兩種函數(shù)都能達(dá)到最小。
下面是這兩種損失函數(shù)的python代碼。你可以自己編寫(xiě)函數(shù),也可以使用sklearn內(nèi)置的函數(shù)。
- # true: Array of true target variable
- # pred: Array of predictions
- def mse(true, pred):
- return np.sum((true - pred)**2)
- def mae(true, pred):
- return np.sum(np.abs(true - pred))
- # also available in sklearn
- from sklearn.metrics import mean_squared_error
- from sklearn.metrics import mean_absolute_error
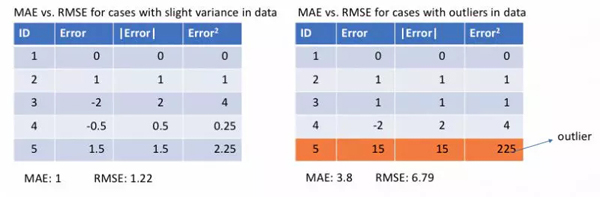
下面讓我們觀察MAE和RMSE(即MSE的平方根,同MAE在同一量級(jí)中)在兩個(gè)例子中的計(jì)算結(jié)果。第一個(gè)例子中,預(yù)測(cè)值和真實(shí)值很接近,而且誤差的方差也較小。第二個(gè)例子中,因?yàn)榇嬖谝粋€(gè)異常點(diǎn),而導(dǎo)致誤差非常大。
左圖:誤差比較接近 右圖:有一個(gè)誤差遠(yuǎn)大于其他誤差
2. 從圖中可以知道什么?應(yīng)當(dāng)如何選擇損失函數(shù)?
MSE對(duì)誤差取了平方(令e=真實(shí)值-預(yù)測(cè)值),因此若e>1,則MSE會(huì)進(jìn)一步增大誤差。如果數(shù)據(jù)中存在異常點(diǎn),那么e值就會(huì)很大,而e²則會(huì)遠(yuǎn)大于|e|。
因此,相對(duì)于使用MAE計(jì)算損失,使用MSE的模型會(huì)賦予異常點(diǎn)更大的權(quán)重。在第二個(gè)例子中,用RMSE計(jì)算損失的模型會(huì)以犧牲了其他樣本的誤差為代價(jià),朝著減小異常點(diǎn)誤差的方向更新。然而這就會(huì)降低模型的整體性能。
如果訓(xùn)練數(shù)據(jù)被異常點(diǎn)所污染,那么MAE損失就更好用(比如,在訓(xùn)練數(shù)據(jù)中存在大量錯(cuò)誤的反例和正例標(biāo)記,但是在測(cè)試集中沒(méi)有這個(gè)問(wèn)題)。
直觀上可以這樣理解:如果我們最小化MSE來(lái)對(duì)所有的樣本點(diǎn)只給出一個(gè)預(yù)測(cè)值,那么這個(gè)值一定是所有目標(biāo)值的平均值。但如果是最小化MAE,那么這個(gè)值,則會(huì)是所有樣本點(diǎn)目標(biāo)值的中位數(shù)。眾所周知,對(duì)異常值而言,中位數(shù)比均值更加魯棒,因此MAE對(duì)于異常值也比MSE更穩(wěn)定。
然而MAE存在一個(gè)嚴(yán)重的問(wèn)題(特別是對(duì)于神經(jīng)網(wǎng)絡(luò)):更新的梯度始終相同,也就是說(shuō),即使對(duì)于很小的損失值,梯度也很大。這樣不利于模型的學(xué)習(xí)。為了解決這個(gè)缺陷,我們可以使用變化的學(xué)習(xí)率,在損失接近最小值時(shí)降低學(xué)習(xí)率。
而MSE在這種情況下的表現(xiàn)就很好,即便使用固定的學(xué)習(xí)率也可以有效收斂。MSE損失的梯度隨損失增大而增大,而損失趨于0時(shí)則會(huì)減小。這使得在訓(xùn)練結(jié)束時(shí),使用MSE模型的結(jié)果會(huì)更精確。
根據(jù)不同情況選擇損失函數(shù)
如果異常點(diǎn)代表在商業(yè)中很重要的異常情況,并且需要被檢測(cè)出來(lái),則應(yīng)選用MSE損失函數(shù)。相反,如果只把異常值當(dāng)作受損數(shù)據(jù),則應(yīng)選用MAE損失函數(shù)。
推薦大家讀一下這篇文章,文中比較了分別使用L1、L2損失的回歸模型在有無(wú)異常值時(shí)的表現(xiàn)。
文章網(wǎng)址:http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
這里L(fēng)1損失和L2損失只是MAE和MSE的別稱。
總而言之,處理異常點(diǎn)時(shí),L1損失函數(shù)更穩(wěn)定,但它的導(dǎo)數(shù)不連續(xù),因此求解效率較低。L2損失函數(shù)對(duì)異常點(diǎn)更敏感,但通過(guò)令其導(dǎo)數(shù)為0,可以得到更穩(wěn)定的封閉解。
二者兼有的問(wèn)題是:在某些情況下,上述兩種損失函數(shù)都不能滿足需求。例如,若數(shù)據(jù)中90%的樣本對(duì)應(yīng)的目標(biāo)值為150,剩下10%在0到30之間。那么使用MAE作為損失函數(shù)的模型可能會(huì)忽視10%的異常點(diǎn),而對(duì)所有樣本的預(yù)測(cè)值都為150。
這是因?yàn)槟P蜁?huì)按中位數(shù)來(lái)預(yù)測(cè)。而使用MSE的模型則會(huì)給出很多介于0到30的預(yù)測(cè)值,因?yàn)槟P蜁?huì)向異常點(diǎn)偏移。上述兩種結(jié)果在許多商業(yè)場(chǎng)景中都是不可取的。
這些情況下應(yīng)該怎么辦呢?最簡(jiǎn)單的辦法是對(duì)目標(biāo)變量進(jìn)行變換。而另一種辦法則是換一個(gè)損失函數(shù),這就引出了下面要講的第三種損失函數(shù),即Huber損失函數(shù)。
Huber損失,平滑的平均絕對(duì)誤差
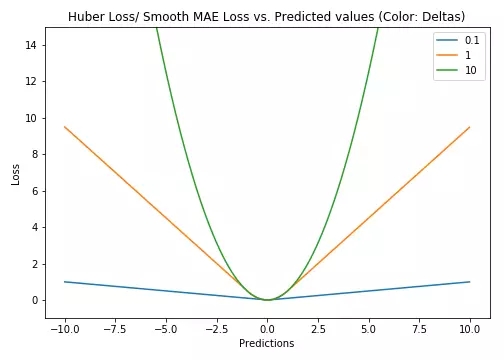
Huber損失對(duì)數(shù)據(jù)中的異常點(diǎn)沒(méi)有平方誤差損失那么敏感。它在0也可微分。本質(zhì)上,Huber損失是絕對(duì)誤差,只是在誤差很小時(shí),就變?yōu)槠椒秸`差。誤差降到多小時(shí)變?yōu)槎握`差由超參數(shù)δ(delta)來(lái)控制。當(dāng)Huber損失在[0-δ,0+δ]之間時(shí),等價(jià)為MSE,而在[-∞,δ]和[δ,+∞]時(shí)為MAE。
Huber損失(Y軸)與預(yù)測(cè)值(X軸)圖示。真值取0
這里超參數(shù)delta的選擇非常重要,因?yàn)檫@決定了你對(duì)與異常點(diǎn)的定義。當(dāng)殘差大于delta,應(yīng)當(dāng)采用L1(對(duì)較大的異常值不那么敏感)來(lái)最小化,而殘差小于超參數(shù),則用L2來(lái)最小化。
為何要使用Huber損失?
使用MAE訓(xùn)練神經(jīng)網(wǎng)絡(luò)最大的一個(gè)問(wèn)題就是不變的大梯度,這可能導(dǎo)致在使用梯度下降快要結(jié)束時(shí),錯(cuò)過(guò)了最小點(diǎn)。而對(duì)于MSE,梯度會(huì)隨著損失的減小而減小,使結(jié)果更加精確。
在這種情況下,Huber損失就非常有用。它會(huì)由于梯度的減小而落在最小值附近。比起MSE,它對(duì)異常點(diǎn)更加魯棒。因此,Huber損失結(jié)合了MSE和MAE的優(yōu)點(diǎn)。但是,Huber損失的問(wèn)題是我們可能需要不斷調(diào)整超參數(shù)delta。
Log-Cosh損失
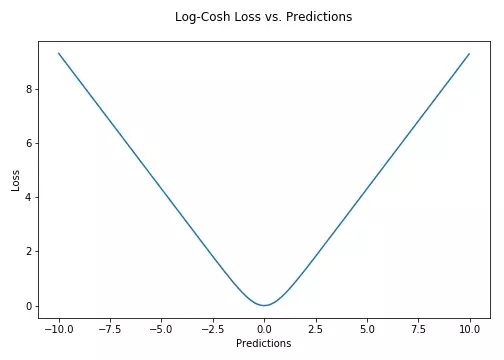
Log-cosh是另一種應(yīng)用于回歸問(wèn)題中的,且比L2更平滑的的損失函數(shù)。它的計(jì)算方式是預(yù)測(cè)誤差的雙曲余弦的對(duì)數(shù)。
Log-cosh損失(Y軸)與預(yù)測(cè)值(X軸)圖示。真值取0
優(yōu)點(diǎn):對(duì)于較小的x,log(cosh(x))近似等于(x^2)/2,對(duì)于較大的x,近似等于abs(x)-log(2)。這意味著‘logcosh’基本類似于均方誤差,但不易受到異常點(diǎn)的影響。它具有Huber損失所有的優(yōu)點(diǎn),但不同于Huber損失的是,Log-cosh二階處處可微。
為什么需要二階導(dǎo)數(shù)?許多機(jī)器學(xué)習(xí)模型如XGBoost,就是采用牛頓法來(lái)尋找最優(yōu)點(diǎn)。而牛頓法就需要求解二階導(dǎo)數(shù)(Hessian)。因此對(duì)于諸如XGBoost這類機(jī)器學(xué)習(xí)框架,損失函數(shù)的二階可微是很有必要的。
XgBoost中使用的目標(biāo)函數(shù)。注意對(duì)一階和二階導(dǎo)數(shù)的依賴性
但Log-cosh損失也并非完美,其仍存在某些問(wèn)題。比如誤差很大的話,一階梯度和Hessian會(huì)變成定值,這就導(dǎo)致XGBoost出現(xiàn)缺少分裂點(diǎn)的情況。
Huber和Log-cosh損失函數(shù)的Python代碼:
- # huber loss
- def huber(true, pred, delta):
- loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
- return np.sum(loss)
- # log cosh loss
- def logcosh(true, pred):
- loss = np.log(np.cosh(pred - true))
- return np.sum(loss)
分位數(shù)損失
在大多數(shù)現(xiàn)實(shí)世界預(yù)測(cè)問(wèn)題中,我們通常希望了解預(yù)測(cè)中的不確定性。清楚預(yù)測(cè)的范圍而非僅是估計(jì)點(diǎn),對(duì)許多商業(yè)問(wèn)題的決策很有幫助。
當(dāng)我們更關(guān)注區(qū)間預(yù)測(cè)而不僅是點(diǎn)預(yù)測(cè)時(shí),分位數(shù)損失函數(shù)就很有用。使用最小二乘回歸進(jìn)行區(qū)間預(yù)測(cè),基于的假設(shè)是殘差(y-y_hat)是獨(dú)立變量,且方差保持不變。
一旦違背了這條假設(shè),那么線性回歸模型就不成立。但是我們也不能因此就認(rèn)為使用非線性函數(shù)或基于樹(shù)的模型更好,而放棄將線性回歸模型作為基線方法。這時(shí),分位數(shù)損失和分位數(shù)回歸就派上用場(chǎng)了,因?yàn)榧幢銓?duì)于具有變化方差或非正態(tài)分布的殘差,基于分位數(shù)損失的回歸也能給出合理的預(yù)測(cè)區(qū)間。
下面讓我們看一個(gè)實(shí)際的例子,以便更好地理解基于分位數(shù)損失的回歸是如何對(duì)異方差數(shù)據(jù)起作用的。
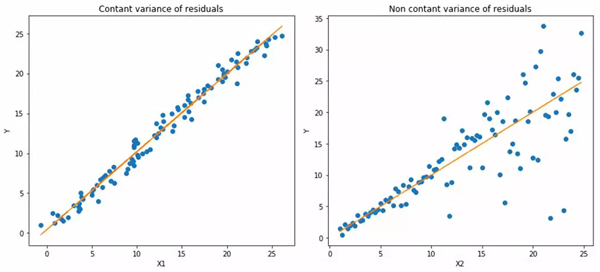
1. 分位數(shù)回歸與最小二乘回歸
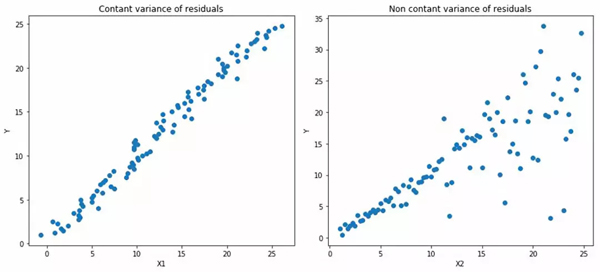
左:b/wX1和Y為線性關(guān)系。具有恒定的殘差方差。右:b/wX2和Y為線性關(guān)系,但Y的方差隨著X2增加。(異方差)
橙線表示兩種情況下OLS的估值
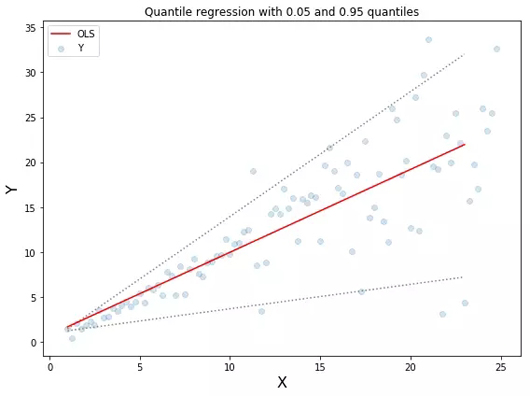
分位數(shù)回歸。虛線表示基于0.05和0.95分位數(shù)損失函數(shù)的回歸
附上圖中所示分位數(shù)回歸的代碼:
https://github.com/groverpr/Machine-Learning/blob/master/notebooks/09_Quantile_Regression.ipynb
2. 理解分位數(shù)損失函數(shù)
如何選取合適的分位值取決于我們對(duì)正誤差和反誤差的重視程度。損失函數(shù)通過(guò)分位值(γ)對(duì)高估和低估給予不同的懲罰。例如,當(dāng)分位數(shù)損失函數(shù)γ=0.25時(shí),對(duì)高估的懲罰更大,使得預(yù)測(cè)值略低于中值。
γ是所需的分位數(shù),其值介于0和1之間。
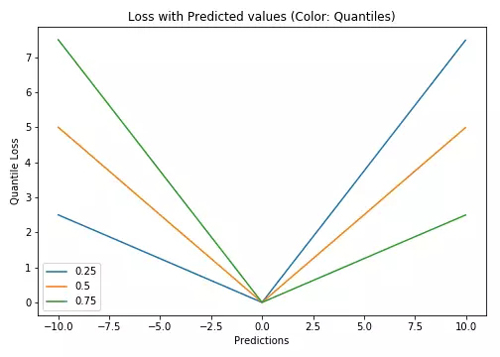
分位數(shù)損失(Y軸)與預(yù)測(cè)值(X軸)圖示。Y的真值為0
這個(gè)損失函數(shù)也可以在神經(jīng)網(wǎng)絡(luò)或基于樹(shù)的模型中計(jì)算預(yù)測(cè)區(qū)間。以下是用Sklearn實(shí)現(xiàn)梯度提升樹(shù)回歸模型的示例。
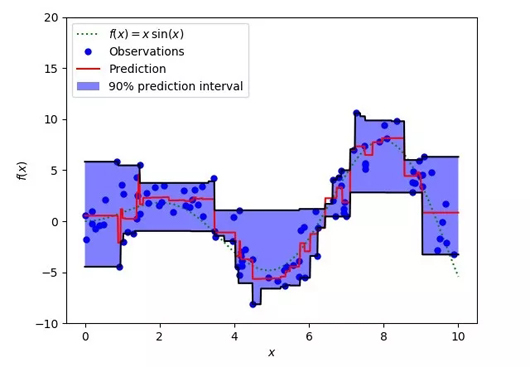
使用分位數(shù)損失(梯度提升回歸器)預(yù)測(cè)區(qū)間
上圖表明:在sklearn庫(kù)的梯度提升回歸中使用分位數(shù)損失可以得到90%的預(yù)測(cè)區(qū)間。其中上限為γ=0.95,下限為γ=0.05。
對(duì)比研究
為了證明上述所有損失函數(shù)的特點(diǎn),讓我們來(lái)一起看一個(gè)對(duì)比研究。首先,我們建立了一個(gè)從sinc(x)函數(shù)中采樣得到的數(shù)據(jù)集,并引入了兩項(xiàng)人為噪聲:高斯噪聲分量ε〜N(0,σ2)和脈沖噪聲分量ξ〜Bern(p)。
加入脈沖噪聲是為了說(shuō)明模型的魯棒效果。以下是使用不同損失函數(shù)擬合GBM回歸器的結(jié)果。
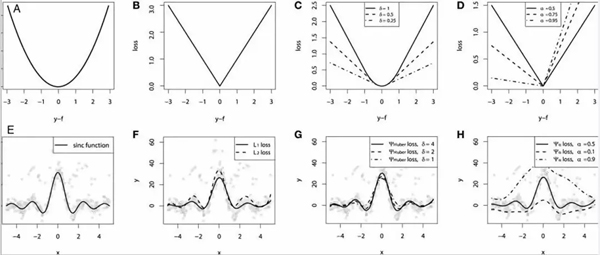
連續(xù)損失函數(shù):(A)MSE損失函數(shù);(B)MAE損失函數(shù);(C)Huber損失函數(shù);(D)分位數(shù)損失函數(shù)。將一個(gè)平滑的GBM擬合成有噪聲的sinc(x)數(shù)據(jù)的示例:(E)原始sinc(x)函數(shù);(F)具有MSE和MAE損失的平滑GBM;(G)具有Huber損失的平滑GBM,且δ={4,2,1};(H)具有分位數(shù)損失的平滑的GBM,且α={0.5,0.1,0.9}。
仿真對(duì)比的一些觀察結(jié)果:
- MAE損失模型的預(yù)測(cè)結(jié)果受脈沖噪聲的影響較小,而MSE損失函數(shù)的預(yù)測(cè)結(jié)果受此影響略有偏移。
- Huber損失模型預(yù)測(cè)結(jié)果對(duì)所選超參數(shù)不敏感。
- 分位數(shù)損失模型在合適的置信水平下能給出很好的估計(jì)。
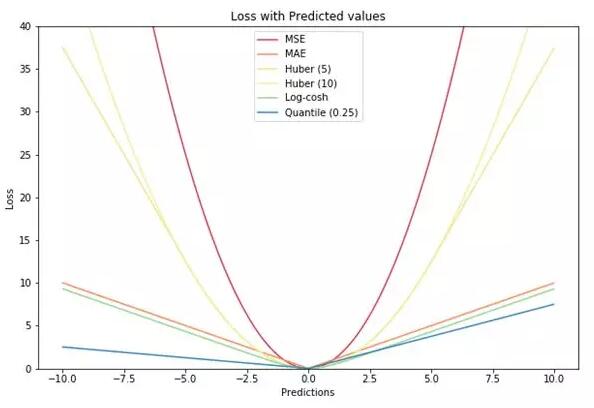
最后,讓我們將所有損失函數(shù)都放進(jìn)一張圖,我們就得到了下面這張漂亮的圖片!它們的區(qū)別是不是一目了然了呢。
相關(guān)報(bào)道:
https://heartbeat.fritz.ai/5-regression-loss-functions-all-machine-learners-should-know-4fb140e9d4b0
【本文是51CTO專欄機(jī)構(gòu)大數(shù)據(jù)文摘的原創(chuàng)譯文,微信公眾號(hào)“大數(shù)據(jù)文摘( id: BigDataDigest)”】