拜托,面試別再問我TopK了
面試中,TopK,是問得比較多的幾個問題之一,到底有幾種方法,這些方案里蘊含的優化思路究竟是怎么樣的,今天和大家聊一聊。
畫外音:除非校招,我在面試過程中從不問TopK這個問題,默認大家都知道。
問題描述:從arr[1, n]這n個數中,找出***的k個數,這就是經典的TopK問題。
栗子:從arr[1, 12]={5,3,7,1,8,2,9,4,7,2,6,6} 這n=12個數中,找出***的k=5個。
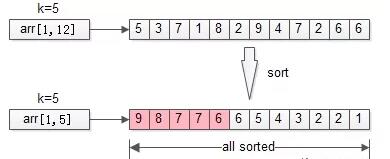
一、排序
排序是最容易想到的方法,將n個數排序之后,取出***的k個,即為所得。
偽代碼:
- sort(arr, 1, n);
- return arr[1, k];
時間復雜度:O(n*lg(n))
分析:明明只需要TopK,卻將全局都排序了,這也是這個方法復雜度非常高的原因。那能不能不全局排序,而只局部排序呢?這就引出了第二個優化方法。
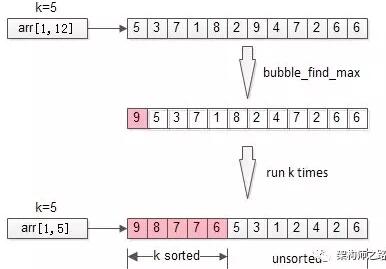
二、局部排序
不再全局排序,只對***的k個排序。
冒泡是一個很常見的排序方法,每冒一個泡,找出***值,冒k個泡,就得到TopK。
偽代碼:
- for(i=1 to k){
- bubble_find_max(arr,i);
- }
- return arr[1, k];
時間復雜度:O(n*k)
分析:冒泡,將全局排序優化為了局部排序,非TopK的元素是不需要排序的,節省了計算資源。不少朋友會想到,需求是TopK,是不是這***的k個元素也不需要排序呢?這就引出了第三個優化方法。
三、堆
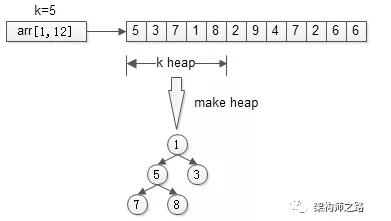
思路:只找到TopK,不排序TopK。
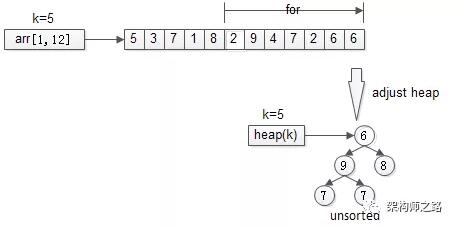
先用前k個元素生成一個小頂堆,這個小頂堆用于存儲,當前***的k個元素。
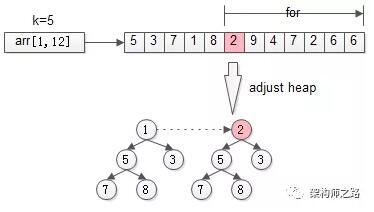
接著,從第k+1個元素開始掃描,和堆頂(堆中最小的元素)比較,如果被掃描的元素大于堆頂,則替換堆頂的元素,并調整堆,以保證堆內的k個元素,總是當前***的k個元素。
直到,掃描完所有n-k個元素,最終堆中的k個元素,就是猥瑣求的TopK。
偽代碼:
- heap[k] = make_heap(arr[1, k]);
- for(i=k+1 to n){
- adjust_heap(heep[k],arr[i]);
- }
- return heap[k];
時間復雜度:O(n*lg(k))
畫外音:n個元素掃一遍,假設運氣很差,每次都入堆調整,調整時間復雜度為堆的高度,即lg(k),故整體時間復雜度是n*lg(k)。
分析:堆,將冒泡的TopK排序優化為了TopK不排序,節省了計算資源。堆,是求TopK的經典算法,那還有沒有更快的方案呢?
四、隨機選擇
隨機選擇算在是《算法導論》中一個經典的算法,其時間復雜度為O(n),是一個線性復雜度的方法。
這個方法并不是所有同學都知道,為了將算法講透,先聊一些前序知識,一個所有程序員都應該爛熟于胸的經典算法:快速排序。
畫外音:
- 如果有朋友說,“不知道快速排序,也不妨礙我寫業務代碼呀”…額...
- 除非校招,我在面試過程中從不問快速排序,默認所有工程師都知道;
其偽代碼是:
- void quick_sort(int[]arr, int low, inthigh){
- if(low== high) return;
- int i = partition(arr, low, high);
- quick_sort(arr, low, i-1);
- quick_sort(arr, i+1, high);
- }
其核心算法思想是,分治法。
分治法(Divide&Conquer),把一個大的問題,轉化為若干個子問題(Divide),每個子問題“都”解決,大的問題便隨之解決(Conquer)。這里的關鍵詞是“都”。從偽代碼里可以看到,快速排序遞歸時,先通過partition把數組分隔為兩個部分,兩個部分“都”要再次遞歸。
分治法有一個特例,叫減治法。
減治法(Reduce&Conquer),把一個大的問題,轉化為若干個子問題(Reduce),這些子問題中“只”解決一個,大的問題便隨之解決(Conquer)。這里的關鍵詞是“只”。
二分查找binary_search,BS,是一個典型的運用減治法思想的算法,其偽代碼是:
- int BS(int[]arr, int low, inthigh, int target){
- if(low> high) return -1;
- mid= (low+high)/2;
- if(arr[mid]== target) return mid;
- if(arr[mid]> target)
- return BS(arr, low, mid-1, target);
- else
- return BS(arr, mid+1, high, target);
- }
從偽代碼可以看到,二分查找,一個大的問題,可以用一個mid元素,分成左半區,右半區兩個子問題。而左右兩個子問題,只需要解決其中一個,遞歸一次,就能夠解決二分查找全局的問題。
通過分治法與減治法的描述,可以發現,分治法的復雜度一般來說是大于減治法的:
- 快速排序:O(n*lg(n))
- 二分查找:O(lg(n))
話題收回來,快速排序的核心是:
- i = partition(arr, low, high);
1. 這個partition是干嘛的呢?
顧名思義,partition會把整體分為兩個部分。
更具體的,會用數組arr中的一個元素(默認是***個元素t=arr[low])為劃分依據,將數據arr[low, high]劃分成左右兩個子數組:
- 左半部分,都比t大
- 右半部分,都比t小
- 中間位置i是劃分元素
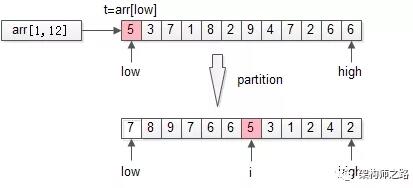
以上述TopK的數組為例,先用***個元素t=arr[low]為劃分依據,掃描一遍數組,把數組分成了兩個半區:
- 左半區比t大
- 右半區比t小
- 中間是t
partition返回的是t最終的位置i。
很容易知道,partition的時間復雜度是O(n)。
畫外音:把整個數組掃一遍,比t大的放左邊,比t小的放右邊,***t放在中間N[i]。
2. partition和TopK問題有什么關系呢?
TopK是希望求出arr[1,n]中***的k個數,那如果找到了第k大的數,做一次partition,不就一次性找到***的k個數了么?
畫外音:即partition后左半區的k個數。
問題變成了arr[1, n]中找到第k大的數。
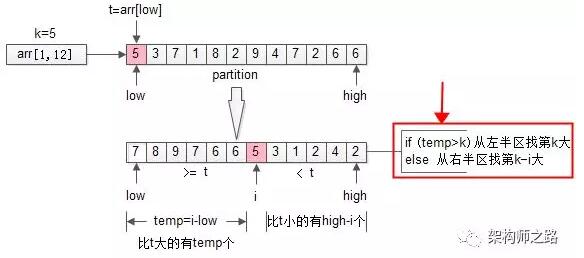
再回過頭來看看***次partition,劃分之后:
- i = partition(arr, 1, n);
- 如果i大于k,則說明arr[i]左邊的元素都大于k,于是只遞歸arr[1, i-1]里第k大的元素即可;
- 如果i小于k,則說明說明第k大的元素在arr[i]的右邊,于是只遞歸arr[i+1, n]里第k-i大的元素即可;
畫外音:這一段非常重要,多讀幾遍。
這就是隨機選擇算法randomized_select,RS,其偽代碼如下:
- int RS(arr, low, high, k){
- if(low== high) return arr[low];
- i= partition(arr, low, high);
- temp= i-low; //數組前半部分元素個數
- if(temp>=k)
- return RS(arr, low, i-1, k); //求前半部分第k大
- else
- return RS(arr, i+1, high, k-i); //求后半部分第k-i大
- }
這是一個典型的減治算法,遞歸內的兩個分支,最終只會執行一個,它的時間復雜度是O(n)。
再次強調一下:
- 分治法,大問題分解為小問題,小問題都要遞歸各個分支,例如:快速排序
- 減治法,大問題分解為小問題,小問題只要遞歸一個分支,例如:二分查找,隨機選擇
通過隨機選擇(randomized_select),找到arr[1, n]中第k大的數,再進行一次partition,就能得到TopK的結果。
五、總結
TopK,不難;其思路優化過程,不簡單:
- 全局排序,O(n*lg(n))
- 局部排序,只排序TopK個數,O(n*k)
- 堆,TopK個數也不排序了,O(n*lg(k))
- 分治法,每個分支“都要”遞歸,例如:快速排序,O(n*lg(n))
- 減治法,“只要”遞歸一個分支,例如:二分查找O(lg(n)),隨機選擇O(n)
- TopK的另一個解法:隨機選擇+partition
【本文為51CTO專欄作者“58沈劍”原創稿件,轉載請聯系原作者】