[[323204]]

前言

在求三角形最短路徑和時，能否用貪心算法求解。所以本文打算對貪心算法進行簡單地介紹，介紹完之后我們再來看看是否這道三角形最短路徑問題能用貪心算法來求解。

本文將會從以下幾個方面來介紹貪心算法

• 什么是貪心算法
• 貪心算法例題詳題
• 貪心算法適用場景
• 再看三角形最短路徑和是否能用貪心算法求解

什么是貪心算法

貪心算法是指在每個階段做選擇的時候都做出當前階段(或狀態)最好的選擇，并且期望這樣做到的結果是全局最優解(但未必是全局最優解)

貪心算法其實是動態規劃的一種,由于它的「貪心」，只著眼于當前階段的最優解，所以每個子問題只會被計算一次，如果由此能得出全局最優解，相對于動態規劃要對每個子問題求全局最優解，它的時間復雜度無疑是會下降一個量級的。

舉個簡單的例子，比如給定某個數字的金額(如 250)與 100, 50, 10, 5, 1 這些紙幣(不限量)，怎么能用最少張的紙幣來兌換這張金額呢，顯然每次兌換應該先從大額的紙幣兌換起，第一次選 100， 第二次還是選 100， 第三次選第二大的 50 元，每次都選小于剩余金額中的最大面額的紙幣，這樣得出的解一定是全局最優解!時間復雜度無疑是線性的。

我們先來看幾道可以用貪心算法來求解的例題

貪心算法例題詳題

分糖果

• 有 m 個糖果和 n 個孩子。我們現在要把糖果分給這些孩子吃，但是糖果少，孩子多(m < n)，所以糖果只能分配給一部分孩子。每個糖果的大小不等，這 m 個糖果的大小分別是s1，s2，s3，……，sm。除此之外，每個孩子對糖果大小的需求也是不一樣的，只有糖果的大小大于等于孩子的對糖果大小的需求的時候，孩子才得到滿足。假設這 n 個孩子對糖果大小的需求分別是 g1，g2，g3，……，gn。那么如何分配糖果，能盡可能滿足最多數量的孩子呢?

求解：這道題如果用貪心來解解題思路還是比較明顯的，對于每個小孩的需求 gn，只要給他所有大小大于 gn 的糖果中的最小值即可，這樣就能把更大的糖果讓給需求更大的小孩。整個代碼如下：

public class Solution { 
    /** 
     *  獲取能分配給小孩且符合條件的最多糖果數 
     */ 
    private static int dispatchCandy(int[] gList, int[] sList) { 
        Arrays.sort(gList);     // 小孩對糖果的需求從小到大排列 
        Arrays.sort(sList);     // 糖果大小從小到大排列 
 
        int maximumCandyNum = 0; 
        for (int i = 0; i < gList.length; i++) { 
            for (int j = 0; j < sList.length; j++) { 
                // 選擇最接近小孩需求的糖果，以便讓更大的糖果滿足需求更大的小孩 
                if (gList[i] <= sList[j]) { 
                    maximumCandyNum++; 
                    // 糖果被選中，將其置為-1，代表無效了 
                    sList[j] = -1; 
                    // 當前小孩糖果已選中，跳出 
                    break; 
                } 
            } 
        } 
        return maximumCandyNum; 
    } 
 
    public static  void main(String[] args) { 
        // 小孩對糖果的需求 
        int[] gList = {1,2,4,6}; 
        // 糖果實際大小 
        int[] sList = {1,2,7,3}; 
        int result = dispatchCandy(gList, sList); 
        System.out.println("result = " + result); 
    } 
} 

無重疊區間

• 給定一個區間的集合，找到需要移除區間的最小數量，使剩余區間互不重疊。注意:可以認為區間的終點總是大于它的起點。區間 [1,2] 和 [2,3] 的邊界相互“接觸”，但沒有相互重疊。
• 示例 1: 輸入: [ [1,2], [2,3], [3,4], [1,3] ] 輸出: 1 解釋: 移除 [1,3] 后，剩下的區間沒有重疊。
• 示例 2: 輸入: [ [1,2], [1,2], [1,2] ] 輸出: 2 解釋: 你需要移除兩個 [1,2] 來使剩下的區間沒有重疊。
• 示例 3: 輸入: [ [1,2], [2,3] ] 輸出: 0 解釋: 你不需要移除任何區間，因為它們已經是無重疊的了。

區間重疊可以在生活中的很多場景里找到，比如任務調度，一個工人在一段時間內需要完成多項任務，每個任務需要完成的時間不同，如何在這段時間內讓工人盡可能多地完成這些任務呢(任務與任務之間進行的時間不能重疊，一個工人不可能在同一段時間內同時進行兩項任務)

解題思路: 這道題我們分別用動態規劃和貪心算法來解一下，以便對比一下兩者的時間復雜度，看下貪心算法是否在時間復雜度上更優勝一些。

動態規劃解法

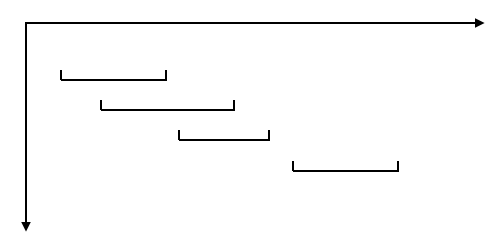
首先為了方便求解，我們把每個區間按區間的起始點從小到大進行排序，如圖示

 

接下來我們套用上篇中的說的動態規劃解題四步曲來看看怎么用動態規劃進行求解。

1、 判斷是否可用遞歸來解

其實直觀地看上面我們排好序的各個區間，這不就是個組合嗎，每個區間要么選，要么不選，把所有的組合窮舉出來，再看哪個組合最符合題目中的條件，所以無疑是可以用遞歸的(組合用遞歸怎么解，強烈建議看下這篇文章)。

不過這題的組合有點特殊，前后兩個區間有條件限制，如果當前區間與前一個區間重疊，則這兩者只能取其一(另一個需要剔除掉防止重疊)，于是我們有如下思路：

定義兩個值, pre , cur ，分別代表前一個區間與當前區間，需要進行如下步驟

• 比較前一個區間的終點與當前區間的起始值
• 如果前一個區間的終點小于當前區間的起始值，代表兩區間不重疊，則將 pre 置為 cur, cur 置為 cur + 1, 開始接下來緊鄰的兩個區間的判斷(即重復步驟 1)。
• 如果前一個區間的終點大于當前區間的起始值，代表兩區間重疊，則 pre 不變, cur 置為 cur + 1 (即將 cur 對應的區間移除)，注意此時移除區間數要加 1, 然后開始接下來 pre，cur+1 區間的判斷(即重復步驟 1)。

注：首次區間遍歷我們定義 pre = -1，cur = 0

從以上的描述中可以很明顯地看到存在遞歸現象，于是我們寫出了如下代碼,關鍵代碼都作了詳細的注釋。

public class Solution { 
    // 區間類，包括起始值和終止值 
    private  static  class Interval { 
        int start; 
        int end; 
        Interval(int start, int end) { 
            this.start = start; 
            this.end = end; 
        } 
    } 
 
    private static Integer removeDuplicateIntervas(Interval[] intervals) { 
        // 將區間按起始點由小到大進行排序 
        Arrays.sort(intervals, Comparator.comparingInt(a -> a.start)); 
        // 首次遍歷從 -1,0 開始 
        return removeSubDuplicate(-1, 0, intervals); 
    } 
 
    private static Integer removeSubDuplicate(int pre, int cur, Interval[] intervals) { 
        if (cur == intervals.length) { 
            return  0; 
        } 
 
        int notRemove = Integer.MAX_VALUE; 
        if (pre == -1 || intervals[pre].end <= intervals[cur].start) { 
 
            /** 
             * 如果是首次遍歷，或者 pre 區間的終點小于 cur 區間的起點（即區間不重疊）, 
             * 則 pre = cur; cur = cur+1 
             */ 
            notRemove = removeSubDuplicate(cur, cur+1, intervals); 
        } 
 
        /** 
         * 如果 pre 區間的終點大于 cur 區間的起點，代表兩區間重疊，cur 指向后一個區間，即 cur = cur + 1 
         * 代表 cur 被移除，所以需要加1（代表這個區間被移除了） 
         */ 
        int remove = removeSubDuplicate(pre, cur+1, intervals) + 1; 
 
        // 取兩者的較小值 
        return Math.min(notRemove, remove); 
    } 
 
    public static  void main(String[] args) { 
        // 初始化區間 
        Interval[] intervals = { 
                new Interval(1, 2), 
                new Interval(3, 5), 
                new Interval(4, 7), 
                new Interval(8, 10), 
                new Interval(9, 11) 
        }; 
        int result = removeDuplicateIntervas(intervals); 
        System.out.println("result = " + result); 
    } 
} 

2、 分析在遞歸的過程中是否存在大量的重復子問題

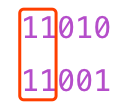
怎么判斷是否存在大量的重復子問題，在一文學會動態規劃解題技巧 我們提出一種方案，畫出遞歸樹 ，不過這題如果畫出遞歸樹比較麻煩，其實對于組合問題我們可以簡單分析一下，對于每個區間要么選，要么不選，我們以 1 代表該區間被選擇，以 0 代表該區間不選，則簡單考慮一下如下兩個組合

11010 
11001 

仔細看，紅框 部分，就是重復子問題!

 

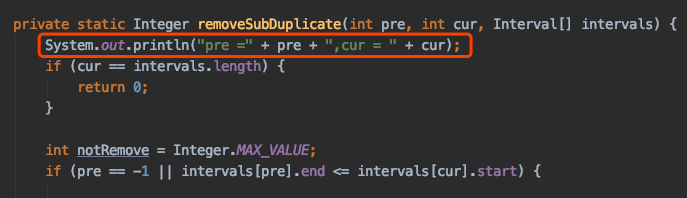
可能有人會說這樣分析也有點難，那我再教大家一招，打印! 如圖示

 

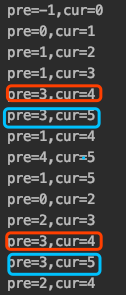
在遞歸函數中打印出來，然后分析打印的規律

 

可以看到，確實存在著重復子問題，時間復雜度是多少呢，每個區間要么選，要么不選，共有兩個狀態，如果有 n 個區間的話，就是 2^n,于是我們知道時間復雜度是 O(2^n)，指數級!顯然無法接受

既然存在重復子問題，那我們進入動態規劃第三步

3、采用備忘錄的方式來存子問題的解以避免大量的重復計算(剪枝)

在以上的分析中基本我們看到，其實就是 pre, cur 有可能存在大量重復，于是我們保存 pre, cur 對應的中間結果，如下

// 保存中間結果 
private static HashMap<String, Integer> map = new HashMap(); 
private static Integer removeSubDuplicate(int pre, int cur, Interval[] intervals) { 
    String key = pre + "," + cur; 
    if (map.get(key) != null) { 
        return map.get(key); 
    } 
     
    if (cur == intervals.length) { 
        return 0; 
    } 
 
    int notRemove = Integer.MAX_VALUE; 
    if (pre == -1 || intervals[pre].end <= intervals[cur].start) { 
        notRemove = removeSubDuplicate(cur, cur+1, intervals); 
    } 
 
    int remove = removeSubDuplicate(pre, cur+1, intervals) + 1; 
    int result = Math.min(notRemove, remove); 
    map.put(key, result); 
    return result; 
} 

采用備忘錄的方式緩存子問題的中間結果后，時間復雜度直線下降，達到 O(n^2)(因為 pre, cur 兩個變量不斷往后移，即兩層循環，所以是 O(n^2)) 。

4、改用自底向上的方式來遞推，即動態規劃

我們定義 dp[i] 為 從 0 到 第 i 個區間的最大不重疊區間數,于是我們得出了狀態轉移方程

dp[i] = max{dp[j]} + 1, 其中 0 <=j < i 并且需要滿足一個條件 interval[i].start > interval[j].end,即保證 i, j 指向的區間不重疊。 

則最終的 dp[區間總個數-1] 即為最大的連續不重疊區間個數，那么區間總個數 - 最大的連續不重疊區間個數不就是最小要移除的區間數了，有了 dp 方程，寫起代碼來就快了，如下

/** 
* 判斷兩區間是否重疊, i 區間的起點比 j 區間的大, 如果 j 區間的終點比 i 區間的起點大，則重疊 
 */ 
private static boolean isOverlapping(Interval i, Interval j) { 
    return j.end > i.start; 
} 
 
/** 
 * 動態規劃求解 
 */ 
private static Integer removeSubDuplicateWithDP(Interval[] intervals) { 
    // 將區間按起始點由小到大進行排序 
    Arrays.sort(intervals, Comparator.comparingInt(a -> a.start)); 
 
    int[] dp = new int[intervals.length]; 
    Arrays.fill(dp, 0); 
    dp[0]  = 1;    // 將 dp[0] 置為 1， 因為就算所有的區間都重疊，則連續不重疊區間到少也為 1 
 
    int result = 1; 
    for (int i = 1; i < intervals.length; i ++) { 
        int max = 0; 
        for (int j = 0; j < i; j ++) { 
            if (!isOverlapping(intervals[i], intervals[j])) { 
                max = Math.max(dp[j], max); 
            } 
        } 
        dp[i] = max + 1; 
    } 
    return intervals.length - dp[intervals.length - 1]; 
} 

空間復雜度是多少，由于只有一個 dp 一維數組，所以是 O(n)，時間復雜度呢， 兩重循環，所以是 O(n^2)。可以看到和采用遞歸+備忘錄的時間復雜度一樣，不過之前其實說了很多次，遞歸容易導致棧溢出，所以建議還是采用動態規劃的方式來求解。

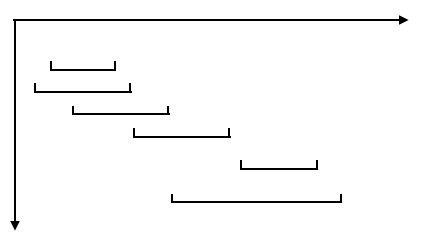
接下來重點來了，來看看如何用貪心算法來求解。首先要把各個區間按照區間的終點從小到大排列，如下

 

我們的思路與上文中的動態規劃一樣，先求出最大不重疊子區間個數,再用「區間總數-最大不重疊子區間個數」即為最小要移除的重疊區間數。

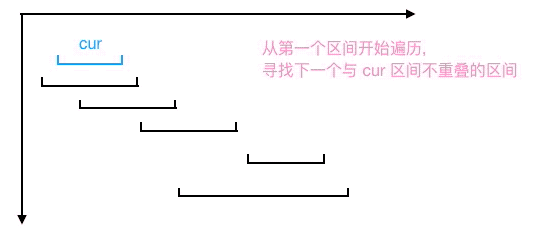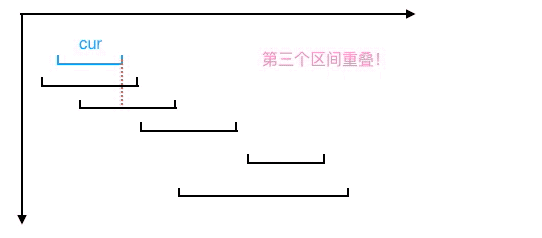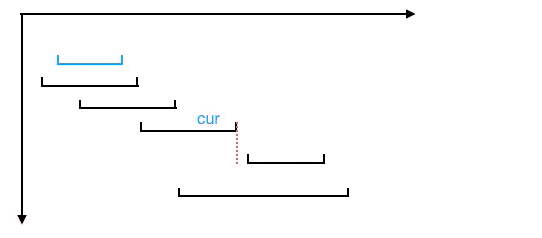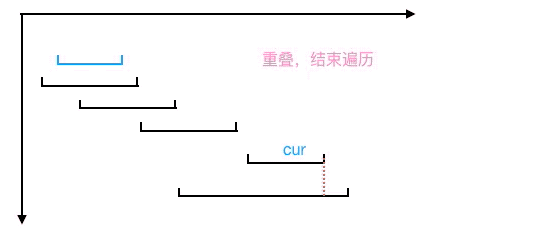
用貪心算法求最大不重大子區間個數步驟如下

1. 選擇終點最小的區間，設置為當前區間 cur 。
2. 按區間終點從小到大尋找下一個與區間 cur 不重疊的區間，然后將此區間設置為當前區間 cur(注意此時最大不重疊子區間個數要加1)，不斷重復步驟 2， 直到遍歷所有的區間。

動圖如下,相信大家看完動圖會更容易理解

 

知道了解題思路，寫代碼就很簡單了

/** 
 * 貪心算法求解 
 */ 
private static Integer removeSubDuplicateWithGreedy(Interval[] intervals) { 
    // 將區間終點由小到大進行排序 
    Arrays.sort(intervals, Comparator.comparingInt(a -> a.end)); 
 
    int cur = 0;            // 設置第一個為當前區間 
    int count = 1;      // 最大不重疊區間數,最小為1 
    for (int i = 1; i < intervals.length; i++) { 
        // 不重疊 
        if (intervals[cur].end < intervals[i].start) { 
            cur = i; 
            count++; 
        } 
    } 
    // 總區間個數減去最大不重疊區間數即最小被移除重疊區間 
    return intervals.length - count; 
} 

時間復雜度是多少呢，只有一個循環，所以是 O(n), 比起動態規劃的 O(n^2),確實快了一個數量級，簡單分析下為啥貪心算法這么快，由以上代碼可以看到，它只關心眼前的最優解(選擇下一個與當前區間不重疊的區間再依次遍歷，選完之后再也無需關心之前的區間了!)而動態規劃呢，從它的 dp 方程(dp[i] = max{dp[j]} + 1)可以看出，對于每個 i ,都要自底向上遍歷一遍 0 到 i 的解以求出最大值，也就是說對于動態規劃的子問題而言，由于它追求的是全局最優解，所以它有一個回溯(即自底向上求出所有子問題解的最優解)的過程，回溯的過程中就有一些重復的子問題計算，而貪心算法由于追求的是眼前的最優解，所以不會有這種回溯的求解，也就省去了大量的操作，所以如果可以用貪心算法求解，時間復雜度無疑是能上升一個量級的。

貪心算法適用場景

簡單總結一下貪心算法，它指的是每一步只選最優的，并且期望每一步選擇的最優解能達成全局的最優解，說實話這太難了，因為一般一個問題的選擇都會影響下一個問題的選擇，除非子問題之間完全獨立，沒有關聯，比如我們在文中開頭說的湊零錢的例子， 如果一個國家的鈔票比較奇葩，只有 1，5，11 這三種面值的鈔票，如何用最少的鈔票湊出 15 呢，如果用貪心第一次選 11， 那之后只能選 4 張 1 了，即 15 = 1 x 11 + 4 x1。其實最優解應該是 3 張 5 元的鈔票，為啥這種情況下用貪心不適用呢，因為第一次選了 11，影響了后面鈔票的選擇，也就是說子問題之間并不是獨立的，而是互相制約，互有影響的，所以我們選貪心的時候一定要注意它的適用場景。

再看三角形最短路徑和是否能用貪心算法求解

回過頭來看開頭的問題，三角形最短路徑和能否用貪心算法求解呢

先回顧一下這個題目:

 

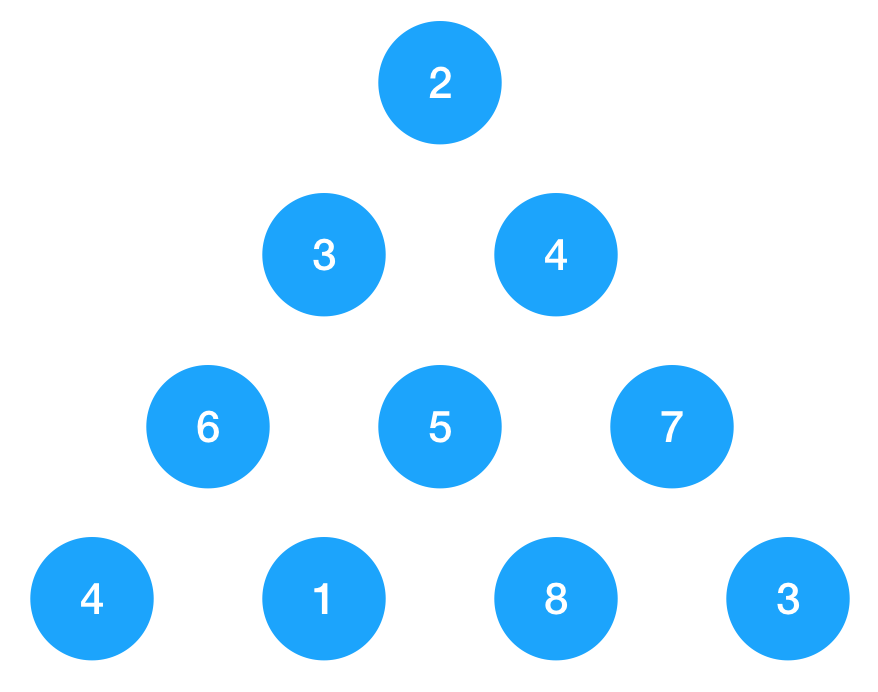
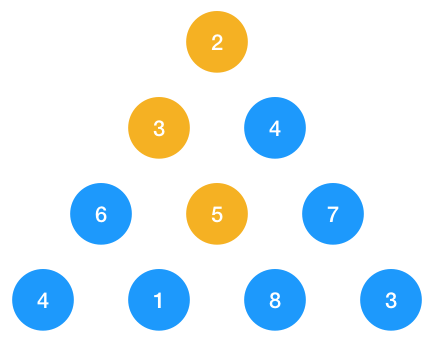
如圖示，以上三角形由一連串的數字構成，要求從頂點 2 開始走到最底下邊的最短路徑，每次只能向當前節點下面的兩個節點走，如 3 可以向 6 或 5 走，不能直接走到 7。

如圖示：要求節點 2 到底部的最短路徑，它只關心節點 9， 10，之前層數的節點無需再關心!因為 9，10 已經是最優子結構了，所以只保存每層節點(即一維數組)的最值即可!

 

如果用貪心算法怎么求解

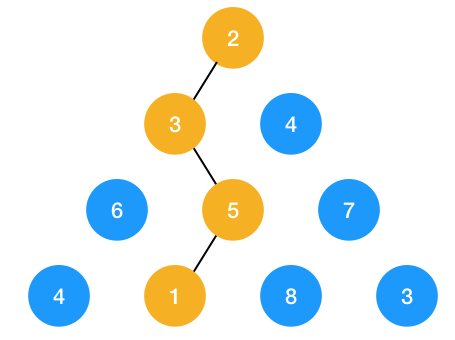
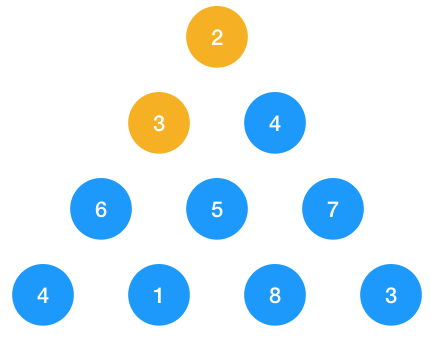
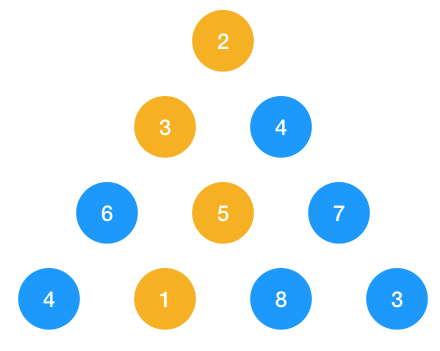
1、 第一步：由 2 往下走，由于 3 比 4 小，所以選擇 3

 

2、 第二步：由 3 往下走，由于 5 比 6 小，所以選擇 5

 

第三步: 從 5 往下走， 1 比 8 小，選擇 1

 

答案是 11 ，與動態規劃得出的解一模一樣!那是否說明這道題可以用貪心算法求解?

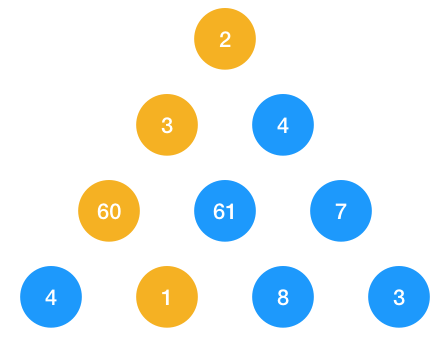
答案是否定的!上面的解之所以是正確的，是因為這些數字恰好按貪心求解出來得出了全局最優解，如果我們換一下數字，看看會如何

 

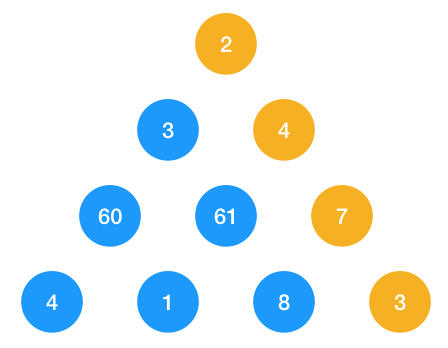
如圖示，如果數字換成如圖中所示，則按貪心得出的最短路徑是 66, 而實際上最短路徑應該為 16，如下圖所示

 

為啥用貪心行不通呢，因為貪心追求的是每一步眼前的最優解，一旦它作出了選擇，就會影響后面子問題的選擇，比如如果選擇了 3，就再也沒法選擇 7 了!所以再次強調，一定要注意貪心的適用場景，子問題之間是否相互制約，相互影響!

總結

本文簡單講述了貪心算法的適用場景，相信大家對貪心的優劣性應該有了比較清晰的認識，貪心追求的是眼前最優解(要最好的，就現在!)不管這次選擇對后面的子問題造成的影響，所以貪心求得解未必是全局最優解，這就像我們做職業規劃一樣，千萬不可因為一時的利益只考慮當下的利益，要作出對長遠的職業生涯能持續有益的選擇， 所以貪心的使用場景比較小，它是動態規劃的特例，所以如果能用貪心來解的也都可以用動態規劃來解。