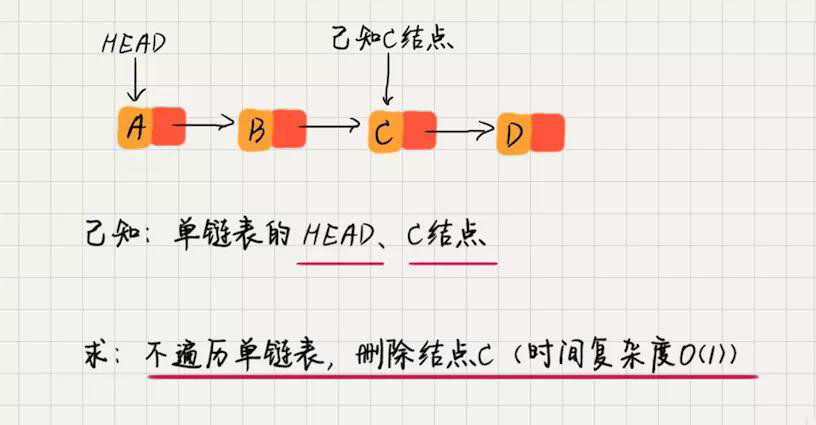
圖解:單鏈表刪除,不遍歷鏈表也能做(時間復雜度O(1))
在開始這個問題之前,先想想,如果給定單鏈表中的某個結點,如何在單鏈表中刪除該節點?
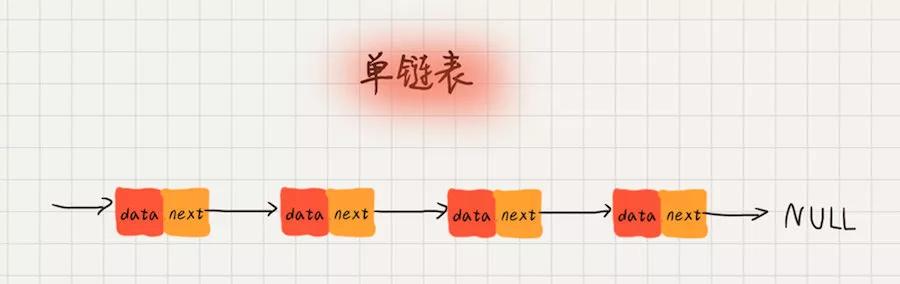
對于一個單鏈表,它每個結點的數據結構除了存儲自身的數據之外,還需要記錄鏈表上,下一個結點的地址,通常我們將這個地址稱之為后續指針 next。
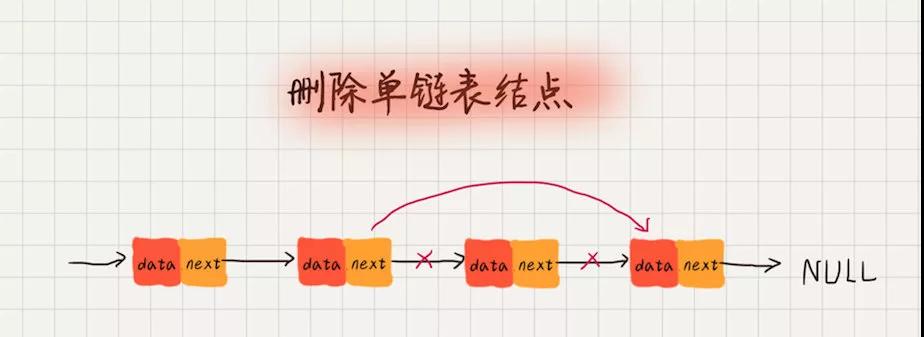
那如上圖所示,我想刪除其中的 C 結點,需要做什么操作?很簡單,將 B 結點的后續指針 next 指向 D 結點即可。
此處應該清晰了,要刪除鏈表上的某個結點,我們需要知道三個結點:
- 待刪除的結點。
- 待刪除結點的前驅結點。
- 待刪除結點的后續結點。
思路:實際刪除下一個結點
再來回顧最開始的問題,當我們已知某個結點的時候,它的后續結點我們也是知道的。唯一的問題,就是他的前驅結點我們不知道。
最簡單的解決方法,就是將鏈表遍歷一遍,獲得待刪除結點的前驅結點,對其進行操作。
當涉及到遍歷鏈表的時候,時間復雜度妥妥的變成 O(n),這就與題不符了。
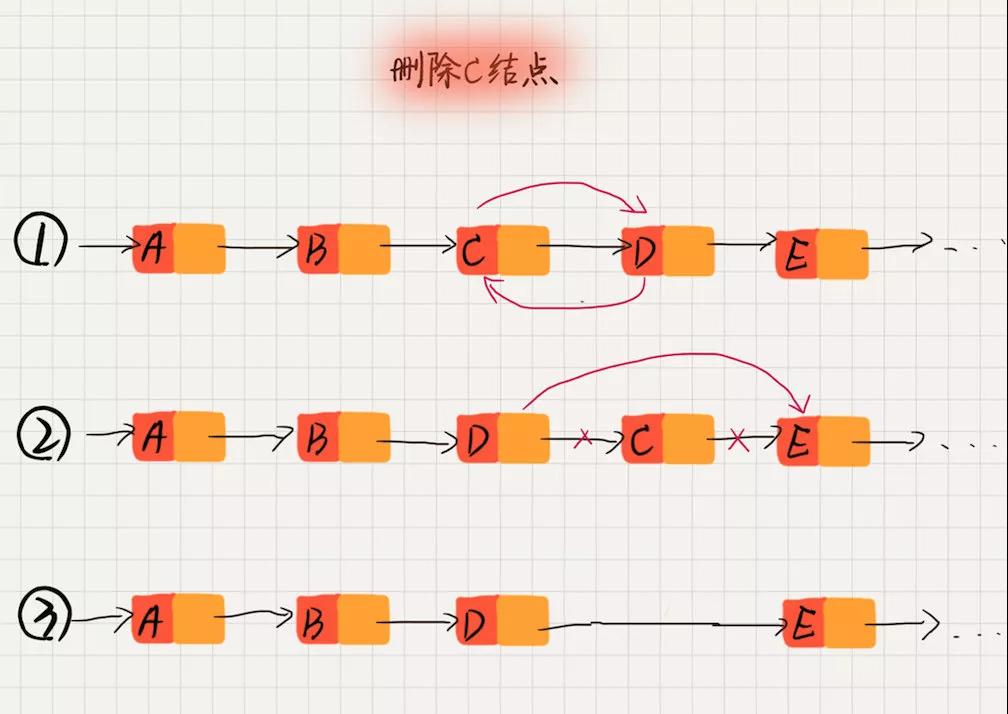
而問題主要卡在了,我們如何知道待刪除結點的前驅結點。試著換一個思路想想,我們只需要刪除該結點存儲的數據,而并不是刪除該結點對應地址中的內容。
那么就可以將待刪除結點的數據,和它的后續結點的數據進行互換,然后對它的后續結點進行刪除操作,以此來達到 O(1) 時間復雜度的單鏈表刪除。
問題:待刪除節點是***一個節點
這個思路還存在一個問題,我們實際刪除的是待刪除節點的下一個節點。還記得前面說,刪除單鏈表中的某個結點,實際上是需要知道三個結點的。
那么,如果刪除的結點,是單鏈表的***一個結點,怎么辦?
這時我們仍然需要從鏈表的頭結點開始遍歷,得到待刪除節點的前驅節點,并完成刪除操作,時間復雜度恢復到 O(n)。
而題目要求我們需要在 O(1) 的時間復雜度內完成刪除操作,這樣是不是不符合題目要求呢?
其實不然,假設單鏈表總共有 n 個節點,這種算法在 n-1 的情況下時間復雜度都是 O(1),只有在待刪除結點為單鏈表的***一個結點時,時間復雜度才會恢復到 O(n),那么平均時間復雜度 [(n-1)*O(1)+O(n)]/n,計算下來仍然為 O(1)。
【本文為51CTO專欄作者“張旸”的原創稿件,轉載請通過微信公眾號聯系作者獲取授權】