知道自己寫的程序的時間復雜度，有利于我們寫出能夠高效運行的程序。

程序是由一個個函數組成的，有些簡單的由幾個基礎運算組成的函數大家一眼就能看出來它的時間復雜度，但是大部分函數沒那么簡單，只要函數里面涉及到了循環、外部函數調用甚至遞歸的時候它的時間復雜度就沒那么容易分析啦。

這篇文章的內容，可以幫你快速推導出程序代碼的時間復雜度。

要分析程序的時間復雜度，首先還是要確定時間復雜度的度量標準— —英文文檔里通常會用 metric 這個單詞來表示，這個標準規定了在函數中平鋪展開的代碼、循環中的代碼、有函數調用的代碼、以及遞歸調用的代碼的時間復雜度的測量方式。

Big O Notations

如何計算程序的時間復雜度呢？最常用的度量方式叫做 Big O Notations 翻譯過來叫大O標記法。

使用大O標記法前要先了解它的幾個要點：

• 相同配置的計算機進行一次基本運算的時間是一定的，因此我們將程序基本運算的執行次數作為時間復雜度的衡量標準。
• 時間復雜度是對運行次數的錯略估計，在計算時可以只考慮對運行時間貢獻大的語句而忽略運行次數少的語句。比如 O(3 * n2 + 10n + 10) 會被統計成 O(n2)。
• 比如有些涉及到排序的程序，執行時間往往依賴于程序的輸入，可以分為最好、最壞、平均情況的時間復雜度，這種時候使用大 O 標記法時我們只用關注最壞的情況，因為最壞情況對衡量程序效率的好壞具有實際意義。

在大O標記法中，常見的時間復雜度有一下幾類。

1. 常數階:常數階的復雜度通常用O(1)表示，不是說程序只有一行基礎代碼運行，它的意思是不管程序的輸入是什么程序都會運行一個固定數量的運算，這個數可以是任何常數5、100、200都行，重點是他不會隨輸入的增長才被統計稱 O(1)
2. 多項式階：很多算法的時間復雜度是 O(n)、O(n2)、O(n3)這樣的多項式。
3. 指數階：指數階的時間復雜度用O(2n) 、 O(nn) 等表示，這種程序運行效率極差，是程序員寫代碼一定要避開的大坑。
4. 對數階：對數階的程序運行效率較高，通常用O(logn)、 O(n log n) 等表示。

它們的關系如下：

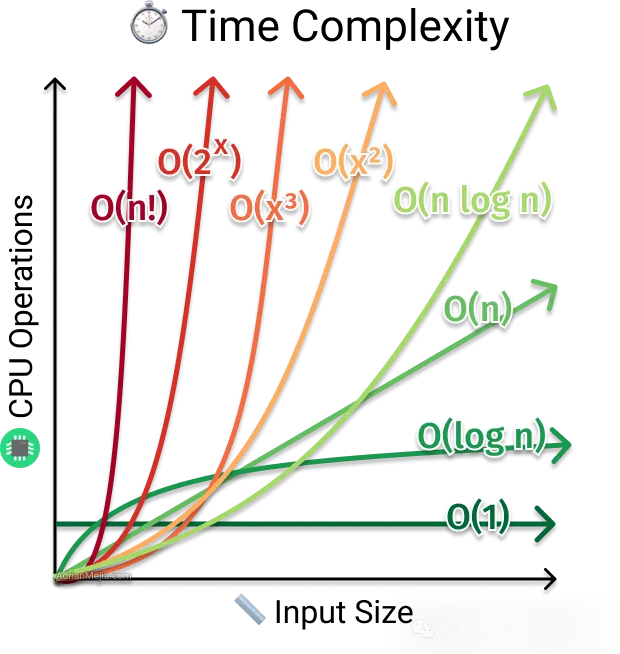圖片

從上面的圖我們可以看到，O(1)是最高效最穩定的，完全不受輸入數據尺寸增長的影響，指數階隨著輸入的增加而爆增，而對數階則增長緩慢。

按照時間復雜度從低到高排序：

O(1) < O(logn) < O(n) < O(n log n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)

在寫程序時，我們要注意時間復雜度增量的問題，盡量避免爆炸級增長。

了解完時間復雜度的大O標記法后，接下來我們看下怎么把我們平時接觸的代碼轉化為其對應的時間復雜度。

順序語句的復雜度

這是最簡單的代碼結構，比如說我們有一個下面的計算3個數字的平方和的函數。

function squareSum(a, b, c) {
  const sa = a * a;
  const sb = b * b;
  const sc = c * c;
  const sum = sa + sb + sc;
  return sum;
}

函數中的每個語句都是一個基本運算。每行的時間復雜度為 O(1)。我們把所有語句的時間加起來，它仍然是 O(1)， 記住昂，不是O(3)。

O(1)表示程序時常數級的時間復雜度，不管程序的輸入是什么程序都會運行數量固定的操作。

注意如果順序排列的代碼中有對函數的調用，復雜度就不是O(1)了，你想知道是多少？

條件語句的復雜度

很少有會有程序代碼沒有任何條件語句。因為大 O 標記法關注程序運行的的最壞情況，所以對一個類似這樣的條件語句：

if (isValid) {
  statement1;
  statement2;
} else {
  statement3;
}

它的時間復雜度可以按下面這個公式推導出來：

T(n) = Math.max([t(statement1) + t(statement2)], [time(statement3)])

比如說下面這個代碼：

if (isValid) {
  array.sort();
  return true;
} else {
  return false;
}

if代碼塊中的時間復雜度為O( n log n) — 常用編程語言內置排序算法的時間復雜度，else代碼塊的時間復雜度為O(1)，那么整個代碼的時間復雜度為：

O([n log n] + [n]) => O(n log n)

循環語句的復雜度

線性循環

for (let i = 0; i < array.length; i++) {
  statement1;
  statement2;
}

對于這個例子，循環執行 array.length次，所有與輸入數據增長而成比例增長的循環都具有線性—常數階的時間復雜度 O(n)。

對數循環

觀察下面的程序：

function fn(n) {
  i = 1;
  while( i < n) {
     i = i*2;
  }
 }

對于這個程序，我們無法確定while 以及 i = i*2 語句運行了多少次，這時可以假設運行了x次，每次運行后i的值為2、22、23… 當while 語句的條件不滿足即i = n時結束，也就是2x = n ， x = log2n ，它的時間復雜度近似于O(logn )。

固定次數循環

for (let i = 0; i < 4; i++) {
  statement1;
  statement2;
}

針對固定條件的循環，像上面這個程序一樣，無聊時固定循環4次還是 100 次時間復雜度都是 O(1)。

嵌套循環

for (let i = 0; i < n; i++) {
  statement1;

  for (let j = 0; j < m; j++) {
    statement2;
    statement3;
  }
}

假設循環中的語句都是基礎操作，沒有對函數的調用，那么這個代碼有兩層嵌套循環，時間復雜度為O(n2)。

循環中有函數調用的時間復雜度

假如我們有這樣一個程序：

for (let i = 0; i < n; i++) {
  fn1();
  for (let j = 0; j < n; j++) {
    fn2();
    for (let k = 0; k < n; k++) {
      fn3();
    }
  }
}

根據 fn1、fn2 和 fn3 函數自身的時間復雜度，整個程序將擁有不同的運行時間。

如果這三個函數它們都是常數階 O(1)，那么最終的運行時間將為 O(n3)。但是如果只有 fn1 和 fn2 是常數介， fn3 的時間復雜度為 O(n2)，則該程序的運行時間將為 O(n5)。

一般來說，循環中有函數調用，時間復雜度可以用下面這個公式計算：

T(n) = n * [ t(fn1()) + n * [ t(fn2()) + n * [ t(fn3()) ] ] ]

函數遞歸調用的時間復雜度

function fn(n) {
 if (n == 1 || n == 2) {
   return 1;
 }
 return fn(n - 1) + fn(n - 2);
}

以上是學算法都學過的斐波那切數列的遞歸調用實現版本，它的時間復雜度為O(2n) ，所以在平時寫代碼時在你不確定程序能執行多少次的時候，最好不要輕易使用遞歸調用。

總結

這篇內容我們梳理了一下不同的時間復雜對大概對應什么樣的代碼，讓我們能更正確地估算自己寫的程序的時間復雜度。