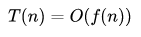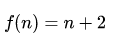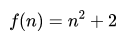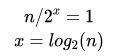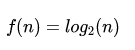算法時間復雜度分析:大O表示法
在開發的時候,我們如何評估一個算法的好壞,如何描述一個算法運行效率的高低呢?通俗一點的表達方法就是程序執行快或慢,但是這只是一種較為寬泛的描述,我們如何直觀科學的用的描述它呢?
有同學可能會說,用其運行時間不就可以很好很直觀的描述它了。不過,不同的語言,不同的編譯器,不同的CPU來說,對程序的處理的時間是不同的,我們無法單單用運行時間來描述某個算法執行效率。另外,當需要處理的數據增長時,算法的基本操作要重復執行的次數也會增長,對于不同的算法的增長的速度也不一樣。
數學果然是個不錯的工具,為了描述算法的運行時間的增長情況,我們可以用不同數學公式來分析。在計算機科學上,我們是有專門的術語來表征算法的效率,就是今天要和大家一起學習的大O表示法。大O并不是表示算法運行需要多長時間,它表示的是算法運行時間的增速,即算法的運行時間以不同的速度增加,也叫漸進時間復雜度。
我們可以用下面的表達式來表示:
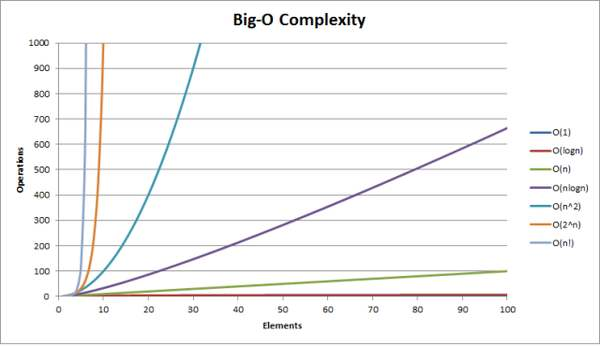
通常主要有以下幾種表達式來描述時間復雜度:
- O(1):常量時間
- O(n):線性時間
- O(log n):對數時間
- O(n^2):二次方時間
- O(2^n):指數時間
- O(n!):階乘時間
每種時間復雜度有所不同,下面我們一起來詳細了解這幾種時間復雜度。
大O復雜度
O(1)
O(1)表示常量時間復雜度,當給定大小為n的輸入,無論n為何值,最后算法執行的時間是個常量。舉個例子:
- int func(int n)
- {
- n++;
- return n*2;
- }
上面的程序中,無論輸入n的值如何變化,程序執行時間始終是個常量。我們簡化處理一下,假如函數中每行語句的執行時間是1,則執行時間的數學表達式:
無論n為多大,最后的執行時間都是2這個固定值。雖然是運行時間為2,但是這里我們也用O(1)來表示,這里的1代表是一個常數。
O(n)
O(n)表示線性時間復雜度,算法的執行時間隨著輸入n的大小成線性變化。
- int func(int n)
- {
- int sum = 0;
- for(int i=0; i<n; i++)
- {
- sum = sum + i;
- }
- return sum;
- }
上面的這個程序中,函數的執行時間隨著n的變化成線性的關系。
對于這種可以用線性表達式表示的情況,我們用O(n)來表示。
為什么可以省略掉表達式中的其他系數呢?主要是當n趨近于無窮大時,系數相對于無窮大的n來說可以忽略不計。
O(n^2 )
O(n^2)表示二次方時間復雜度,一個算法的時間將會隨著輸入數據n的增長而呈現出二次關系增加。
- int func(int n)
- {
- int sum = 0;
- for(int i=0; i<n; i++)
- {
- for(int j=0; j<n; j++)
- {
- sum = sum + i + j;
- }
- }
- return sum;
- }
上面的程序中,是個兩層循環的程序,函數的執行時間和n是二次方的關系:
對于這種類型的程序,我們可以用O(n^2)表示。不過,循環嵌套除了這種兩層循環之外,還會有三層、四層...n層循環,對應的其復雜度就是O(n^3) 、O(n^4)...O(n^n)。
O(2^n)
O(2^n)表示指數復雜度,隨著n的增加,算法的執行時間成倍增加,它是一種爆炸式增長的情況。
- int func(int n)
- {
- if(n==0) return 1;
- return func(n) + func(n-1)
- }
上面的代碼中,有兩次遞歸調用,函數的執行時間就會和輸入n成指數的關系。
因此,這里我們可以用O(2^n)表示。
O(log n)
O(log n)表示對數時間復雜度,算法執行時間和n是一種對數關系。這種類型的算法會在執行的過程中,隨著程序的執行其完成某個功能的操作步驟越來越少。其中,我們所熟知的二分查找法就是一個很好的例子。比如,下面這個代碼在一個有序列表中查找某個值的位置,我們通過二分法進行查找。
- int func(int a[], int size, int num)
- {
- int left = 0;
- int right = size-1;
- while(left <= right)
- {
- int mid = (left + right)/2;
- if(a[mid] > num)
- {
- right = mid - 1;
- }
- else if (a[mid] < num)
- {
- left = mid + 1;
- }
- else
- {
- return num;
- }
- }
- return -1;
- }
在最糟糕的情況下,我們通過二分法拆分x次后,最后一個元素就是我們要找的元素。我們可以得到下面的等式:
函數運行時間可以表示為:
因此,這里我們可以用O(log n)表示。
O(n!)
對于階乘關系的復雜度,最典型的例子就是旅行商問題。
假設有一個旅行商人要拜訪n+1個城市,他必須選擇所要走的路徑,路徑的限制是每個城市只能拜訪一次,而且最后要回到原來出發的城市。路徑的選擇目標是要求得的路徑長度為所有路徑之中的最小值。
這個問題最簡單的方法是通過窮舉法列出所有的排列組合。如果有n+1個城市,根據我們數學中學過的排列組合計算方法,可以算出所有組合數為n!,所以這種窮舉法對應的時間復雜度也就是O(n!)了。
本文轉載自微信公眾號「Will的大食堂」,可以通過以下二維碼關注。轉載本文請聯系Will的大食堂公眾號。