不能忘記!數據科學家面試時應該掌握的3個編程概念
算法是數據科學不可分割的一部分。雖然很多數據科學家在學習的時候沒有選修合適的算法課程,但它確實很重要。
比如說,許多公司在面試數據科學家時,都會問到數據結構和算法。
那么,現在問題是,問數據科學家這樣的問題到底有什么用。
對于這個問題,我的答案是,數據結構問題可以被當作是對編碼能力的測試。
我們都在人生的不同階段接受過能力測試,但是這些測試并不能完美地評判一個人,幾乎沒有什么測試能做到這一點。
那么,為什么不用一個標準算法測試來評判一個人的編碼能力呢?
因為算法和測試都并非死板,你總能在前者總結的基礎上不斷改進、創新,總能運用不同的算法來回應這些測試。
但這也并不意味著你可以不掌握基礎就可以肆意動搖算法的地基。
牢固掌握基礎算法的概念和運用,永遠是一個優秀數據科學家必備的素質。
本文將以一種容易理解的方式幫助數據科學家快速回顧相關研究并介紹一些基本算法概念。
1. 遞歸/記憶化
遞歸是將定義的函數應用到自己的定義中。簡而言之,遞歸是函數的自身調用。當你用谷歌搜索遞歸時,會遇到點小插曲。
剛開始學習數據科學的人可能會覺得遞歸有點難,但其實它很容易理解。一旦理解了,就會發現這是一個很棒的概念。
解釋遞歸的最好例子就是計算一個數的階乘。
- def factorial(n):
- if n==0:
- return 1
- return n*factorial(n-1)
可以很容易地看出階乘是一個遞歸函數。
- Factorial(n) = n*Factorial(n-1)
那么如何將它轉化為編程呢?
遞歸調用的函數通常由兩部分組成:
- 基線條件——終止遞歸的條件。
- 遞歸公式——向基線條件發展的公式。
許多問題解決到最后,就是遞歸問題。這也適用于數據科學。
例如,一棵決策樹是二叉樹,樹算法通常是遞歸的。或者,以我們經常使用的排序為例。排序的算法稱為歸并排序(mergesort),它本身就是一種遞歸算法。另一種是對分查找 (binary search),包括在數組中查找元素。
現在我們了解了遞歸的基本知識,接下來試著找到第n個斐波那契數。斐波那契數列是一系列數字,其中每個數字(斐波那契數)都是前面兩個數字之和。最簡單的數列是1、1、2、3、5、8等。要找到第n個斐波那契數,可以用如下代碼:
- def fib(n):
- if n<=1:
- return 1
- return fib(n-1) + fib(n-2)
但是,發現問題了嗎?
如果試圖計算fib(n=7)要運行兩次fib(5) ,運行三次 fib(4) ,運行5次 fib(3)。隨著n越來越大,對同一數字進行了多次調用,遞歸函數對其進行了一次又一次的計算。
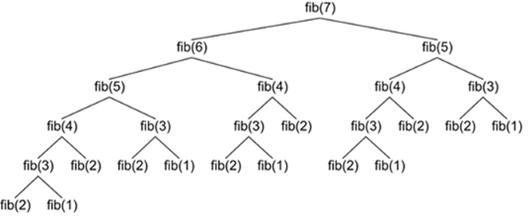
稍微改變我們的執行,添加一個詞典來為這個方法添加一些存儲。現在,每次計算出一個數字,這個備忘錄詞典就會更新。如果再出現同樣的數字,就不需要再對它進行計算,而是可以直接從備忘錄字典中得出結果。這種增加存儲的方式被稱為記憶化。
- memo = {}def fib_memo(n): if n in memo: return memo[n] if n<=1: memo[n]=1 return 1 memo[n] = fib_memo(n-1) +fib_memo(n-2) return memo[n]
通常,我會先寫遞歸代碼,如果它重復調用相同的參數,我會再添加一個詞典來進行記憶化。
這幫助大嗎?
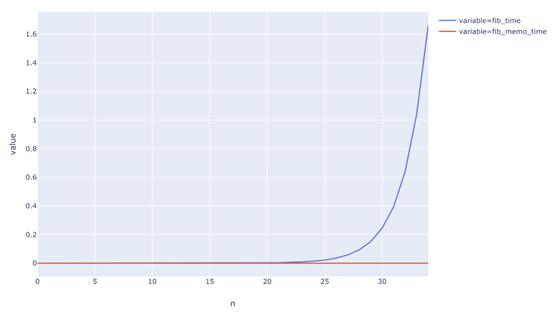
圖中是不同n值的運行時間的比較。可以看到:沒有記憶化的斐波那契函數運行時間呈指數性增長,而記憶化函數的運行時間則是線性的。
2. 動態規劃
遞歸本質就是一種自上而下的方法。比如在計算斐波那契數n時,就是從n開始,然后對n-2和n-1進行遞歸調用,依此類推。
在動態規劃中,我們采取自下而上的方法。這本質上是一種迭代編寫遞歸的方法。首先計算fib(0)和fib(1),然后使用前面的結果生成新的結果。
- def fib_dp(n):
- dp_sols = {0:1,1:1}
- for i in range(2,n+1):
- dp_sols[i] = dp_sols[i-1] +dp_sols[i-2]
- return dp_sols[n]
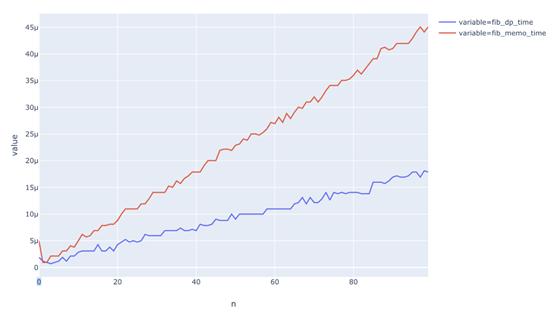
上圖是“動態規劃”和“記憶化”運行時間的比較。可以看出它們都是線性的,但動態規劃更快一點。
為什么呢?因為在這種情況下,動態規劃只對每個子問題進行一次調用。
關于開發動態規劃的貝爾曼是如何選定“動態規劃”這個名字的,有一個很有趣的故事:
“動態規劃”這個名字是從哪里來的呢?20世紀50年代的數學研究情況并不是很好。當時,華盛頓有一位非常有趣的紳士,名叫威爾遜,他是國防部長。實際上,他對研究這個詞懷有病態的恐懼和仇恨。那我能起個什么名字呢?首先,我考慮了“計劃”、“決策”、“思考”。但是出于各種原因,“計劃”并不是一個好詞。于是,我決定使用“規劃”一詞。我想傳遞的概念是,這是動態的,多級的,并且是時變的。因此,我認為動態規劃是個好名字,這可以一舉兩得。這是連國會議員都不會反對的。所以我決定采用這個名字。
3. 二進制搜索
假設有一個排序了的數字組合,要從這個數組中找出一個數字。我們可以采用線性搜索,挨個地檢查每一個數字,直到找到特定數字。問題是,如果數組包含數百萬個元素,這種方法就需要花費很長時間。這種情況下,可以采用二進制搜索方法。
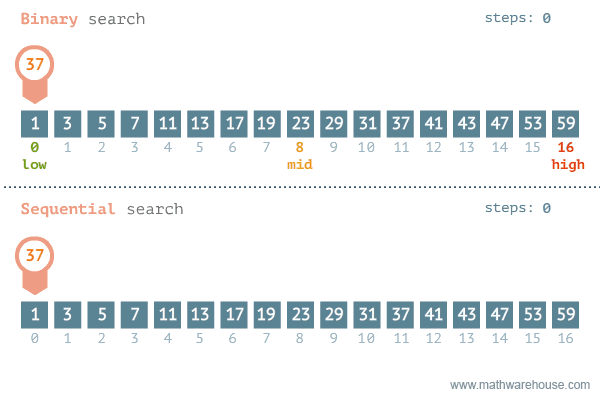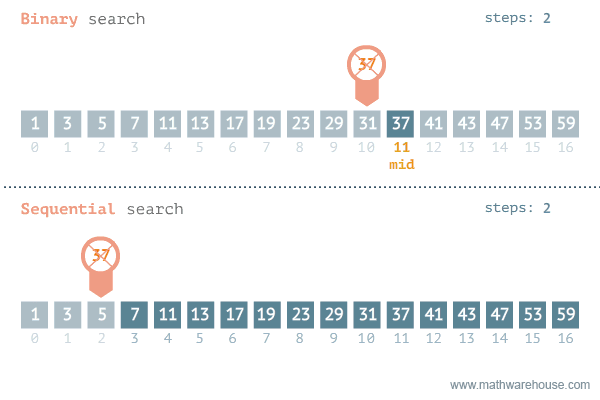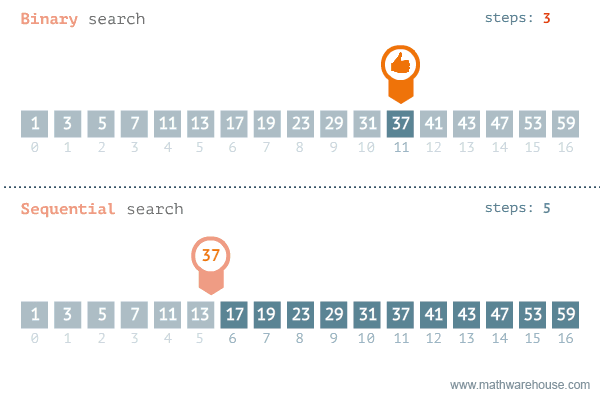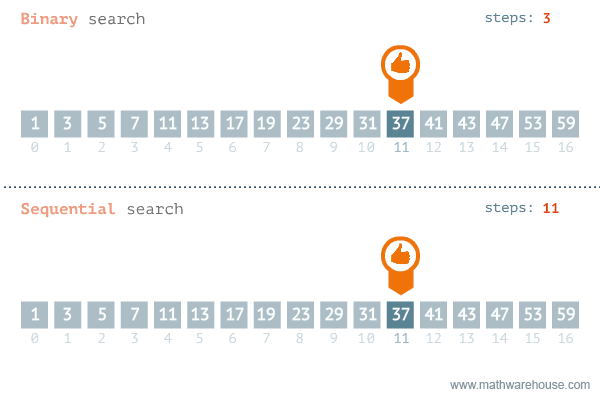
來源:發現37-海洋中有3.7萬億條魚,他們正在尋找其中的1條
- # Returns index of target innums array if present, else -1
- def binary_search(nums, left, right, target):
- # Base case
- if right >= left:
- mid = int((left + right)/2)
- # If target is present at themid, return
- if nums[mid] == target:
- return mid
- # Target is smaller than midsearch the elements in left
- elif nums[mid] > target:
- return binary_search(nums,left, mid-1, target)
- # Target is larger than mid,search the elements in right
- else:
- return binary_search(nums,mid+1, right, target)
- else:
- # Target is not in nums
- return -1nums =[1,2,3,4,5,6,7,8,9]
- print(binary_search(nums, 0, len(nums)-1,7))
這是一個基于遞歸算法的高級例子。利用數組被排序的事實,遞歸地查看中間元素,看看是想在中間元素的左邊還是右邊搜索。這使得每一步的搜索空間減少2倍。
因此,二進制搜索算法的運行時間是O(logn),而不是線性搜索的O(n)。
這有什么作用呢?下面是運行時間的比較。我們可以看到二進制搜索與線性搜索相比是相當快。
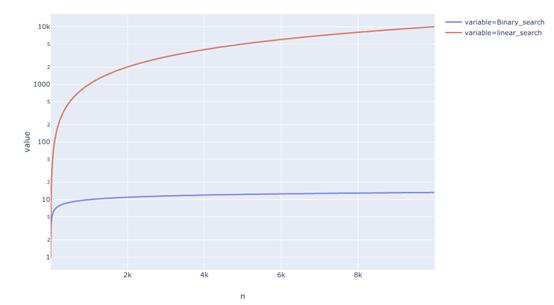
當n=10000時, 二進制搜索需要大約13步,線性搜索需要10000步。
結論
本文談到了一些構成編程基礎的算法,雖然是基礎,但也同樣令人興奮。
數據科學家在面試時會經常被問到這些算法,深入理解它們可能會幫助你找到理想的工作哦。
盡管你不學習這些算法也可以在數據科學中取得進步,但你可以把學習它們當作一種樂趣,培養興趣的同時還可以順便提高編程技能。
一舉兩得,何樂而不為呢?