優化技術何其多也！比如批歸一化、權重標準化……但現有的優化方法大多基于激活或權重執行，最近阿里達摩院的研究者另辟蹊徑，直接對梯度下手，提出全新的梯度中心化方法。只需一行代碼即可嵌入現有的 DNN 優化器中，還可以直接對預訓練模型進行微調。

優化技術對于深度神經網絡 (DNN) 的高效訓練至關重要。以往的研究表明，使用一階和二階統計量（如平均值和方差）在網絡激活或權重向量上執行 Z-score 標準化（如批歸一化 BN 和權重標準化 WS）可以提升訓練性能。

已有方法大多基于激活或權重執行，最近阿里達摩院的研究人員另辟蹊徑提出了一種新型優化技術——梯度中心化（gradient centralization，GC），該方法通過中心化梯度向量使其達到零均值，從而直接在梯度上執行。

我們可以把 GC 方法看做對權重空間和輸出特征空間的正則化，從而提升 DNN 的泛化性能。此外，GC 還能提升損失函數和梯度的 Lipschitz 屬性，從而使訓練過程更加高效和穩定。

GC 的實現比較簡單，只需一行代碼即可將 GC 輕松嵌入到現有基于梯度的 DNN 優化器中。它還可以直接用于微調預訓練 DNN。研究者在不同應用中進行了實驗，包括通用圖像分類和微調圖像分類、檢測與分割，結果表明 GC 可以持續提升 DNN 學習性能。

• 論文地址：https://arxiv.org/pdf/2004.01461.pdf
• 項目地址：https://github.com/Yonghongwei/Gradient-Centralization

不同于基于激活或權重向量運行的技術，該研究提出了一種基于權重向量梯度的簡單而有效的 DNN 優化技術——梯度中心化（GC）。

如圖 1(a) 所示，GC 只是通過中心化梯度向量使其達到零均值。只需要一行代碼，即可將其輕松嵌入到當前基于梯度的優化算法（如 SGDM、Adam）。

盡管簡單，但 GC 達到了多個期望效果，比如加速訓練過程，提高泛化性能，以及對于微調預訓練模型的兼容性。

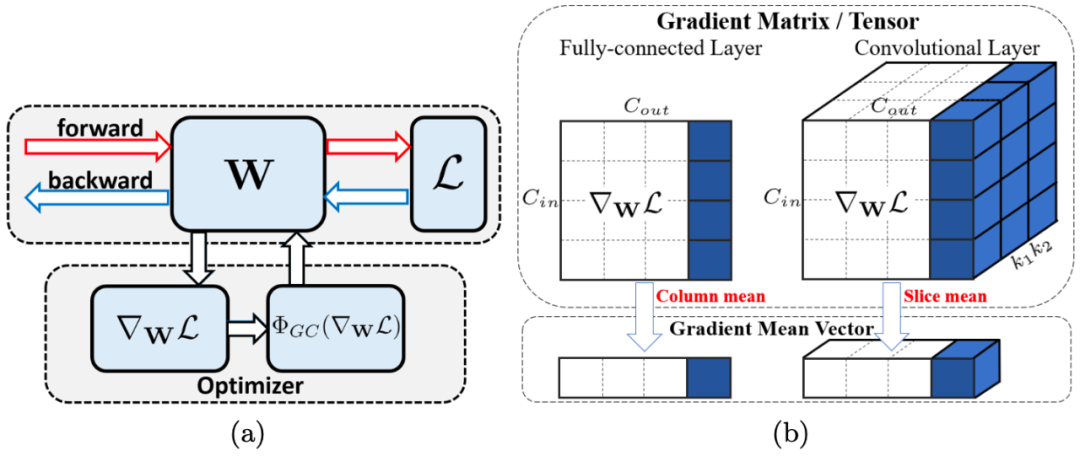
圖 1：(a) 使用 GC 的示意圖。W 表示權重，L 表示損失函數，∇_WL 表示權重梯度，Φ_GC(∇_WL) 表示中心梯度。如圖所示，用 Φ_GC(∇_WL) 替換 ∇_WL 來實現 GC 到現有網絡優化器的嵌入，步驟很簡單。(b) 全連接層（左）和卷積層（右）上梯度矩陣/權重張量的 GC 運算。GC 計算梯度矩陣/張量的每列/slice 的平均值，并將每列/slice 中心化為零均值。

研究貢獻

該研究的主要貢獻有：

• 提出了一種通用網絡優化技術——梯度中心化（GC），GC 不僅能夠平滑和加速 DNN 的訓練過程，還可以提升模型的泛化性能。
• 分析了 GC 的理論性質，指出 GC 通過對權重向量引入新的約束來約束損失函數，該過程對權重空間和輸出特征空間進行了正則化，從而提升了模型的泛化性能。此外，約束損失函數比原始損失函數具備更好的利普希茨屬性，使得訓練過程更加穩定高效。

梯度中心化

研究動機

研究者提出了這樣的疑問：除了對激活和權重的處理外，是否能夠直接對梯度進行處理，從而使訓練過程更加高效穩定呢？一個直觀的想法是，類似于 BN 和 WS 在激活與權重上的操作，使用 Z-score 標準化方法對梯度執行歸一化。不幸的是，研究者發現單純地歸一化梯度并不能提高訓練過程的穩定性。于是，研究者提出一種計算梯度向量均值并將梯度中心化為零均值的方法——梯度中心化。該方法具備較好的利普希茨屬性，能夠平滑 DNN 的訓練過程并提升模型的泛化性能。

GC 公式

對于全連接層或卷積層，假設已經通過反向傳播獲得梯度，那么對于梯度為 ∇_w_i L (i = 1, 2, ..., N ) 的權重向量 w_i，GC 的公式如下所示：

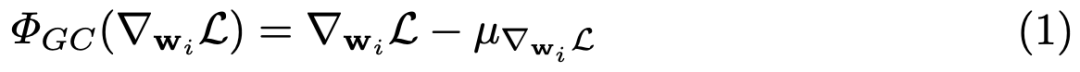
其中

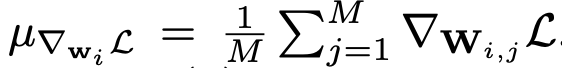
GC 的公式很簡單。如圖 1(b) 所示，只需要計算權重矩陣列向量的平均值，然后從每個列向量中移除平均值即可。

公式 1 的矩陣表述如下所示：

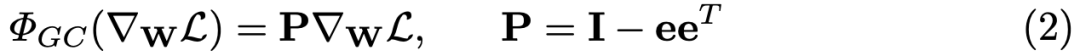
在實際實現中，我們可以從每個權重向量中直接移除平均值來完成 GC 操作。整個計算過程非常簡單高效。

GC 嵌入到 SGDM/Adam 中，效果如何？

GC 可以輕松嵌入到當前的 DNN 優化算法中，如 SGDM 和 Adam。在得到中心化梯度 Φ_GC(∇_wL) 后，研究者直接使用它更新權重矩陣。算法 1 和算法 2 分別展示了將 GC 嵌入兩大最流行優化算法 SGDM 和 Adam 的過程。此外，如要使用權重衰減，可以設置

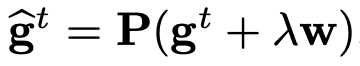
，其中 λ 表示權重衰減因子。

將 GC 嵌入到大部分 DNN 優化算法僅需一行代碼，就可以微小的額外計算成本執行 GC。例如，研究者使用 ResNet50 在 CIFAR100 數據集上進行了一個 epoch 的訓練，訓練時間僅增加了 0.6 秒（一個 epoch 耗時 71 秒）。

GC 的特性

提升泛化性能

我們可以把 GC 看作具備約束損失函數的投影梯度下降方法。約束損失函數及其梯度的利普希茨屬性更優，從而使訓練過程更加高效穩定。

之前的研究已經說明了投影梯度方法的特性，即投影權重梯度將限制超平面或黎曼流形的權重空間。類似地，我們也可以從投影梯度下降的角度看待 GC 的作用。下圖 2 展示了使用 GC 方法的 SGD：

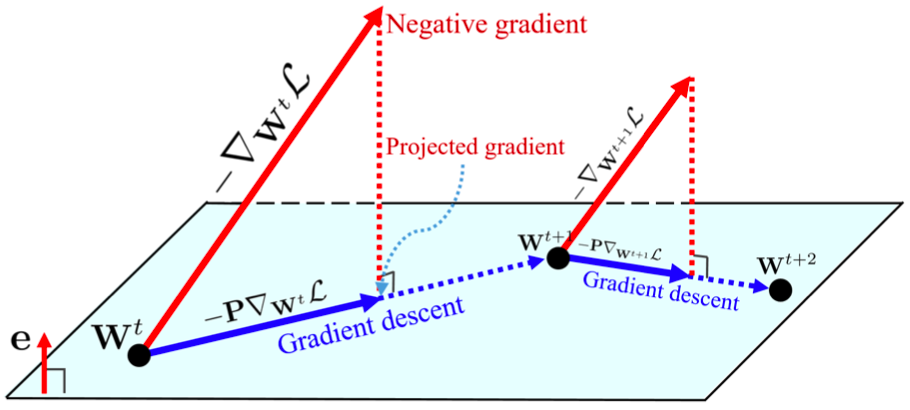
圖 2：GC 方法的幾何解釋。梯度被投影在超平面 e^T (w − w^t) = 0 上，投影梯度被用于更新權重。

加速訓練過程

優化圖景平滑：之前的研究表明 BN 和 WS 可以平滑優化圖景。盡管 BN 和 WS 在激活和權重上執行，但它們隱式地限制了權重梯度，從而使權重梯度在快速訓練時更具預測性，也更加穩定。

類似的結論也適用于 GC 方法，研究者對比了原始損失函數 L(w) 和公式 4 中約束損失函數的利普希茨屬性，以及函數梯度的利普希茨屬性。

梯度爆炸抑制：GC 對于 DNN 訓練的另一個好處是避免梯度爆炸，使訓練更加穩定。這一屬性類似于梯度剪裁。梯度太大會導致權重在訓練過程中急劇變化，造成損失嚴重振蕩且難以收斂。

為了研究 GC 對梯度剪裁的影響，研究者在圖 4 中展示了，在使用和不使用 GC 方法時（在 CIFAR100 上訓練得到的）ResNet50 第一個卷積層和全連接層的梯度矩陣最大值和 L2 范數。從圖中我們可以看到，在訓練過程中使用 GC 方法使得梯度矩陣的最大值和 L_2 范數有所降低。

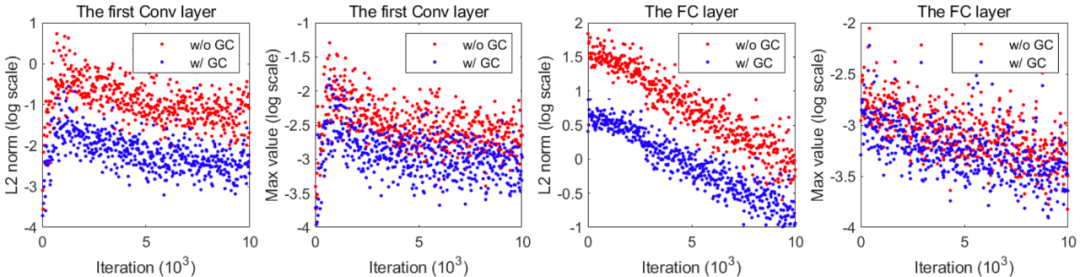
圖 4：梯度矩陣或張量的 L_2 范數（對數尺度）和最大值（對數尺度）隨迭代次數的變化情況。此處使用在 CIFAR100 上訓練得到的 ResNet50 作為 DNN 模型。左側兩幅圖展示了在第一個卷積層上的結果，右側兩幅圖展示了全連接層上的結果。紅點表示不使用 GC 方法的訓練結果，藍點反之。

實驗結果

下圖 5 展示了四種組合的訓練損失和測試準確率曲線。

與 BN 相比，BN+GC 的訓練損失下降得更快，同時測試準確率上升得也更快。對于 BN 和 BN+WS 而言，GC 能夠進一步加快它們的訓練速度。此外，我們可以看到，BN+GC 實現了最高的測試準確度，由此驗證了 GC 能夠同時加速訓練過程并增強泛化性能。

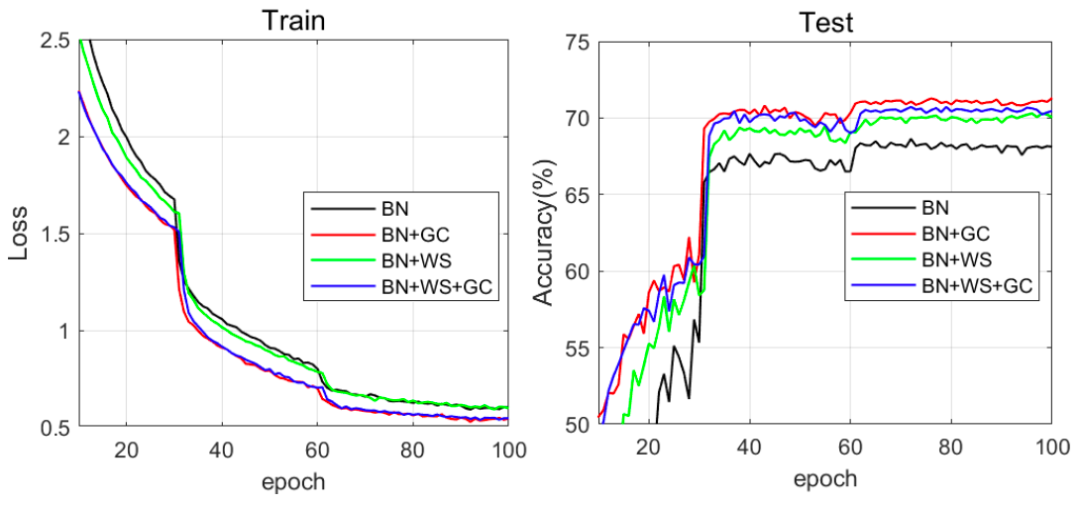
圖 5：在 Mini-ImageNet 數據集上，訓練損失（左）和測試準確率（右）曲線隨訓練 epoch 的變化情況。ResNet50 被用作 DNN 模型。進行對比的優化方法包括 BN、BN+GC、BN+WS 和 BN+WS+GC。

下表 3 展示了不同權重衰減設置下的測試準確率變化，包括 0、1e^-4、2e^-4、5e^-4 和 1e^-3。優化器是學習率為 0.1 的 SGDM。從表中可以看到，權重衰減的性能通過 GC 實現了持續改善。

表 3：在不同權重衰減設置下，使用 ResNet50 在 CIFAR100 數據集上的測試準確率。

下表 4 展示了 SGDM 和 Adam 在不同學習率下的測試準確率變化。

表 4：使用 ResNet50，不同學習率的 SGDM 和 Adam 在 CIFAR100 數據集上的測試準確率。

下圖 6 展示了 ResNet50 的訓練和驗證誤差曲線（GN 被用于特征歸一化）。我們可以看到，借助于 GN，GC 可以大大加速訓練過程。

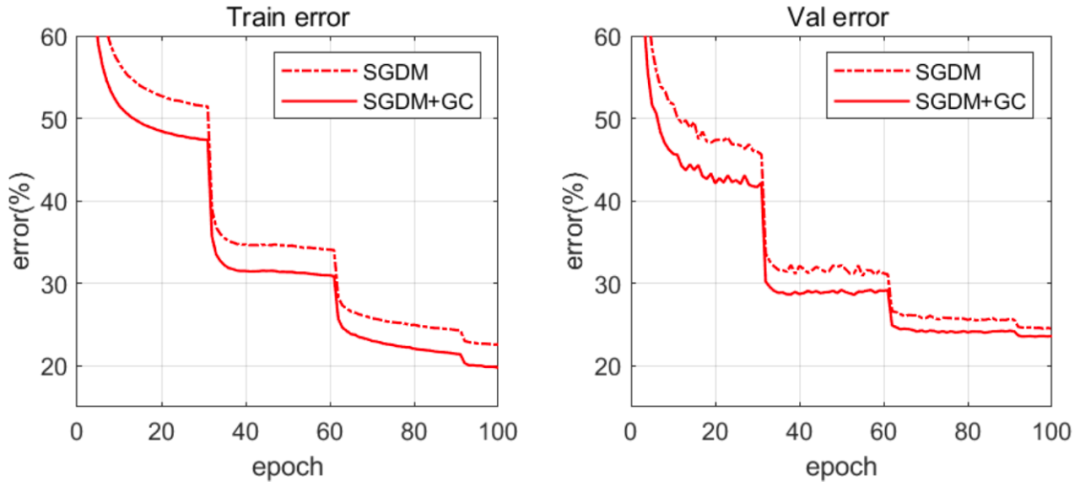
圖 6：在 ImageNet 數據集上，訓練誤差（左）和驗證誤差（右）曲線隨訓練 epoch 的變化情況。

下圖 7 展示了在 4 個細粒度圖像分類數據集上執行前 40 個 epoch 時，SGDM 和 SGDM+GC 的訓練和測試準確率。

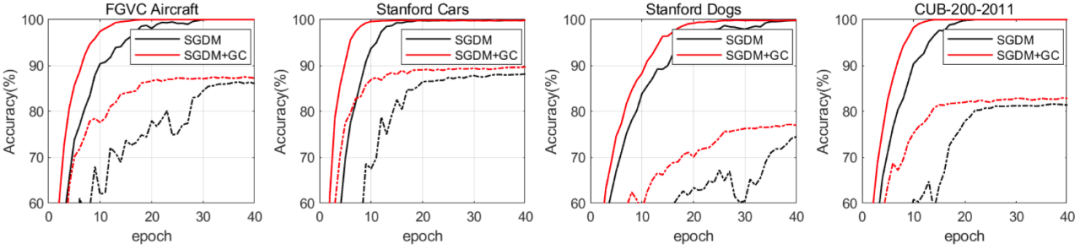
圖 7：在 4 個細粒度圖像分類數據集上，訓練準確率（實線）和測試準確率（虛線）曲線隨訓練 epoch 的變化情況。

下表 8 展示了 Faster R-CNN 的平均精度（Average Precision，AP）。我們可以看到，在目標檢測任務上，使用 GC 訓練的所有骨干網絡均實現了約 0.3%-0.6% 的性能增益。

表 8：使用 Faster-RCNN 和 FPN，不同骨干網絡在 COCO 數據集上的檢測結果。

下表 9 展示了邊界框平均精度（AP^b）和實例分割平均精度（AP^m）。我們可以看到，目標檢測任務上的 AP^b 提升了 0.5%-0.9%，實例分割任務上的 AP^m 提升了 0.3%-0.7%。

表 9：使用 Mask-RCNN 和 FPN，不同骨干網絡在 COCO 數據集上的檢測和分割結果。

使用方法

研究者開源了論文中所提方法，使用 PyTorch 實現。包括 SGD_GC、SGD_GCC、SGDW_GCC、Adam_GC、Adam_GCC、AdamW_GCC 和 Adagrad_GCC 多種優化器，其相應實現在 SGD.py 中提供。后綴為「_GC」的優化器使用 GC 對卷積層和全連接層進行優化，而后綴為「_GCC」的優化器僅可用于卷積層。

而想要使用這些優化器非常簡單，只需使用如下命令 import 對應的模塊即可。

from SGD import SGD_GC  

作者信息

論文一作 Hongwei Yong（雍宏巍）分別在 2013 年和 2016 年取得了西安交通大學的本科與碩士學位，目前是香港理工大學電子計算系博士生。他的主要研究領域包括圖像建模和深度學習等。

[[321808]]

論文一作 Hongwei Yong。

其余三位作者均供職于阿里達摩院，其中 Jianqiang Huang（黃建強）為達摩院資深算法專家，Xiansheng Hua（華先勝）為達摩院城市大腦實驗室負責人，Lei Zhang（張磊）為達摩院城市大腦實驗室高級研究員。