有了K均值聚類,為什么還需要DBSCAN聚類算法?
聚類本文轉載自公眾號“讀芯術”(ID:AI_Discovery)分析是一種無監督學習法,它將數據點分離成若干個特定的群或組,使得在某種意義上同一組中的數據點具有相似的性質,不同組中的數據點具有不同的性質。
聚類分析包括基于不同距離度量的多種不同方法。例如。K均值(點之間的距離)、Affinity propagation(圖之間的距離)、均值漂移(點之間的距離)、DBSCAN(最近點之間的距離)、高斯混合(到中心的馬氏距離)、譜聚類(圖之間距離)等。

2014年,DBSCAN算法在領先的數據挖掘會議ACM SIGKDD上獲得the testof time獎(授予在理論和實踐中受到廣泛關注的算法)。
所有聚類法都使用相同的方法,即首先計算相似度,然后使用相似度將數據點聚類為組或群。本文將重點介紹具有噪聲的基于密度的聚類方法(DBSCAN)。
既然已經有了K均值聚類,為什么還需要DBSCAN這樣的基于密度的聚類算法呢?
K均值聚類可以將松散相關的觀測聚類在一起。每一個觀測最終都成為某個聚類的一部分,即使這些觀測在向量空間中分散得很遠。由于聚類依賴于聚類元素的均值,因此每個數據點在形成聚類中都起著作用。
數據點的輕微變化可能會影響聚類結果。由于聚類的形成方式,這個問題在DBSCAN中大大減少。這通常不是什么大問題,除非遇到一些具有古怪形狀的數據。
使用K均值的另一個困難是需要指定聚類的數量(“k”)以便使用。很多時候不會預先知道什么是合理的k值。
DBSCAN的優點在于,不必指定使用它的聚類數量。需要的只是一個計算值之間距離的函數,以及一些將某些距離界定為“接近”的指令。在各種不同的分布中,DBSCAN也比K均值產生更合理的結果。下圖說明了這一事實:

基于密度的聚類算法
基于密度的聚類是無監督學習法,基于數據空間中的聚類是高點密度的連續區域,通過低點密度的連續區域與其他此類聚類分離,來識別數據中獨特的組/聚類。
具有噪聲的基于密度的聚類方法(DBSCAN)是基于密度聚類的一種基本算法。它可以從大量的數據中發現不同形狀和大小的聚類,這些聚類中正包含著噪聲和異常值。
DBSCAN算法使用以下兩種參數:
- eps (ε):一種距離度量,用于定位任何點的鄰域內的點。
- minPts:聚類在一起的點的最小數目(一個閾值),使一個區域界定為密集。
如果探究兩個稱為密度可達性(DensityReachability)和密度連接性(DensityConnectivity)的概念,就可以理解這些參數。
密度方面的可達性(Reachability)建立了一個可以到達另一個點的點,如果該點位于與另一個點的特定距離(eps)內。
連接性(Connectivity)涉及到基于傳遞性的鏈接方法,以確定點是否位于特定的聚類中。例如,如果p->r->s->t->q,則p和q可以連接,其中a->b表示b在a的鄰域內。
DBSCAN聚類完成后會產生三種類型的點:
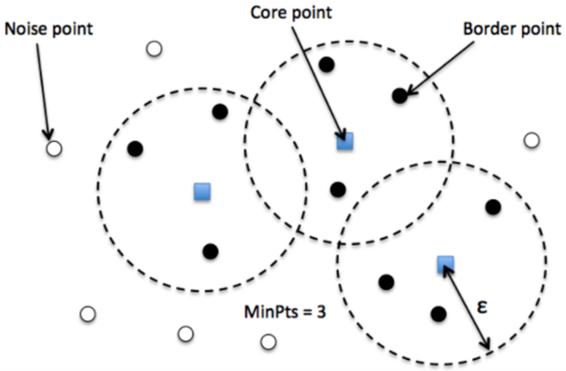
- 核心點(Core)——該點表示至少有m個點在距離n的范圍內。
- 邊界點(Border) ——該點表示在距離n處至少有一個核心。
- 噪聲點(Noise) ——它既不是核心點也不是邊界點。并且它在距離自身n的范圍內有不到m個點。
DBSCAN聚類算法步驟
- 算法通過任意選取數據集中的一個點(直到所有的點都訪問到)來運行。
- 如果在該點的“ε”半徑范圍內至少存在“minPoint”點,那么認為所有這些點都屬于同一個聚類。
- 通過遞歸地重復對每個相鄰點的鄰域計算來擴展聚類
參數估計
每個數據挖掘任務都存在參數問題。每個參數都以特定的方式影響算法。DBSCAN需要參數ε和minPts。
- ε:可以使用k距離圖來選擇ε的值,表示到k=minPts-1最近鄰的距離,從最大值到最小值排序。當此圖顯示“elbow”時,ε值較好:如果ε選擇得太小,則很大一部分數據將無法聚類;如果ε值太高,聚類將合并,同時大多數對象將位于同一聚類中。一般來說,較小的ε值是可取的,根據經驗,只有一小部分點應在此距離內。
- 距離函數:距離函數的選擇與ε的選擇密切相關,對結果有重要影響。通常,在選擇參數ε之前,必須首先確定數據集的合理相似性度量。沒有對此參數的估計,但需要為數據集適當地選擇距離函數。
- minPts:根據經驗,最小minPts可以從數據集中的維度數D導出,即minPts≥D+1。低值minPts=1是沒有意義的,因為此時每個點本身就已經是一個聚類了。當minPts≤2時,結果將與采用單鏈路度量的層次聚類相同,且樹狀圖在高度ε處切割。因此,必須至少選擇3個minPts。
然而,對于有噪聲的數據集,較大的值通常更好,并將產生更顯著的聚類。根據經驗,可以使用minPts=2·dim,但對于非常大的數據、噪聲數據或包含許多重復項的數據,可能需要選擇更大的值。
用sklearn實現DBSCAN python
首先用DBSCAN對球形數據進行聚類。
先生成750個帶有相應標簽的球形訓練數據點。然后對訓練數據的特征進行標準化,最后應用sklearn庫中的DBSCAN。

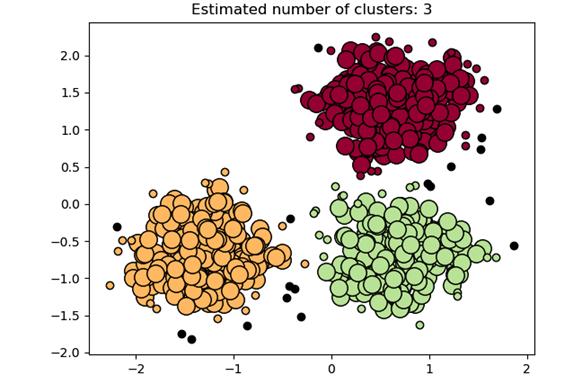
聚類球形數據中的DBSCAN
黑色數據點表示上述結果中的異常值。接下來,用DBSCAN對非球形數據進行聚類。
- import numpy as np
- importmatplotlib.pyplot as plt
- from sklearn import metrics
- fromsklearn.datasets import make_circles
- fromsklearn.preprocessing importStandardScaler
- from sklearn.clusterimportDBSCAN
- X, y =make_circles(n_samples=750, factor=0.3, noise=0.1)
- X=StandardScaler().fit_transform(X)
- y_pred=DBSCAN(eps=0.3, min_samples=10).fit_predict(X)
- plt.scatter(X[:,0], X[:,1], c=y_pred)
- print('Number ofclusters: {}'.format(len(set(y_pred[np.where(y_pred !=-1)]))))
- print('Homogeneity:{}'.format(metrics.homogeneity_score(y, y_pred)))
- print('Completeness:{}'.format(metrics.completeness_score(y, y_pred)))
- print("V-measure:%0.3f"% metrics.v_measure_score(labels_true,labels))
- print("Adjusted RandIndex: %0.3f"
- % metrics.adjusted_rand_score(labels_true,labels))
- print("AdjustedMutual Information: %0.3f"
- % metrics.adjusted_mutual_info_score(labels_true,labels))
- print("SilhouetteCoefficient: %0.3f"
- % metrics.silhouette_score(X, labels))
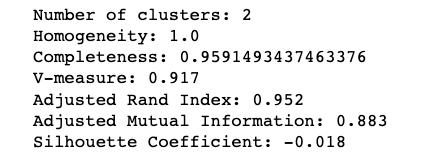
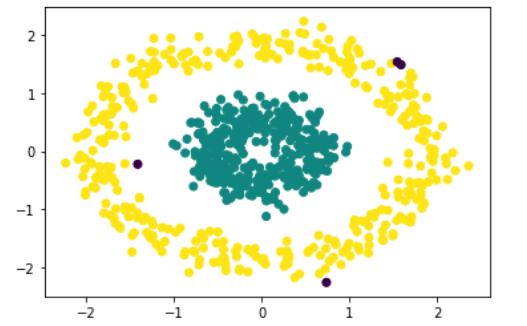
聚類非球形數據中的DBSCAN
這絕對是完美的。如果與K均值進行比較,會給出一個完全不正確的輸出,如:
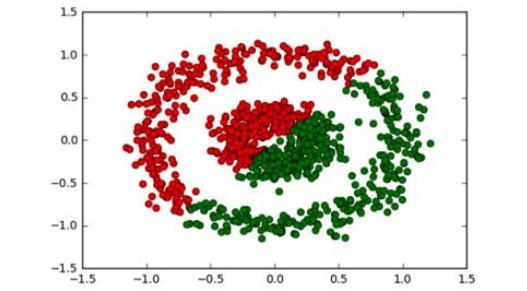
K-均值聚類結果
DBSCAN聚類算法的復雜性
- 平均情況:與最佳/最壞情況相同,取決于數據和算法的實現。
- 最佳情況:如果使用索引系統來存儲數據集,使得鄰域查詢在對數時間內執行,可得到O(nlogn)的平均運行時復雜度。
- 最壞情況:如果不使用索引結構或對退化數據(例如,所有距離小于ε的點),最壞情況下的運行時間復雜度仍為O(n²)。
基于密度的聚類算法可以學習任意形狀的聚類,而水平集樹算法可以在密度差異很大的數據集中學習聚類。
但需要指出的是,這些算法與參數聚類算法(如K均值)相比,調整起來有些困難。與K均值的聚類參數相比,DBSCAN或水平集樹的epsilon參數在推理時不那么直觀,因此為這些算法選擇較好的初始參數值更加困難。










































