Python密度聚類算法-DBSCAN實踐
本文主要內容:
- 前言
- DBSCAN聚類算法
- 參數選擇
- DBSCAN算法迭代可視化展示
- 常用評估方法:輪廓系數
- 用Python實現DBSCAN聚類算法
一、前言
去年學聚類算法的R語言的時候,有層次聚類、系統聚類、K-means聚類、K中心聚類,最后呢,被DBSCAN聚類算法迷上了。
為什么呢,首先它可以發現任何形狀的簇,其次我認為它的理論也是比較簡單易懂的,今年在python這門語言上我打算好好研究DBSCAN。
下面貼上它的官方解釋:
- DBSCAN(Density-Based Spatial Clustering of Applications with Noise,具有噪聲的基于密度的聚類方法)是一種基于密度的空間聚類算法。
- 該算法將具有足夠密度的區域劃分為簇,并在具有噪聲的空間數據庫中發現任意形狀的簇,它將簇定義為密度相連的點的最大集合。
二、DBSCAN聚類算法
文字描述不好懂,先看下面這個圖:
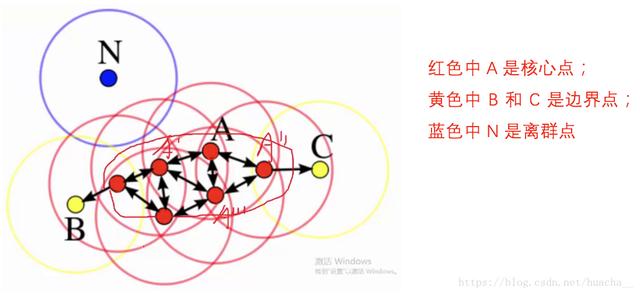
上面這些點是分布在樣本空間的眾多樣本,現在我們的目標是把這些在樣本空間中距離相近的聚成一類。
我們發現A點附近的點密度較大,紅色的圓圈根據一定的規則在這里滾啊滾,最終收納了A附近的5個點,標記為紅色也就是定為同一個簇。
其它沒有被收納的根據一樣的規則成簇。
形象來說,我們可以認為這是系統在眾多樣本點中隨機選中一個,圍繞這個被選中的樣本點畫一個圓,規定這個圓的半徑以及圓內最少包含的樣本點,如果在指定半徑內有足夠多的樣本點在內,那么這個圓圈的圓心就轉移到這個內部樣本點,繼續去圈附近其它的樣本點,類似傳銷一樣,繼續去發展下線。
等到這個滾來滾去的圈發現所圈住的樣本點數量少于預先指定的值,就停止了。那么我們稱最開始那個點為核心點,如A,停下來的那個點為邊界點,如B、C,沒得滾的那個點為離群點,如N)。
基于密度這點有什么好處呢?
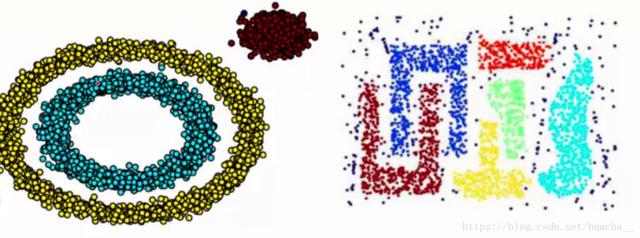
我們知道kmeans聚類算法只能處理球形的簇,也就是一個聚成實心的團(這是因為算法本身計算平均距離的局限)。但往往現實中還會有各種形狀,比如下面兩張圖,環形和不規則形,這個時候,那些傳統的聚類算法顯然就悲劇了。
于是就思考,樣本密度大的成一類唄,這就是DBSCAN聚類算法。
三、參數選擇
上面提到了紅色圓圈滾啊滾的過程,這個過程就包括了DBSCAN算法的兩個參數,這兩個參數比較難指定,公認的指定方法簡單說一下:
半徑:半徑是最難指定的 ,大了,圈住的就多了,簇的個數就少了;反之,簇的個數就多了,這對我們最后的結果是有影響的。我們這個時候K距離可以幫助我們來設定半徑r,也就是要找到突變點,比如: 以上雖然是一個可取的方式,但是有時候比較麻煩 ,大部分還是都試一試進行觀察,用k距離需要做大量實驗來觀察,很難一次性把這些值都選準。
MinPts:這個參數就是圈住的點的個數,也相當于是一個密度,一般這個值都是偏小一些,然后進行多次嘗試
四、DBSCAN算法迭代可視化展示
國外有一個特別有意思的網站,它可以把我們DBSCAN的迭代過程動態圖畫出來。
網址:naftaliharris[1]
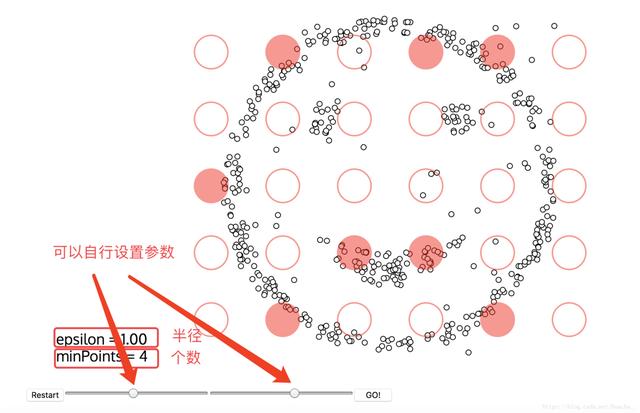
設置好參數,點擊GO! 就開始聚類了!
五、常用評估方法:輪廓系數
這里提一下聚類算法中最常用的評估方法——輪廓系數(Silhouette Coefficient):
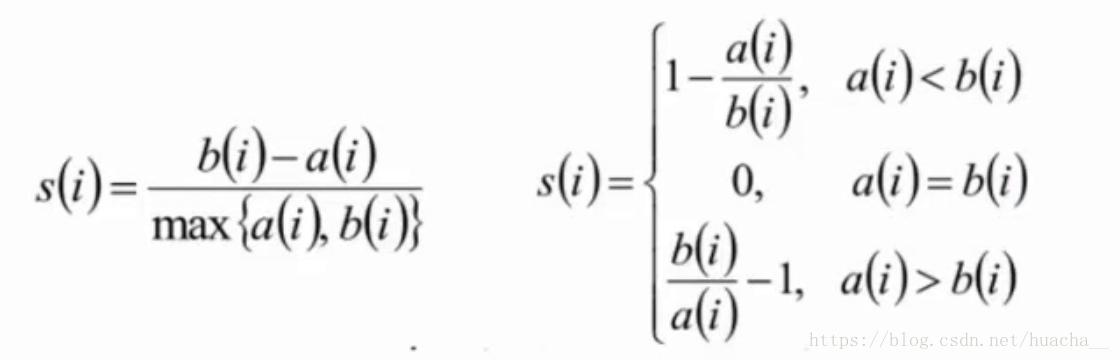
計算樣本i到同簇其它樣本到平均距離ai,ai越小,說明樣本i越應該被聚類到該簇(將ai稱為樣本i到簇內不相似度);
計算樣本i到其它某簇Cj的所有樣本的平均距離bij,稱為樣本i與簇Cj的不相似度。定義為樣本i的簇間不相似度:bi=min(bi1,bi2,...,bik2);
說明:
- si接近1,則說明樣本i聚類合理;
- si接近-1,則說明樣本i更應該分類到另外的簇;
- 若si近似為0,則說明樣本i在兩個簇的邊界上;
六、用Python實現DBSCAN聚類算法
導入數據:
- import pandas as pd
- from sklearn.datasets import load_iris
- # 導入數據,sklearn自帶鳶尾花數據集
- iris = load_iris().data
- print(iris)
輸出:

使用DBSCAN算法:
- from sklearn.cluster import DBSCAN
- iris_db = DBSCAN(eps=0.6,min_samples=4).fit_predict(iris)
- # 設置半徑為0.6,最小樣本量為2,建模
- db = DBSCAN(eps=10, min_samples=2).fit(iris)
- # 統計每一類的數量
- counts = pd.value_counts(iris_db,sort=True)
- print(counts)

可視化:
- import matplotlib.pyplot as plt
- plt.rcParams['font.sans-serif'] = [u'Microsoft YaHei']
- fig,ax = plt.subplots(1,2,figsize=(12,12))
- # 畫聚類后的結果
- ax1 = ax[0]
- ax1.scatter(x=iris[:,0],y=iris[:,1],s=250,c=iris_db)
- ax1.set_title('DBSCAN聚類結果',fontsize=20)
- # 畫真實數據結果
- ax2 = ax[1]
- ax2.scatter(x=iris[:,0],y=iris[:,1],s=250,c=load_iris().target)
- ax2.set_title('真實分類',fontsize=20)
- plt.show()
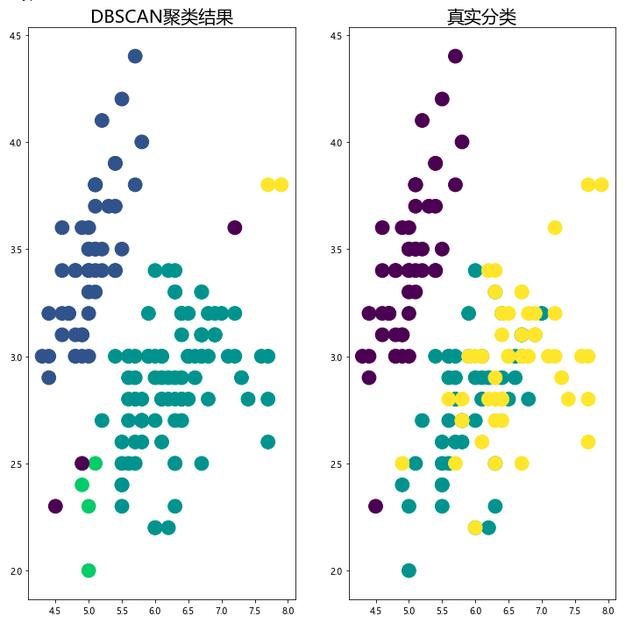
我們可以從上面這個圖里觀察聚類效果的好壞,但是當數據量很大,或者指標很多的時候,觀察起來就會非常麻煩。
這時候可以使用輪廓系數來判定結果好壞,聚類結果的輪廓系數,定義為S,是該聚類是否合理、有效的度量。
聚類結果的輪廓系數的取值在[-1,1]之間,值越大,說明同類樣本相距越近,不同樣本相距越遠,則聚類效果越好。
輪廓系數以及其他的評價函數都定義在sklearn.metrics模塊中,在sklearn中函數silhouette_score()計算所有點的平均輪廓系數。
- from sklearn import metrics
- # 就是下面這個函數可以計算輪廓系數(sklearn真是一個強大的包)
- score = metrics.silhouette_score(iris,iris_db)
- score
結果: 0.364