前言

• BitMap從字面的意思，很多人認(rèn)為是位圖，其實(shí)準(zhǔn)確的來(lái)說(shuō)，翻譯成基于位的映射，怎么理解呢?

問(wèn)題引入

有一個(gè)無(wú)序有界int數(shù)組{1,2,5,7},初步估計(jì)占用內(nèi)存44=16字節(jié)，因?yàn)橹挥?個(gè)數(shù)，很容易，可以很快找到需要的數(shù)。但是假如有10億個(gè)這樣的數(shù)呢，10億個(gè)不重復(fù)并且沒(méi)有排過(guò)序的無(wú)符號(hào)的int整數(shù)，給出一個(gè)整數(shù)，找出給定的某個(gè)數(shù)，你該如何操作?

需求分析：Int類型在Java中的存儲(chǔ)占用4個(gè)Byte,32Bit。10億4/(102410241024)=3.72G左右。如果這樣的一個(gè)大的數(shù)據(jù)做查找和排序，那估計(jì)內(nèi)存也崩潰了，有人說(shuō)，這些數(shù)據(jù)可以不用一次性加載，那就是要存盤(pán)了，存盤(pán)必然消耗IO。我們提倡的是高性能，這個(gè)方案直接不考慮。

[[330308]]

問(wèn)題分析

如果用BitMap思想來(lái)解決的話，就好很多，那么BitMap是怎么解決的啊，如下：

一個(gè)byte是占8個(gè)bit，如果每一個(gè)bit的值就是有或者沒(méi)有，也就是二進(jìn)制的0或者1，如果用bit的位置代表數(shù)組值有還是沒(méi)有，那么0代表該數(shù)值沒(méi)有出現(xiàn)過(guò)，1代表該數(shù)組值出現(xiàn)過(guò)。不也能描述數(shù)據(jù)了嗎?具體如下圖： 

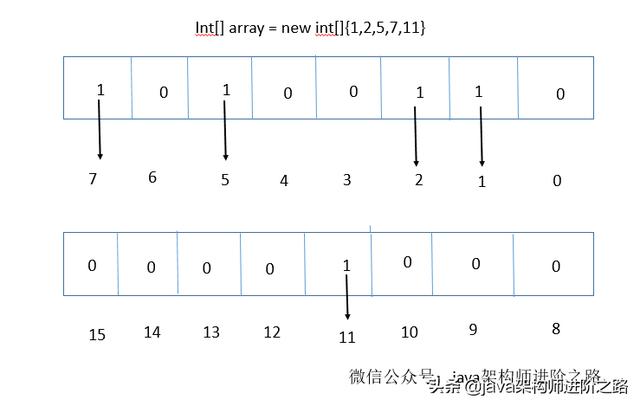
是不是很神奇，那么現(xiàn)在假如10億的數(shù)據(jù)所需的空間就是3.72G/32了吧，一個(gè)占用32bit的數(shù)據(jù)現(xiàn)在只占用了1bit，節(jié)省了不少的空間，排序就更不用說(shuō)了，一切顯得那么順利。這樣的數(shù)據(jù)之間沒(méi)有關(guān)聯(lián)性，要是讀取的，你可以用多線程的方式去讀取。時(shí)間復(fù)雜度方面也是O(Max/n)，其中Max為byte[]數(shù)組的大小，n為線程大小。

三、應(yīng)用與代碼

如果BitMap僅僅是這個(gè)特點(diǎn)，我覺(jué)得還不是它的優(yōu)雅的地方，接下來(lái)繼續(xù)欣賞它的魅力所在。下面的計(jì)算思想其實(shí)就是針對(duì)bit的邏輯運(yùn)算得到，類似這種邏輯運(yùn)算的應(yīng)用場(chǎng)景可以用于權(quán)限計(jì)算之中。

再看代碼之前，我們先搞清楚一個(gè)問(wèn)題，一個(gè)數(shù)怎么快速定位它的索引號(hào)，也就是說(shuō)搞清楚byte[index]的index是多少，position是哪一位。舉個(gè)例子吧，例如add(14)。14已經(jīng)超出byte[0]的映射范圍，在byte[1]范圍之類。那么怎么快速定位它的索引呢。如果找到它的索引號(hào)，又怎么定位它的位置呢。Index(N)代表N的索引號(hào)，Position(N)代表N的所在的位置號(hào)。

• Index(N) = N/8 = N >> 3;
• Position(N) = N%8 = N & 0x07;

(1) add(int num)

你要向bitmap里add數(shù)據(jù)該怎么辦呢，不用擔(dān)心，很簡(jiǎn)單，也很神奇。上面已經(jīng)分析了，add的目的是為了將所在的位置從0變成1.其他位置不變. 

實(shí)例代碼：

public void add(int num){ 
        // num/8得到byte[]的index 
        int arrayIndex = num >> 3;  
         
        // num%8得到在byte[index]的位置 
        int position = num & 0x07;  
         
        //將1左移position后，那個(gè)位置自然就是1，然后和以前的數(shù)據(jù)做|，這樣，那個(gè)位置就替換成1了。 
        bits[arrayIndex] |= 1 << position;  
    } 

(2) clear(int num)

對(duì)1進(jìn)行左移，然后取反，最后與byte[index]作與操作。 

實(shí)例代碼：

public void clear(int num){ 
        // num/8得到byte[]的index 
        int arrayIndex = num >> 3;  
         
        // num%8得到在byte[index]的位置 
        int position = num & 0x07;  
         
        //將1左移position后，那個(gè)位置自然就是1，然后對(duì)取反，再與當(dāng)前值做&，即可清除當(dāng)前的位置了. 
        bits[arrayIndex] &= ~(1 << position);  
 
    } 

(3) contain(int num) 

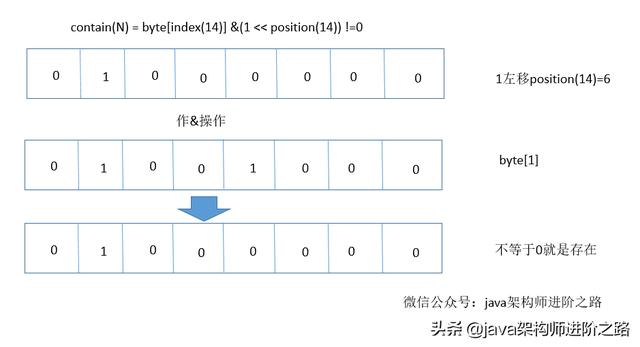
實(shí)例代碼：

public boolean contain(int num){ 
       // num/8得到byte[]的index 
       int arrayIndex = num >> 3;  
        
       // num%8得到在byte[index]的位置 
       int position = num & 0x07;  
        
       //將1左移position后，那個(gè)位置自然就是1，然后和以前的數(shù)據(jù)做&，判斷是否為0即可 
       return (bits[arrayIndex] & (1 << position)) !=0;  
   } 

全部代碼如下：

public class BitMap { 
    //保存數(shù)據(jù)的 
    private byte[] bits; 
     
    //能夠存儲(chǔ)多少數(shù)據(jù) 
    private int capacity; 
     
     
    public BitMap(int capacity){ 
        this.capacity = capacity; 
         
        //1bit能存儲(chǔ)8個(gè)數(shù)據(jù)，那么capacity數(shù)據(jù)需要多少個(gè)bit呢，capacity/8+1,右移3位相當(dāng)于除以8 
        bits = new byte[(capacity >>3 )+1]; 
    } 
     
    public void add(int num){ 
        // num/8得到byte[]的index 
        int arrayIndex = num >> 3;  
         
        // num%8得到在byte[index]的位置 
        int position = num & 0x07;  
         
        //將1左移position后，那個(gè)位置自然就是1，然后和以前的數(shù)據(jù)做|，這樣，那個(gè)位置就替換成1了。 
        bits[arrayIndex] |= 1 << position;  
    } 
     
    public boolean contain(int num){ 
        // num/8得到byte[]的index 
        int arrayIndex = num >> 3;  
         
        // num%8得到在byte[index]的位置 
        int position = num & 0x07;  
         
        //將1左移position后，那個(gè)位置自然就是1，然后和以前的數(shù)據(jù)做&，判斷是否為0即可 
        return (bits[arrayIndex] & (1 << position)) !=0;  
    } 
     
    public void clear(int num){ 
        // num/8得到byte[]的index 
        int arrayIndex = num >> 3;  
         
        // num%8得到在byte[index]的位置 
        int position = num & 0x07;  
         
        //將1左移position后，那個(gè)位置自然就是1，然后對(duì)取反，再與當(dāng)前值做&，即可清除當(dāng)前的位置了. 
        bits[arrayIndex] &= ~(1 << position);  
 
    } 
     
    public static void main(String[] args) { 
        BitMap bitmap = new BitMap(100); 
        bitmap.add(7); 
        System.out.println("插入7成功"); 
         
        boolean isexsit = bitmap.contain(7); 
        System.out.println("7是否存在:"+isexsit); 
         
        bitmap.clear(7); 
        isexsit = bitmap.contain(7); 
        System.out.println("7是否存在:"+isexsit); 
    } 
} 

總結(jié)：

Bitmap典型的應(yīng)用場(chǎng)景為：大量數(shù)據(jù)的快速排序、查找、去重

其被廣泛用于數(shù)據(jù)庫(kù)和搜索引擎中，通過(guò)利用位級(jí)并行，它們可以顯著加快查詢速度。

但是，位圖索引會(huì)占用大量的內(nèi)存，因此我們會(huì)更喜歡壓縮位圖索引。

以上為全部?jī)?nèi)容。