[[335033]]

從決策樹到神經網絡

TL; DR：熵是對系統中混沌的一種度量。 因為它比諸如準確性甚至均方誤差之類的其他更嚴格的度量標準更具動態性，所以使用熵來優化從決策樹到深度神經網絡的算法已顯示出可以提高速度和性能。

它在機器學習中無處不在：從決策樹的構建到深度神經網絡的訓練，熵是機器學習中必不可少的度量。

熵源于物理學-它是系統中無序或不可預測性的量度。 例如，在一個盒子里考慮兩種氣體：一開始，系統的熵很低，因為這兩種氣體是完全可分離的。 但是，一段時間后，氣體混合在一起，系統的熵增加。 有人說，在一個孤立的系統中，熵永遠不會減小，沒有外力，混沌就不會減弱。

例如，考慮一次拋硬幣-如果拋硬幣四次而發生事件[尾巴，頭，頭，尾]。 如果您(或機器學習算法)要預測下一次硬幣翻轉，則可以確定地預測結果-系統包含高熵。 另一方面，具有事件[尾巴，尾巴，尾巴，尾巴]的加權硬幣的熵極低，并且根據當前信息，我們幾乎可以肯定地說下一個結果將是尾巴。

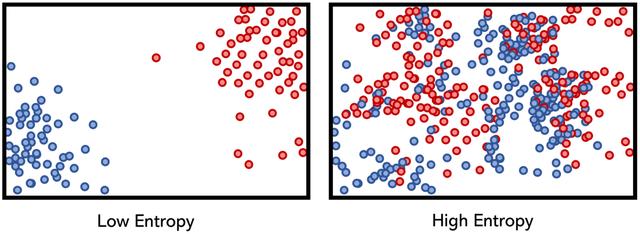
適用于數據科學的大多數情況都介于天文學的高熵和極低的熵之間。 高熵意味著低信息增益，而低熵意味著高信息增益。 可以將信息獲取視為系統中的純凈性：系統中可用的純凈知識量。

決策樹在其構造中使用熵：為了盡可能有效地將一系列條件下的輸入定向到正確的結果，將熵較低(信息增益較高)的特征拆分(條件)放在樹上較高位置。

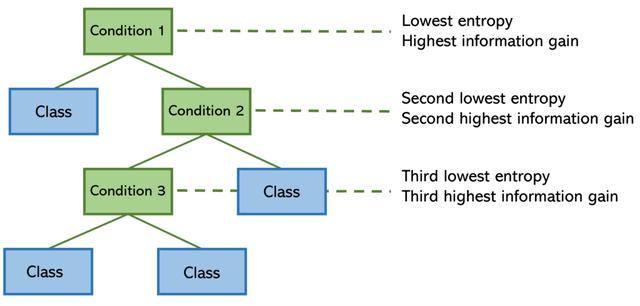
為了說明低熵條件和高熵條件的概念，請考慮假設類特征，其類別用顏色(紅色或藍色)標記，而拆分用垂直虛線標記。

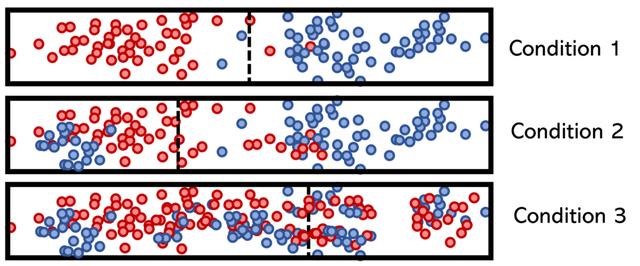
決策樹計算特征的熵并對其進行排列，以使模型的總熵最小(并使信息增益比較大)。 從數學上講，這意味著將最低熵條件放在頂部，以便它可以幫助降低其下方的拆分節點的熵。

決策樹訓練中使用的信息增益和相對熵定義為兩個概率質量分布p(x)和q(x)之間的"距離"。 也稱為Kullback-Leibler(KL)散度或Earth Mover的距離，用于訓練對抗性網絡以評估生成的圖像與原始數據集中的圖像相比的性能。

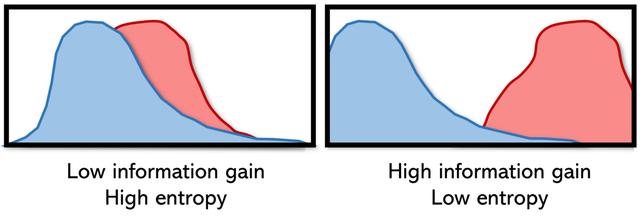
神經網絡最喜歡的損失函數之一是交叉熵。 無論是分類的，稀疏的還是二進制的交叉熵，該度量標準都是高性能神經網絡的默認損耗函數之一。 它也可以用于幾乎所有分類算法的優化，例如邏輯回歸。 像熵的其他應用(例如聯合熵和條件熵)一樣，交叉熵是對熵進行嚴格定義的多種口味之一，適合于獨特的應用。

像Kullback-Lieber發散(KLD)一樣，交叉熵也處理兩個分布p和q之間的關系，分別表示真實分布p和近似分布q。 但是，KLD衡量兩個分布之間的相對熵，而交叉熵衡量兩個分布之間的"總熵"。

度量定義為使用模型分布q對來自分布p的源的數據進行編碼所需的平均位數。 如果考慮目標分布p和近似值q，我們希望減少使用q而不是p表示事件所需的位數。 另一方面，相對熵(KLD)衡量從分布q中的p表示事件所需的額外位數。

交叉熵似乎是衡量模型性能的一種回旋方式，但是有幾個優點：

• 基于準確性/錯誤的指標存在多個問題，包括對訓練數據順序的極端敏感性，不考慮置信度，并且對可能導致錯誤結果的各種數據屬性缺乏魯棒性。 它們是非常粗略的績效指標(至少在培訓期間)。
• 交叉熵可以衡量信息內容，因此比簡單強調所有復選框的度量標準更具動態性和可靠性。 預測和目標被視為分布，而不是等待回答的問題列表。
• 它與概率的性質密切相關，并且特別適用于S型和SoftMax激活(即使它們僅用于最后一個神經元)，有助于減少消失的梯度問題。 邏輯回歸可以視為二進制交叉熵的一種形式。

盡管熵并不總是最佳的損失函數(尤其是在目標函數p尚未明確定義的情況下)，但熵通常表現為性能增強，這說明了熵在任何地方都存在。

通過在機器學習中使用熵，它的核心組成部分(不確定性和概率)可以通過交叉熵，相對熵和信息增益等思想得到很好的體現。 熵對于處理未知數非常明確，這在模型構建中非常需要。 當模型在熵上進行優化時，它們能夠以增強的知識和目標意識在不可預測的平原上徘徊。