讀取黃金 ETF 數據

本文使用機器學習方法來預測最重要的貴金屬之一黃金的價格。我們將創建一個線性回歸模型，該模型從過去的黃金 ETF (GLD) 價格中獲取信息，并返回對第二天黃金 ETF 價格的預測。GLD是直接投資實物黃金的最大ETF。（掃描本文最下方二維碼獲取全部完整源碼和Jupyter Notebook 文件打包下載。）

首先要做的是：導入所有必要庫。 

# LinearRegression 是一個用于線性回歸的機器學習庫  
from sklearn.linear_model import LinearRegression  
# pandas 和 numpy 用于數據操作  
import pandas as pd  
import numpy as np  
# matplotlib 和 seaborn 用于繪制圖形  
import matplotlib.pyplot as plt  
%matplotlib inline  
plt.style.use('seaborn-darkgrid')  
# yahoo Finance用于獲取數據  
import yfinance as yf 

然后，我們讀取過去 12 年的每日黃金 ETF 價格數據并將其存儲在 Df 中。我們刪除不相關的列并使用 dropna() 函數刪除 NaN 值。然后，我們繪制黃金 ETF 收盤價。 

Df = yf.download('GLD', '2008-01-01', '2020-6-22', auto_adjust=True)  
DfDf = Df[['Close']]  
DfDf = Df.dropna()  
Df.Close.plot(figsize=(10, 7),color='r')  
plt.ylabel("Gold ETF Prices")  
plt.title("Gold ETF Price Series")  
plt.show() 

定義解釋變量

解釋變量是一個被操縱以確定第二天黃金 ETF 價格的變量。簡單地說，它們是我們想要用來預測黃金 ETF 價格的特征。

該策略中的解釋變量是過去 3 天和 9 天的移動平均線。我們使用 dropna() 函數刪除 NaN 值并將特征變量存儲在 X 中。

但是，您可以向 X 添加更多您認為對預測黃金 ETF 價格有用的變量。這些變量可以是技術指標、其他 ETF 的價格，例如黃金礦工 ETF (GDX) 或石油 ETF (USO)，或美國經濟數據。

定義因變量

同樣，因變量取決于解釋變量的值。簡而言之，這是我們試圖預測的黃金 ETF 價格。我們將黃金 ETF 價格存儲在 y 中。 

Df['S_3'] = Df['Close'].rolling(window=3).mean()  
Df['S_9'] = Df['Close'].rolling(window=9).mean() 
Df['next_day_price'] = Df['Close'].shift(-1)  
DfDf = Df.dropna()  
X = Df[['S_3', 'S_9']]  
y = Df['next_day_price'] 

將數據拆分為訓練和測試數據集

在這一步中，我們將預測變量和輸出數據拆分為訓練數據和測試數據。通過將輸入與預期輸出配對，訓練數據用于創建線性回歸模型。

測試數據用于估計模型的訓練效果。

 •前 80% 的數據用于訓練，剩余的數據用于測試

  •X_train & y_train 是訓練數據集

   •X_test & y_test 是測試數據集 

t = .8  
t = int(t*len(Df))  
XX_train = X[:t]  
yy_train = y[:t]  
XX_test = X[t:]  
yy_test = y[t:] 

創建線性回歸模型

我們現在將創建一個線性回歸模型。但是，什么是線性回歸？

如果我們試圖捕捉“x”和“y”變量之間的數學關系，通過對散點圖擬合一條線，“最好”根據“x”的觀察值解釋“y”的觀察值，那么這樣的方程 x 和 y 之間的關系稱為線性回歸分析。

為了進一步分解，回歸用自變量解釋了因變量的變化。因變量“y”是您要預測的變量。自變量“x”是您用來預測因變量的解釋變量。以下回歸方程描述了這種關系： 

Y = m1 * X1 + m2 * X2 + C  
Gold ETF price = m1 * 3 days moving average + m2 * 15 days moving average + c  

然后我們使用擬合方法擬合自變量和因變量（x 和 y）以生成回歸系數和常數。 

linear = LinearRegression().fit(X_train, y_train)  
print("Linear Regression model")  
print("Gold ETF Price (y) = %.2f * 3 Days Moving Average (x1) \  
+ %.2f * 9 Days Moving Average (x2) \  
+ %.2f (constant)" % (linear.coef_[0], linear.coef_[1], linear.intercept_)) 

輸出線性回歸模型:

黃金 ETF 價格 (y) = 1.20 * 3 天移動平均線 (x1) + -0.21 * 9 天移動平均線 (x2) + 0.43（常數）

預測黃金ETF價格

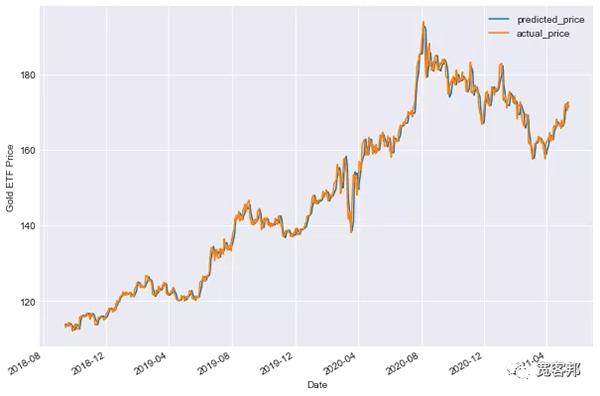
現在，是時候檢查模型是否在測試數據集中工作了。我們使用使用訓練數據集創建的線性模型來預測黃金 ETF 價格。預測方法找到給定解釋變量 X 的黃金 ETF 價格 (y)。 

predicted_price = linear.predict(X_test)  
predicted_price = pd.DataFrame(  
    predicted_price, index=y_test.index, columns=['price'])  
predicted_price.plot(figsize=(10, 7))  
y_test.plot()  
plt.legend(['predicted_price', 'actual_price'])  
plt.ylabel("Gold ETF Price")  
plt.show() 

該圖顯示了黃金 ETF 的預測價格和實際價格。

現在，讓我們使用 score() 函數計算擬合優度。 

r2_score = linear.score(X[t:], y[t:])*100  
float("{0:.2f}".format(r2_score)) 

輸出：

99.21

可以看出，模型的 R 平方為 99.21%。R 平方始終介于 0 和 100% 之間。接近 100% 的分數表明該模型很好地解釋了黃金 ETF 的價格。

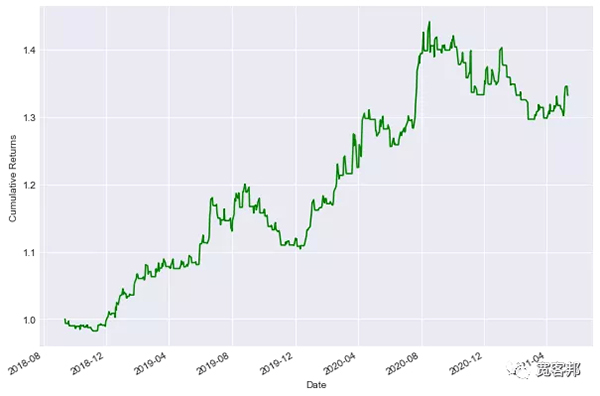
繪制累積收益

讓我們計算一下這個策略的累積收益來分析它的表現。

累計收益計算步驟如下：

•  生成黃金價格的每日百分比變化

•  當第二天的預測價格高于當天的預測價格時，創建一個以“1”表示的買入交易信號

•  通過將每日百分比變化乘以交易信號來計算策略回報。

•  最后，我們將繪制累積收益圖 

gold = pd.DataFrame()  
gold['price'] = Df[t:]['Close']  
gold['predicted_price_next_day'] = predicted_price  
gold['actual_price_next_day'] = y_test  
gold['gold_returns'] = gold['price'].pct_change().shift(-1)  
gold['signal'] = np.where(gold.predicted_price_next_day.shift(1) < gold.predicted_price_next_day,1,0)  
gold['strategy_returns'] = gold.signal * gold['gold_returns']  
((gold['strategy_returns']+1).cumprod()).plot(figsize=(10,7),color='g')  
plt.ylabel('Cumulative Returns')  
plt.show() 

輸出如下：

我們還將計算夏普比： 

sharpe = gold['strategy_returns'].mean()/gold['strategy_returns'].std()*(252**0.5)  
'Sharpe Ratio %.2f' % (sharpe)  

輸出如下：

'Sharpe Ratio 1.06'

預測每日價格

您可以使用以下代碼來預測黃金價格，并給出我們應該購買 GLD 還是不持倉的交易信號： 

import datetime as dt  
current_date = dt.datetime.now()  
data = yf.download('GLD', '2008-06-01', current_date, auto_adjust=True)  
data['S_3'] = data['Close'].rolling(window=3).mean()  
data['S_9'] = data['Close'].rolling(window=9).mean()  
datadata = data.dropna()  
data['predicted_gold_price'] = linear.predict(data[['S_3', 'S_9']])  
data['signal'] = np.where(data.predicted_gold_price.shift(1) < data.predicted_gold_price,"Buy","No Position")  
data.tail(1)[['signal','predicted_gold_price']].T 

輸出如下：