排序是每個 IT 工程師和開發人員必備的知識技能。不僅要通過編程面試，而且要了解算法本身。不同的排序算法很好地展示了算法設計如何對程序的復雜性、速度和效率產生如此大的影響。

讓我們來看看排名前5，也是最常見，面試中經常被問到的排序算法，看看如何用Python實現它們!

1.冒泡排序

冒泡排序是 CS 入門課程中最常講授的一種，因為它清楚地說明了排序的工作原理，同時又簡單又易于理解。冒泡排序將逐步遍歷列表并比較相鄰的元素對。如果元素的順序錯誤，則會交換這些元素。重復對列表中未排序部分的遍歷，直到對列表進行排序。因為冒泡排序重復地通過列表中未排序的部分，所以它的最壞情況復雜性為O(n²)。

def bubble_sort(arr): 
    def swap(i, j): 
        arr[i], arr[j] = arr[j], arr[i] 
 
    n = len(arr) 
    swapped = True 
     
    x = -1 
    while swapped: 
        swapped = False 
        x = x + 1 
        for i in range(1, n-x): 
            if arr[i - 1] > arr[i]: 
                swap(i - 1, i) 
                swapped = True 
                     
    return arr 

2.選擇排序

選擇排序也相當簡單，優于冒泡排序。如果你要在這兩者之間進行選擇，那么最好使用默認的“右選擇排序”。使用選擇排序，我們將輸入列表/數組分為兩部分：已排序項的子列表和構成列表其余部分的剩余項的子列表。

我們首先在未排序的子列表中找到最小的元素，并將其放在已排序子列表的末尾。因此，我們不斷地獲取最小的未排序元素，并將其按排序順序放入已排序的子列表中。此過程將重復進行，直到列表完全排序。

def selection_sort(arr):         
    for i in range(len(arr)): 
        minimum = i 
         
        for j in range(i + 1, len(arr)): 
            # 選擇最小值 
            if arr[j] < arr[minimum]: 
                minimum = j 
 
        # 把它放在已排序的數組結尾 
        arr[minimum], arr[i] = arr[i], arr[minimum] 
             
    return arr 

3.插入排序

插入排序比冒泡排序和選擇排序都要快，而且可以說更加簡單。就像在玩紙牌游戲時，洗牌的過程就是反復進行插入排序!在每次循環迭代中，插入排序從數組中刪除一個元素。然后在另一個排序數組中查找該元素所屬的位置，并將其插入其中。它重復這個過程，直到沒有輸入元素保留。

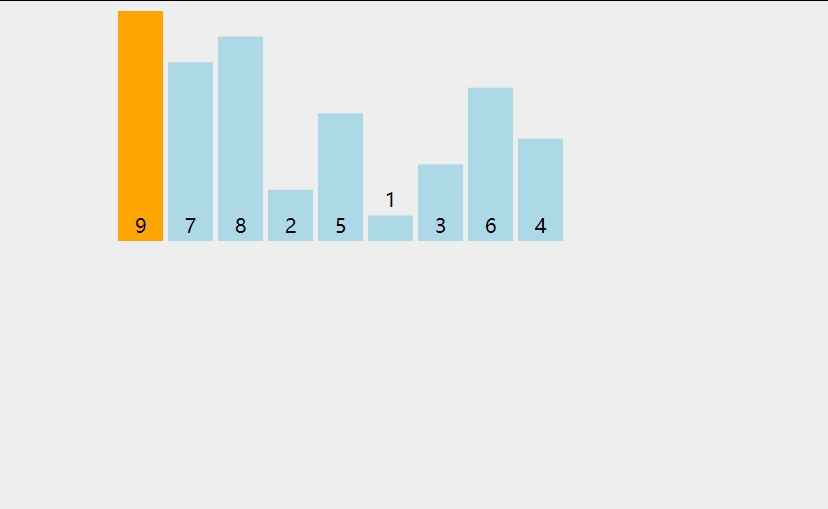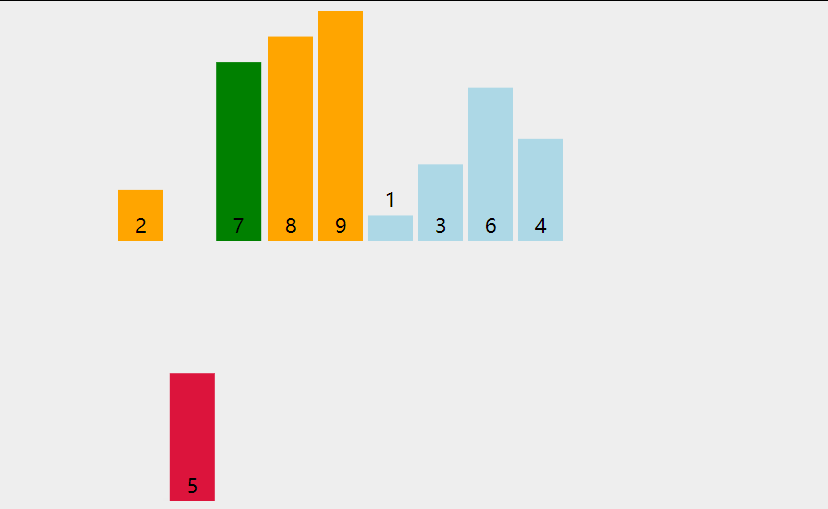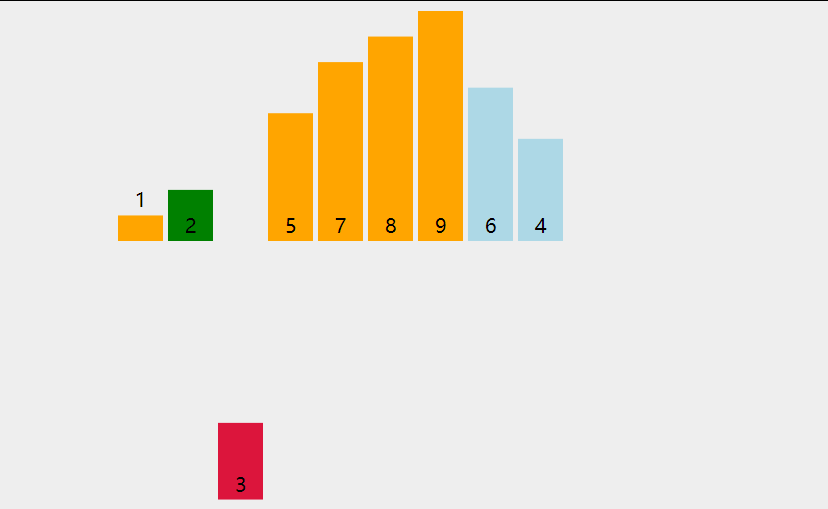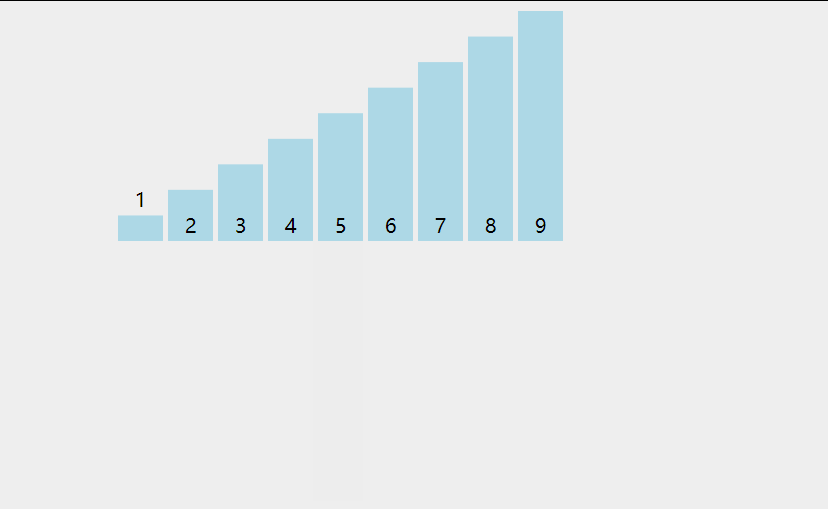
def insertion_sort(arr): 
         
    for i in range(len(arr)): 
        cursor = arr[i] 
        pos = i 
         
        while pos > 0 and arr[pos - 1] > cursor: 
            # 交換列表中的數字 
            arr[pos] = arr[pos - 1] 
            pos = pos - 1 
        # 中斷并進行最終交換 
        arr[pos] = cursor 
 
    return arr 

4.合并排序

合并排序是一個完美的分而治之的算法例子。使用這種算法只需要通過以下兩個主要步驟：

(1) 連續分割未排序的列表，直到有N個子列表，其中每個子列表都有1個“未排序”的元素，N是原始數組中的元素數。

(2) 反復合并，即一次將兩個子列表合并在一起，生成新的已排序子列表，直到所有元素都完全合并到一個已排序的數組中。

def merge_sort(arr): 
    # 對最后一個數組進行拆分 
    if len(arr) <= 1: 
        return arr 
    mid = len(arr) // 2 
    # 在兩個部分上遞歸執行merge_sort 
    left, right = merge_sort(arr[:mid]), merge_sort(arr[mid:]) 
 
    # 合并在一起 
    return merge(left, right, arr.copy()) 
 
 
def merge(left, right, merged): 
 
    left_cursor, right_cursor = 0, 0 
    while left_cursor < len(left) and right_cursor < len(right): 
       
        # 將每一個排序并放入結果 
        if left[left_cursor] <= right[right_cursor]: 
            merged[left_cursor+right_cursor]=left[left_cursor] 
            left_cursor += 1 
        else: 
            merged[left_cursor + right_cursor] = right[right_cursor] 
            right_cursor += 1 
             
    for left_cursor in range(left_cursor, len(left)): 
        merged[left_cursor + right_cursor] = left[left_cursor] 
         
    for right_cursor in range(right_cursor, len(right)): 
        merged[left_cursor + right_cursor] = right[right_cursor] 
 
    return merged 

5.快速排序

快速排序也是一種分而治之的算法，與合并排序一樣。盡管它有點復雜，但在大多數標準實現中，它的執行速度比合并排序快得多，而且很少達到O(n²)的最壞情況復雜度。它有三個主要步驟：

(1) 我們首先從數組中選擇一個元素，稱之為pivot。

(2) 將小于軸的所有元素移到軸的左側;將大于軸的所有元素移到軸的右側。這稱為分區操作。

(3) 遞歸地將上述2個步驟分別應用于元素的每個子數組，這些元素的值比上一個軸的值小或大。

def partition(array, begin, end): 
    pivot_idx = begin 
    for i in xrange(begin+1, end+1): 
        if array[i] <= array[begin]: 
            pivot_idx += 1 
            array[i], array[pivot_idx] = array[pivot_idx], array[i] 
    array[pivot_idx], array[begin] = array[begin], array[pivot_idx] 
    return pivot_idx 
 
def quick_sort_recursion(array, begin, end): 
    if begin >= end: 
        return 
    pivot_idx = partition(array, begin, end) 
    quick_sort_recursion(array, begin, pivot_idx-1) 
    quick_sort_recursion(array, pivot_idx+1, end) 
 
def quick_sort(array, begin=0, end=None): 
    if end is None: 
        end = len(array) - 1 
     
    return quick_sort_recursion(array, begin, end) 

--END--

很多同學在學習 Python 時，都會遇到各種各樣的算法問題，有些很容易就能搞懂，但是有些就需要一些時間精力來學習。

本文中的5種排序算法比較適合 Python 新手，大多數老程序員對排序算法已經爐火純青了，都是在面試過程中，被迫學習的。