您可以整天訓練有監督的機器學習模型，但是除非您評估其性能，否則您永遠無法知道模型是否有用。這個詳細的討論回顧了您必須考慮的各種性能指標，并對它們的含義和工作方式提供了直觀的解釋。

為什么需要評估？

讓我從一個非常簡單的例子開始。

羅賓和山姆都開始為工科大學準備入學考試。他們倆共享一個房間，并在解決數字問題時付出了相同的努力。他們倆全年學習了幾乎相同的時間，并參加了期末考試。令人驚訝的是，羅賓清除了，但薩姆沒有清除。當被問到時，我們知道他們的準備策略有一個區別，即“測試系列”。羅賓加入了一個測試系列，他過去通過參加那些考試來測試他的知識和理解力，然后進一步評估他落后的地方。但是山姆很有信心，他只是不斷地訓練自己。

以相同的方式，如上所述，可以使用許多參數和新技術對機器學習模型進行廣泛的訓練，但是只要您跳過它的評估，就不能相信它。

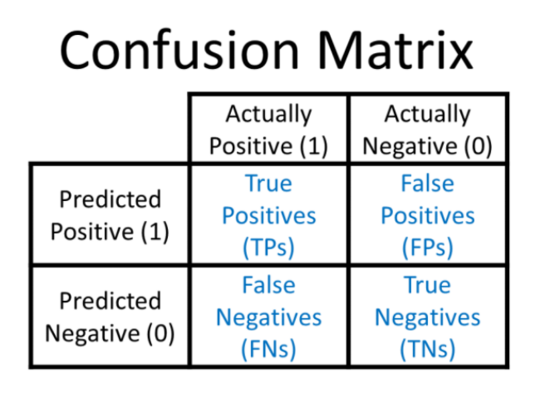
混淆矩陣

混淆矩陣   是一個模型的預測和數據點的實際類別標簽之間的相關性的矩陣。

假設您正在建立一個模型來檢測一個人是否患有糖尿病。進行訓練測試拆分后，您獲得了長度為100的測試集，其中70個數據點標記為正（1），而30個數據點標記為負（0）。現在，讓我為您的測試預測繪制矩陣：

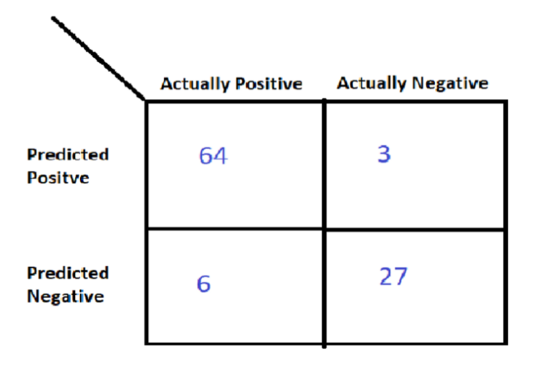
在70個實際的陽性數據點中，您的模型預測64個點為正，6個點為負。在30個實際負點中，它預測3個正點和27個負點。

注意：   在“   真肯定”，“真否定”，“假肯定”和“假否定”表示法中 ，請注意，第二項（“正”或“負”）表示您的預測，而第一項則表示您預測的是對還是錯。

基于上面的矩陣，我們可以定義一些非常重要的比率：

TPR（真正率）=（真正/實際正）

TNR（真負利率）=（真負/實際負）

FPR（誤報率）=（誤報/實際負）

FNR（假負率）=（假負/實際正數）

對于我們的糖尿病檢測模型，我們可以計算以下比率：

TPR = 91.4％

TNR = 90％

FPR = 10％

FNR = 8.6％

如果您希望模型很聰明，那么模型必須正確預測。這意味著您的   “正肯定”  和  “負否定”  應盡可能高 ，同時，您需要將錯誤 肯定  和  錯誤否定 應盡可能少的 錯誤降至最低   。   同樣在比率方面，您的   TPR和TNR  應該很高，   而  FPR和FNR  應該非常低 ，

智能模型：  TPR↑，TNR↑，FPR↓，FNR↓

愚蠢的模型：  TPR，TNR，FPR，FNR的任何其他組合

可能有人爭辯說，不可能平等地照顧所有四個比率，因為最終沒有一種模型是完美的。那我們該怎么辦？

是的，它是真的。因此，這就是為什么我們要建立模型并牢記領域的原因。在某些領域要求我們將特定比率作為主要優先事項，即使以其他比率較差為代價。例如，在癌癥診斷中，我們不能不惜一切代價錯過任何陽性患者。因此，我們應該將TPR保持在最大值，將FNR保持在接近0的水平。即使我們預測有任何健康的患者被診斷出，也仍然可以，因為他可以進行進一步檢查。

準確性

準確度是其字面意思，表示模型的準確度。

準確性=正確的預測/總預測

通過使用混淆矩陣，精度=（TP + TN）/（TP + TN + FP + FN）

準確性是我們可以使用的最簡單的性能指標之一。但是讓我警告您，準確性有時會導致您對模型產生錯誤的幻想，因此您應該首先了解所使用的數據集和算法，然后才決定是否使用準確性。

在討論準確性的失敗案例之前，讓我為您介紹兩種類型的數據集：

1. 平衡的： 一個數據集，包含所有標簽/類別幾乎相等的條目。例如，在1000個數據點中，600個為正，400個為負。

2. 不平衡： 一種數據集，其中包含偏向特定標簽/類別的條目的分布。例如，在1000個條目中，有990個為正面類別，有10個為負面類別。

非常重要：處理不平衡的測試集時，切勿使用準確性作為度量。

為什么？

假設您有一個不平衡的測試集，其中包含 990（+ ve）   和   10（-ve） 的1000個條目  。最終，您以某種方式最終創建了一個糟糕的模型，該模型總是會因列車不平衡而始終預測“ + ve”。現在，當您預測測試集標簽時，它將始終預測為“ + ve”。因此，從1000個測試設定點中，您可以獲得1000個“ + ve”預測。然后你的準確性就會來

990/1000 = 99％

哇！驚人！您很高興看到如此出色的準確性得分。

但是，您應該知道您的模型確實很差，因為它總是預測“ + ve”標簽。

非常重要：同樣，我們無法比較兩個返回概率得分并具有相同準確性的模型。

有某些模型可以像Logistic回歸那樣給出每個數據點屬于特定類的概率。讓我們來考慮這種情況：

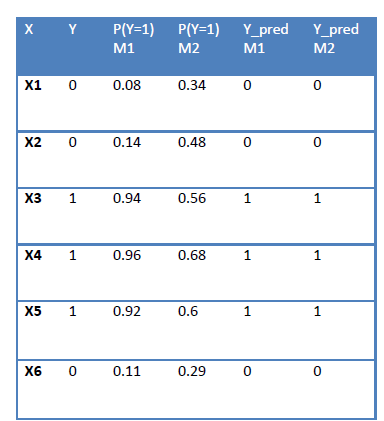
如您所見，   如果P（Y = 1）> 0.5，則預測為類1。   當我們計算M1和M2的精度時，得出的結果相同，但是很明顯，  M1比M2好得多通過查看概率分數。

Log Loss 處理了這個問題  ，我將在稍后的博客中進行解釋。

精度和召回率

精度：   這是真實陽性率（TP）與陽性預測總數的比率。基本上，它告訴我們您的正面預測實際上是正面多少次。

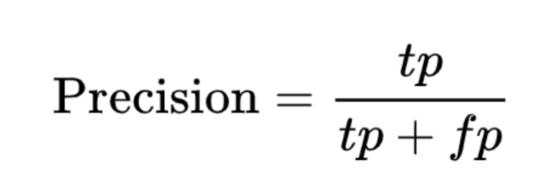
回想一下：   它不過是TPR（上文所述的“真陽性率”）。它告訴我們所有正因素中有多少被預測為正。

F度量：   精確度和查全率的諧波平均值。

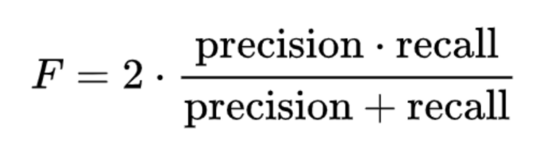
為了理解這一點，讓我們看這個例子：當您在百度中查詢時，它返回40個頁面，但是只有30個相關。但是您的朋友告訴您，該查詢共有100個相關頁面。所以它的精度是30/40 = 3/4 = 75％，而召回率是30/100 = 30％。因此，在這種情況下，精度是“搜索結果的有用程度”，召回率是“結果的完成程度”。

ROC和AUC

接收器工作特性曲線（ROC）：

它是   通過從模型給出的概率得分的反向排序列表中獲取多個閾值而計算出的 TPR（真正率）和FPR（假正率）之間的關系圖 。

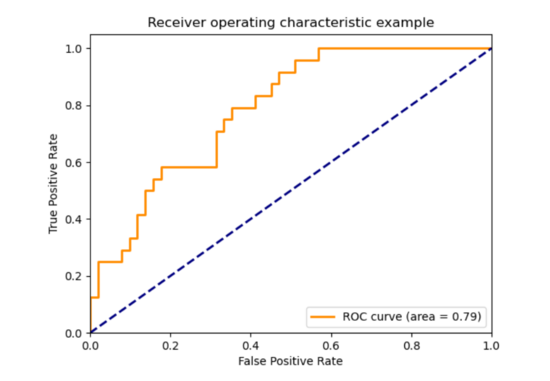
現在，我們如何繪制ROC？

為了回答這個問題，讓我帶您回到上面的表1。僅考慮M1模型。您會看到，對于所有x值，我們都有一個概率得分。在該表中，我們將得分大于0.5的數據點分配為類別1。現在，以概率分數的降序對所有值進行排序，并以等于所有概率分數的閾值一一取值。然后，我們將獲得閾值= [0.96,0.94,0.92,0.14,0.11,0.08]。對應于每個閾值，預測類別，并計算TPR和FPR。您將獲得6對TPR和FPR。只需繪制它們，您將獲得ROC曲線。

注意：由于最大TPR和FPR值為1，因此ROC曲線下的面積（AUC）在0和1之間。

藍色虛線下方的區域是0.5。AUC = 0表示模型很差，AUC = 1表示模型完美。只要您模型的AUC分數大于0.5。您的模型很有意義，因為即使是隨機模型也可以得分0.5 AUC。

非常重要：   即使是從不平衡的數據集生成的啞模型，您也可以獲得很高的AUC。因此，在處理不平衡的數據集時請務必小心。

注意：   只要維持順序，AUC與數值概率分數無關。只要所有模型在根據概率得分排序后給出相同順序的數據點，所有模型的AUC都將相同。

對數損失

該性能度量檢查數據點的概率得分與截止得分的偏差，并分配與偏差成比例的懲罰。

對于二進制分類中的每個數據點，我們使用以下公式計算對數損失：

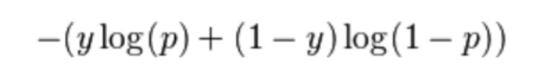
其中p =數據點屬于類別1的概率，y是類別標簽（0或1）。

假設某些x_1的p_1為0.95，某些x_2的p_2為0.55，并且符合1類條件的截止概率為0.5。然后兩者都符合類別1的條件，但是p_2的對數損失將比p_1的對數損失大得多。

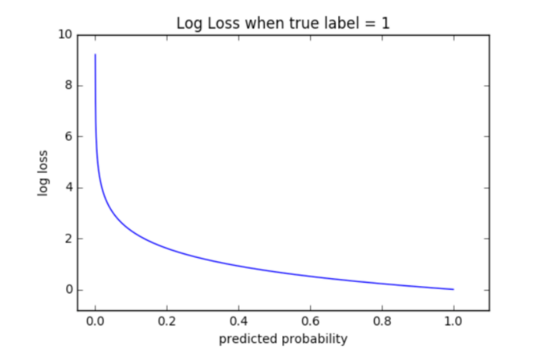
從曲線中可以看到，對數損失的范圍是[0，無窮大]。

對于多類別分類中的每個數據點，我們使用以下公式計算對數損失：

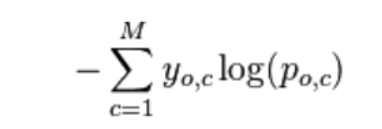
如果x（o，c）屬于類別1，則y（o，c）=1。其余概念相同。

測定系數

用 R 2 表示   。 在預測測試集的目標值時，我們會遇到一些誤差（e_i），這是預測值與實際值之間的差。

假設我們有一個包含n個條目的測試集。眾所周知，所有數據點都有一個目標值，例如[y1，y2，y3…….yn]。讓我們將測試數據的預測值設為[f1，f2，f3，……fn]。

通過使用以下公式計算   殘差平方 和，即所有誤差（e_i）平方的總和，   其中fi是第i個數據點的模型的預測目標值。

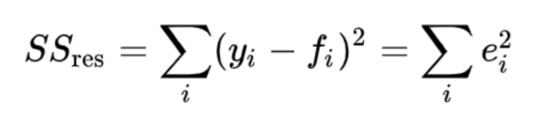
取所有實際目標值的平均值：

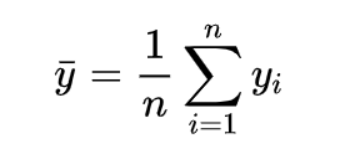
然后計算與測試集目標值的方差成正比的   總平方和 ：

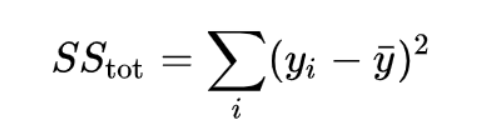
如果同時觀察兩個平方和的公式，則可以看到唯一的區別是第二項，即y_bar和fi。平方總和在某種程度上給我們一種直覺，即它僅與殘差平方和相同，但預測值為[ȳ，ȳ，ȳ，…….ȳ，n次]。是的，您的直覺是正確的。假設有一個非常簡單的均值模型，無論輸入數據如何，均能每次預測目標值的平均值。

現在我們將R²表示為：

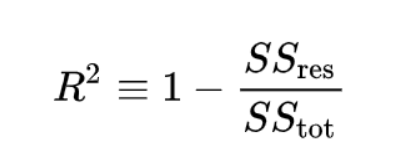
正如您現在所看到的，R²是一種度量，用于將模型與非常簡單的均值模型進行比較，該均值模型每次均返回目標值的平均值，而與輸入數據無關。比較有4種情況：

情況1：SS_R = 0

（R²= 1）完美的模型，完全沒有錯誤。

情況2：SS_R> SS_T

（R²<0）模型甚至比簡單的均值模型差。

情況3：SS_R = SS_T

（R²= 0）模型與簡單均值模型相同。

情況4：SS_R <SS_T

（0 <R²<1）模型還可以。

摘要

因此，簡而言之，您應該非常了解您的數據集和問題，然后您始終可以創建一個混淆矩陣，并檢查其準確性，精度，召回率，并繪制ROC曲線，并根據需要找出AUC。但是，如果您的數據集不平衡，請不要使用準確性作為度量。如果您想對模型進行更深入的評估，以使概率分數也得到權重，請選擇對數損失。

請記住，請務必評估您的訓練！