最強總結,機器學習必會的評估指標
今天給大家分享機器學習中常用的評估指標。

機器學習的評估指標是用于衡量模型在特定任務中的性能,幫助我們判斷模型是否在測試集上有效,并指導模型的優(yōu)化和調整。
評估指標因任務的不同而有所區(qū)別,常見的任務包括分類、回歸等。
分類問題評估指標
分類問題是指將輸入樣本分類為某個離散標簽的任務。
常見的評估指標有以下幾種。
1.混淆矩陣
顧名思義,混淆矩陣給出一個 N*N 矩陣作為輸出,其中 N 是目標類的數量。
混淆矩陣是分類器做出的正確和錯誤預測數量的表格總結。
該矩陣將實際值與機器學習模型的預測值進行比較。
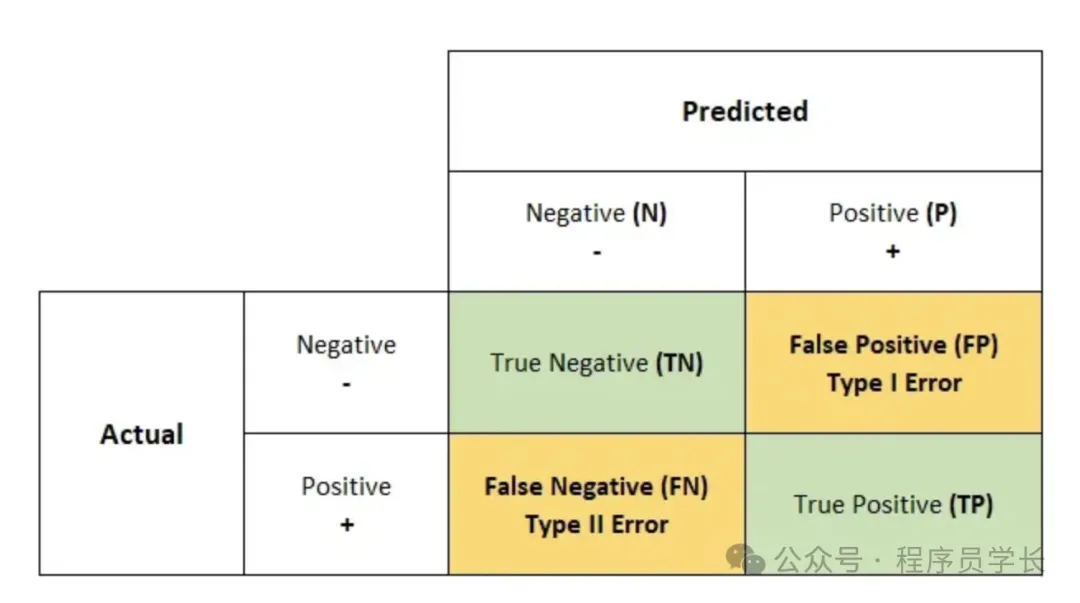
- 真正例(True Positive, TP):模型正確預測為正例的數量。
- 假正例(False Positive, FP):模型錯誤預測為正例的數量。
- 真負例(True Negative, TN):模型正確預測為負例的數量。
- 假負例(False Negative, FN):模型錯誤預測為負例的數量。
2.準確率 (Accuracy)
準確率是指模型預測正確的樣本數占總樣本數的比例。
公式
適用場景
當各類別樣本數量較為均衡時,準確率是一個好的評估指標。
from sklearn.metrics import accuracy_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
accuracy = accuracy_score(y_true, y_pred)
print("Accuracy:", accuracy)3.精確率 (Precision)
精確率是指被模型預測為正類的樣本中,真正為正類的比例。
公式
適用場景
當誤將負類預測為正類的代價較高時(如垃圾郵件分類)。
from sklearn.metrics import precision_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
precision = precision_score(y_true, y_pred)
print("Precision:", precision)4.召回率 (Recall)
召回率是指正類樣本中被模型正確預測為正類的比例。
公式
適用場景
當誤將正類預測為負類的代價較高時(如疾病檢測)。
from sklearn.metrics import recall_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
recall = recall_score(y_true, y_pred)
print("Recall:", recall)5.特異性
特異性是分類模型對負類樣本的識別能力的度量,它表示所有真實為負類的樣本中,模型正確識別為負類的比例。
公式
from sklearn.metrics import confusion_matrix
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
specificity = tn / (tn + fp)
print("Specificity:", specificity)6.F1-Score
F1-Score 是精確率和召回率的調和平均,用于平衡兩者之間的影響。
適用場景
當需要在精確率和召回率之間找到平衡點時,使用 F1-Score。
from sklearn.metrics import f1_score
y_true = [0, 1, 0, 1]
y_pred = [0, 0, 0, 1]
f1 = f1_score(y_true, y_pred)
print("F1 Score:", f1)7.AUC-ROC
AUC (Area Under the Curve) 表示 ROC 曲線下的面積,AUC 越高,模型越好。下圖顯示了 ROC 曲線,y 軸為 TPR(真陽性率),x 軸為 FPR(假陽性率)。

回歸問題評估指標
回歸問題的目標是預測連續(xù)值,常見的評估指標有以下幾種。
1.均方誤差 (MSE)
MSE 是預測值與真實值之間差異的平方的平均值,常用于衡量模型的預測誤差。
適用場景
對大誤差比較敏感的場景,因為誤差平方放大了大的偏差。
from sklearn.metrics import mean_squared_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
print("Mean Squared Error (MSE):", mse)2. 均方根誤差 (RMSE)
RMSE是 MSE 的平方根,用于衡量預測誤差的平均幅度。
RMSE 的單位與原始預測變量相同,因此便于理解。
from sklearn.metrics import mean_squared_error
import numpy as np
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mse = mean_squared_error(y_true, y_pred)
rmse = np.sqrt(mse)
print("Root Mean Squared Error (RMSE):", rmse)3. 平均絕對誤差 (MAE)
MAE 是預測值與真實值之間差異的絕對值的平均值,衡量模型預測誤差的平均大小。
適用場景
對所有誤差同等看待的場景。
from sklearn.metrics import mean_absolute_error
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
mae = mean_absolute_error(y_true, y_pred)
print("Mean Absolute Error (MAE):", mae)4. R方值
R2 表示模型解釋了目標變量總變異的比例,取值范圍為 0到1,數值越大表示模型越好。
適用場景
適用于評估回歸模型的整體性能。
from sklearn.metrics import r2_score
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2 = r2_score(y_true, y_pred)
print("R-squared (R^2):", r2)5.調整后的 R2
調整后的 是在 的基礎上引入了對模型復雜度的懲罰,考慮了模型中自變量的數量。
其公式為
其中:
- n 是樣本數量。
- p 是模型中的自變量(特征)數量。
from sklearn.metrics import r2_score
def adjusted_r2(r2, n, k):
return 1 - (1 - r2) * (n - 1) / (n - k - 1)
y_true = [3, -0.5, 2, 7]
y_pred = [2.5, 0.0, 2, 8]
r2 = r2_score(y_true, y_pred)
n = len(y_true) # Number of observations
k = 1 # Number of predictors
adj_r2 = adjusted_r2(r2, n, k)
print("Adjusted R-squared:", adj_r2)






































