作為一種有趣的棋盤游戲，數(shù)獨誕生100周年之后，它是如何成為計算研究的焦點之一的呢?探索如何使用人工智能或量子計算機從頭開始創(chuàng)建一個智能數(shù)獨求解器。

在深入探究之前，先來了解一下歷史

馬克•布洛赫說:"歷史被稱為學科之母。"那么，讓我們來談談著名的數(shù)獨游戲是如何誕生的吧。這個故事可以追溯到19世紀末，起源于法國。法國日報《世紀報》(Le Siecle)發(fā)布了一款9x9大小的猜謎游戲，它需要算術運算而不是邏輯運算，它的數(shù)字是兩位數(shù)，而不是1- 9。它的游戲性質與數(shù)獨游戲(Sudoku)類似，即把橫排、列和對角線的數(shù)字相加，也會得到相同的數(shù)字。1979年，退休的建筑師和puzzler Howard Garns被認為是現(xiàn)代數(shù)獨游戲的創(chuàng)造者，該游戲以數(shù)字地名的名義首次在戴爾雜志上發(fā)表。1986年，日本一家名為Nikoli的拼圖公司首次以Sudoku的名字出版了這個拼圖。

在解決數(shù)獨游戲的問題框架

數(shù)獨是一個約束滿足問題(CSP)的真實例子，因為變量集、域集和約束集都是有限的。我們必須在一個9x9表中輸入1-9之間的數(shù)字，這樣每一行、每列和每3x3子表中的數(shù)字都只包含一個數(shù)字。 Sudoku也存在另一種變化，即Diagonal Sudoku，它在表對角線的每個對角線中都規(guī)定了一組額外的約束，每個數(shù)字必須準確地具有一次特征。 我們知道約束滿足域，最優(yōu)解必須滿足所有約束，或更具體地說，它應該遵守游戲規(guī)則。 最優(yōu)解將滿足集合中的所有約束，從而解決難題。

計算上，可以用非確定性多項式時間(NP)解決求解數(shù)獨的約束，因為可以使用一些非常特殊的蠻力算法來解決約束，并且也可以在多項式時間內測試解集的有效性，其中輸入 該問題與多項式長度的一組解有關。 完全解決的數(shù)獨就是拉丁方格的示例(如Euler所述，n x n數(shù)組填充有n個不同的符號)。 數(shù)獨問題可以認為是圖形著色問題，其中我們僅需要使用9種顏色對圖形進行著色，而裸露的字母可以認為是部分顏色。

使用人工智能算法集滿足約束

計算科學的基本原理是依靠邏輯來滿足某些約束的能力。 在解決數(shù)獨問題時，我們必須訓練求解器以尋找除基本規(guī)則外的一些特定的獲勝模式。 因此，問題在于系統(tǒng)不僅在盲目地遵循規(guī)則，而且在考慮其近期和長期影響的同時做出一些決策。 這些模式稱為啟發(fā)式。 類似于巧遇游戲知識和技巧的專家玩家，僅了解基本規(guī)則并不能使他們成為游戲專家。 因此，當我們開發(fā)算法并解決問題時，我們必須牢記有用的啟發(fā)式方法，我們還應將其包含在程序中，以使其在獲勝時變得更聰明，更有用。

對于我們的Sudoku Solver，我們將輸入81個數(shù)字的序列作為字符串，并用'。'(句號)表示未解決的數(shù)字。 為了解決該問題，我們將"。"替換為可以放入該單元格的所有可能數(shù)字。

根據(jù)數(shù)獨的限制，我們不能在任何單元格附近的行，列或3x3子正方形中多次使用一個數(shù)字。 在對角數(shù)獨的情況下，我們還必須考慮相同的約束。 我們首先用所有可能的數(shù)字1到9替換句點。我們使用以下grid_values函數(shù)以編程方式進行此操作。

# For the sake of caluclation we take rows as alphaneumeric and columns as numeric.  
rows = 'ABCDEFGHI'  
columns = '123456789' 
boxes = [r + c for r in rows for c in columns]  #every possible cell combination in the grid. 
def grid_values(grid):  """ 
  Take in the Unsolved Sudoku Sequence and replaces the unsolved boxes initially with all 
  possible values which can get into that cell. Lastly returns a dictionary containing the  
  values at all cell positions along with cells.  
  """ 
  values = []  every_digits = '123456789' 
  for n in grid: 
    if c == '.':   # replacing every unsolved value with every possible value initially. 
      values.append(every_digits)    else:          # if already solved, causing it no change.  
      values.append(c)   assert len(values) == 81 
   return dict(zip(boxes, values)) #returning the sudoku grid with all possible cell values.  

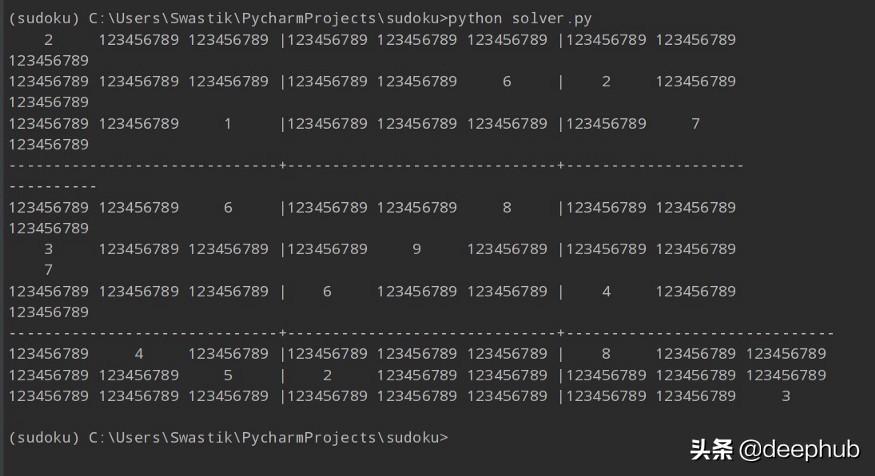
首先在所有未解決的單元格中分配所有可能的值。

現(xiàn)在，我們用1到9之間的所有可能數(shù)字替換了未解決的單元格，從數(shù)獨的基本規(guī)則中我們知道，如果數(shù)字已經(jīng)在該行，列和3x3子字段中使用過，我們就不能使用它兩次。 因此，讓我們消除它們，如果我們在未解決的網(wǎng)格中遇到它們時，我們最初已經(jīng)用所有可能的數(shù)字填充了它們。 因此，讓我們看一下如何使用消除python方法從未解決的單元中消除那些不相關的數(shù)字。

columns_reversed = columns[::-1] #reversing the columns for calculating the Diagonal Units. 
def make_combinations(m, n):  """ 
  Takes in input of generally iterables and creates all possible combintation out of them. 
  args: 
   a: string iterable 
   b: string iterable 
   return : list of all possible combination.  
  """ 
  return [x + y for x in m for y in n] 
row_units = [make_combinations(r, columns) for r in rows] 
column_units = [make_combinations(rows, c) for c in columns] 
sub_square_units = [make_combinations(m, n) for m in ('ABC', 'DEF', 'GHI')  
                    for n in ('123','456','789')] 
diagonal_1_units = [[rows[i]+columns[i] for i in range(len(rows))]] 
diagonal_2_units = [[rows[i]+columns_reversed[i] for i in range(len(rows))]] 
diagonal_units = diagonal_1_units + diagonal_2_unitsall_units = row_units + column_units + square_units + diagonal_unitsunits = dict((b, [u for u in all_units if b in u]) for b in boxes) 
peers = dict((b, set(sum(units[b], [])) - {b}) for b in boxes) 
def eliminate(values):  """ 
  Eliminate the redundant numbers from the unsolved cells if the number already appeared once  
  in the peer of the current cell.  
  What we do here is we erase that redundant number from the unsolved value cells if appeared once.  
  """ 
  solved_cells = [box for box in values.keys() if len(values[box]) == 1] # cell is solved if there's only one digit 
  for box in solved_cells: 
    value_at_cell = values[box]   # retrieve the current value at that cell. 
    for peer in peers[box]:       # check for the cell's peers if the value appears again. 
      values[peer] = values[peer].replace(value_at_cell, '') 
   return values   # return the modified values dictionary. 

因此，在滿足這些約束的同時，有時我們會遇到一些只能放置一個數(shù)字的單元格，但除該數(shù)字外，其他數(shù)字對于該特定單元格都不再可行。 我們首先要填寫這些內容。 有了適當?shù)慕鉀Q方案。 我們稱此為"唯一選擇"，它是解決數(shù)獨網(wǎng)格單元的最簡單的啟發(fā)式方法。

def only_choice(values): 
  """ 
  If in order to satisfy the constraints of the Sudoku Puzzle there is only a single viable option 
  we fill in the Cell with that option only and thereby obtain a solve for the cell.  
   
  """ 
  for unit in all_units:     #searching across all the vicinity of the cell. 
    for digit in '123456789':   
      to_be_filled = [cell for cell in unit if unit in values[unit]] 
      if len(to_be_filled) == 1:  # if there exists only a single cell in the unit which is not solved 
        values[to_be_filled[0]] = digit  # We fill in the cell with its proper answer.     
  return values 

在迄今為止圍繞約束滿足的過程中，可能會出現(xiàn)以下情況：一個單元中將有兩個未解決的像元(考慮行，列和3x3子正方形)，其中只能分配兩個特定的剩余數(shù)。 因此，這兩個數(shù)字可以有效地從同一單元中其他單元格上的可能數(shù)字中刪除。 這種啟發(fā)式方法稱為裸雙胞胎。 該算法的實現(xiàn)專門制作了網(wǎng)格值的深層副本，并檢查了裸胎雙胞胎的可行性，即是否存在兩個僅能接受兩個特定值的未解決像元，如果可行，它將繼續(xù)進行并從其他兩個值中刪除這兩個值 同一單元中的單元格。 我們使用如下所示的nude_twins函數(shù)以編程方式實現(xiàn)它：

def naked_twins(values): 
    """ 
    If there are two unsolved cells in a same unit exist such that it can only be filled by only  
    two specific digits, then those two digits can be safely removed from all other cells in the same unit. 
    """ 
    twins_possible = [unit for unit in values.keys() if len(values[unit]) == 2]   
    twins = [[unit1, unit2] for unit1 in twins_possible for unit2 in peers[unit1]  
                     if set(values[unit1]) == (set(values[unit2]))]    #confimed Naked Twins 
    for twin in twins: 
        unit1 = twin[0]  
        unit2 = twin[2] 
        peers1 = set(peers[unit1])   
        peers2 = set(peers[unit2]) 
        common_peers = peers1 & peers2  #finding the intersection between the peers of the two naked twin element 
        for peer in common_peers: 
            if len(values[peer]) >  1: 
                for value in values[unit1]: 
                    values[peer] = values[peer].replace(val, ''))  # Erasing the values.  
    return values 

現(xiàn)在，我們嘗試通過重復應用這三個約束滿足算法并檢查它是否卡住并且無法進一步減少，來盡可能地減少難題。 我們通過使用reduce_puzzle函數(shù)以編程方式執(zhí)行此操作。 我們要做的是在for循環(huán)中調用前三個函數(shù)，并在網(wǎng)格值的輸入和輸出序列中的已解決單元數(shù)相同時終止該函數(shù)，這意味著不能再進一步減小它 僅約束滿足算法。

def reduce_puzzle(values): 
    """ 
    Applying the 4 Constraint Satisfaction Algorithms until it is not further reducible.  
    Checking if the Number of Solved Cells between the iteration. 
    """ 
    solved_values = [unit for unit in values.keys() if len(values[unit]) == 1] # considering solved cells 
    stuck = False #boolean flag to determine the end of loop 
    while not stuck: 
        prev_solved_values = len([unit for unit in values.keys() if len(values[unit]) == 1]) #checkpoint 1 
        values = eliminate(values) # applying Elimination CSP 
        values = only_choice(values) # applying Only Choice CSP 
        values = naked_twins(values)  # applying Naked Twins CSP 
        after_solved_values = len([unit for unit in values.keys() if len(values[unit]) == 1]) 
        stuck = after_solved_values == prev_solved_values  # Getting out of loop is the number of solved cell is still the same as the previous iteration. 
         
        if len([unit for unit in values.keys() if len(values[unit]) == 0]): 
            return False   # if there's problems in the internal representation of the sudoku grid return False.  
    return values           # return the reduced grid values.    

如果數(shù)獨網(wǎng)格仍未通過約束滿足問題解決，則部分解決方案將到達輸出，其中一些單元格仍將分配給某些可能的值。 在這種情況下，我們要做的是使用搜索樹搜索那些位置中的最佳數(shù)字集。 我們使用深度優(yōu)先搜索(DFS)算法遍歷搜索樹。 因此，基本上，使用DFS，我們用相同的網(wǎng)格創(chuàng)建了幾個實例，并為每個尚未解決的單元嘗試了不同的可能分配。 我們遞歸地要求CSP算法根據(jù)搜索結果減少網(wǎng)格。 我們以編程方式實現(xiàn)它，如下所示：

def search(values): 
    """ 
    Recursive Depth-First Search: If the sudoku grid is not further reducible by constraint satisfaction 
    a few of the cells will be left with different options and with DFS with search for the optimal  
    values for those yet-unsolved cells.   
    """ 
    values = reduce_puzzle(values) # We call the Reduction Function to reduce the puzzle further based on the search results across iterations.  
    if values is False: 
        return False 
    if all(len(values[b]) == 1 for b in boxes): 
        print("Sudoku Problem Solved!") 
        return values 
    m, n = min((len(values[b]), b) for b in boxes if len(values[b]) > 1) 
    for value in values[n]: 
        new_sudoku = values.copy() 
        new_sudoku[n] = value 
        attempted = search(new_sudoku) 
        if attempted: 
            return attempted     

我們使用display sudoku函數(shù)將輸入的字符串序列顯示為二維9x9 Sudoku網(wǎng)格：

def display(values): 
    """ 
    Display the values as a 2-D grid. 
    Input: The sudoku in dictionary form 
    """ 
    width = 1 + max(len(values[b]) for b in boxes) 
    line = '+'.join(['-' * (width * 3)] * 3) 
    for r in rows: 
        print(''.join(values[r + c].center(width) + ('|' if c in '36' else '') 
                      for c in cols)) 
        if r in 'CF': 
            print(line)    return 

為了解決數(shù)獨序列，我們將上述函數(shù)調用如下：

if __name__ == "__main__": 
    diag_sudoku_grid = '2.............62....1....7...6..8...3...9...7...6..4...4....8....52.............3' 
    values = grid_values(diag_sudoku_grid) 
    values = reduce_puzzle(values) 
    values = search(values) 
    display(values) 

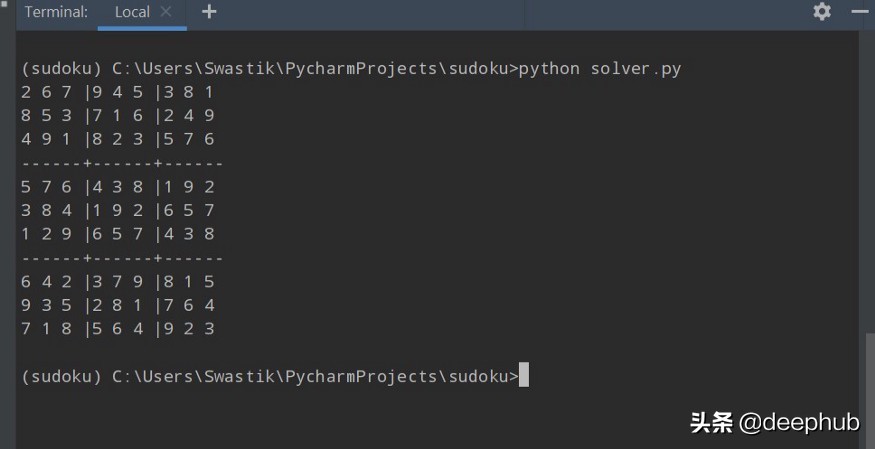
輸出如下所示，其中一組算法已成功計算出答案。

解決數(shù)獨作為約束滿足問題的量子方法

現(xiàn)在，我們將嘗試使用"量子模擬退火"解決簡單的Sudoku網(wǎng)格。 首先，什么是模擬退火? 對于這樣的優(yōu)化問題，我們的想法是使用一些次優(yōu)啟發(fā)式算法，并獲得最優(yōu)的啟發(fā)式算法集以獲得最優(yōu)解。 我們在這里使用DWave AQC模型(糖尿病量子計算)來采樣滿足前面討論的約束的最佳解決方案。...

使用DWave Kerberos混合采樣器：

在本示例中，我們正在使用DWave隨附的混合求解器。 它通過運行并行搜索來找出最佳的啟發(fā)式方法。 它是一種混合求解器，因為它同時使用了量子計算和經(jīng)典的計算特性。 它也是一個分解采樣器，在處理時使用異步工作流。 它包含在DWave Systems的Ocean SDK軟件包中。 要開始本地開發(fā)，請確保您的系統(tǒng)上安裝了Python 3.5+，然后發(fā)出以下命令。

python -m pip install --upgrade pip 
pip install dwave-ocean-sdk 

使用二進制二次模型(BQM)進行計算

我們無法構造直接準備將其饋送到Quantum Computers的約束，我們需要一個中間表示來將其饋入。 這就是為什么我們將使用BQM的原因，幸運的是，DWave Ocean SDK已經(jīng)提供了一種稱為"組合"的工具，可用于將約束滿足問題歸結為BQM。 首先，顧名思義，二進制二次模型本身就是一個方程系統(tǒng)，它是二次的，用二進制表示。 由于計算的復雜性更高，Quantum計算機使用這些計算可以大大加快開發(fā)過程。 因此，在游戲中，我們決定使用dimod的組合工具，該工具將返回一個二進制二次模型，該模型對于其輸入變量和內部變量的k個組合中的每一個均最小。

我們首先從dwave-ocean-sdk導入必要的軟件包，并在實際讀入Sudoku Grid之前進行一些完整性檢查。

import dimod   
import math  
import sys 
import dimod.generators.constraints import combinations 
from hybrid.reference import KerberosSampler 
def prettify(row, col, digit):    return "{row}, {col}_{digit}".format(row, col, digit) 
def read_matrix(filename):    with open(filename, 'r') as f: 
        all_lines = f.read()    lines = []    for line in all_lines: 
        new_line = line.rstrip()        if new_line: 
            new_line = list(map(int, new_line.split(' '))) 
            lines.append(new_line) 
    return lines  
def sanity_check(matrix):    n = len(matrix) 
    m = int(math.sqrt(n)) 
    unique_digits = set(range(1, 1+n)) 
    for row in matrix: 
        if set(row) != unique_digits: 
            print("Error in row", row) 
            return false 
    for j in range(n): 
        col = [matrix[i][j] for i in range(n)] 
        if set(col) != unique_digits: 
            print("Error in column", col) 
    subsquare_idx = [(i, j) for i in range(m) for j in range(m)] 
    for r_scalar in range(m): 
        for c_scalar in range(m): 
            subsquare = [matrix[i + r_scalar * m ][j + c_scalar * m] for i, j in subsquare_idx] 
            if set(subsquare) != unique_digits: 
                print('Error in sub-square', subsquare) 
                return True 
    return True 

現(xiàn)在，我們使用Sudoku Grid的行，列和子正方形索引的所有可用變量組合，使用組合工具來創(chuàng)建二進制二次模型。

def main(): 
    if len(sys.argv) > 1: 
        filename = sys.argv[1] 
            matrix = read_matrix(filename)    n = len(matrix) 
    m = int(math.sqrt(n)) 
    digits = range(1, n+1) 
    bqm = dimod.BinaryQuadraticModel({}, {}, 0.0, dimod.SPIN) 
    for row in range(n): 
        for col in range(n): 
            node_digits = [prettify(row, col, digit) for digit in digits] 
            one_digit_bqm = combinations(node_digits, 1) 
            bqm.update(one_digit_bqm)    for row in range(n): 
        for digit in digits: 
            row_nodes = [prettify(row, col, digit) for col in range(n)] 
            row_bqm = combinations(row_nodes, 1) 
            bqm.update(row_bqm)    for col in range(n): 
        for digit in digits: 
            col_nodes = [prettify(row, col, digit) for row in range(n)] 
            col_bqm = combinations(col_nodes, 1) 
            bqm.update(col_bqm)if __name__ == "__main__": 
    main() 

就是這樣。 我們已經(jīng)成功實現(xiàn)了兩種智能解決方案，其中一種使用經(jīng)典計算，并且使用了功能非常強大的人工智能啟發(fā)式算法，甚至可以解決對角數(shù)獨網(wǎng)格。 第二種方法使用異步混合啟發(fā)式采樣器，該采樣器也恰好使用絕熱量子計算模型的模擬退火來將約束滿足問題轉換為二進制二次模型以對其進行采樣，從而獲得最佳采樣解。