[[345646]]

前一段時間，我們介紹了LeetCode上面的一個經典算法題【兩數之和問題】。

這一次，我們把問題做一下擴展，嘗試在數組中找到和為“特定值”的三個數。

題目的具體要求是什么呢?給定下面這樣一個整型數組：

 

我們隨意選擇一個特定值，比如13，要求找出三數之和等于13的全部組合。

由于5+6+2=13， 5+1+7=13，3+9+1=13，所以最終的輸出結果如下：

【5， 6，2】

【5， 1，7】

【3， 9，1】

 

小灰的思路，是把原本的“三數之和問題”，轉化成求n次“兩數之和問題”。

 

我們以上面這個數組為例，選擇特定值13，演示一下小灰的具體思路：

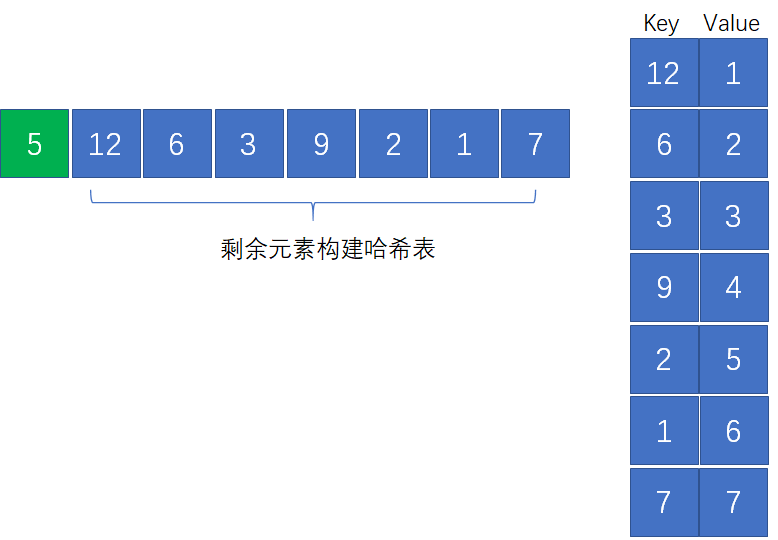
第1輪，訪問數組的第1個元素5，把問題轉化成從后面元素中找出和為8(13-5)的兩個數：

 

如何找出和為8的兩個數呢?按照上一次所講的，我們可以使用哈希表高效求解：

 

第2輪，訪問數組的第2個元素12，把問題轉化成從后面元素中找出和為1(13-12)的兩個數：

 

第3輪，訪問數組的第3個元素6，把問題轉化成從后面元素中找出和為7(13-6)的兩個數：

 

以此類推，一直遍歷完整個數組，相當于求解了n次兩數之和問題。

 

 

public static List<List<Integer>> threeSum(int[] nums, int target) { 
       List<List<Integer>> resultList = new ArrayList<>(); 
       for (int i = 0; i < nums.length; i++) { 
           Map<Integer, Integer> map = new HashMap<>(); 
           int d1 = target - nums[i]; 
           //尋找兩數之和等于d1的組合 
           for (int j = i+1; j < nums.length; j++) { 
               int d2 = d1 - nums[j]; 
               if (map.containsKey(d2)) { 
                   resultList.add(Arrays.asList(nums[i], d2, nums[j])); 
               } 
               map.put(nums[j], j); 
           } 
       } 
       return resultList; 
   } 

在上面的代碼中，每一輪解決“兩數之和問題”的時間復雜度是O(n)，一共迭代n輪，所以該解法總的時間復雜度是O(n²)。

至于空間復雜度，同一個哈希表被反復構建，哈希表中最多有n-1個鍵值對，所以該解法的空間復雜度是O(n)。

 

我們仍然以之前的數組為例，對數組進行升序排列：

 

這樣說起來有些抽象，我們來具體演示一下：

第1輪，訪問數組的第1個元素1，把問題轉化成從后面元素中找出和為12(13-1)的兩個數。

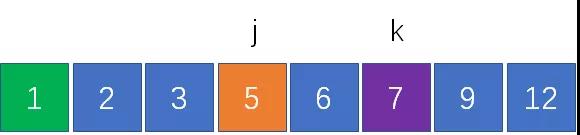
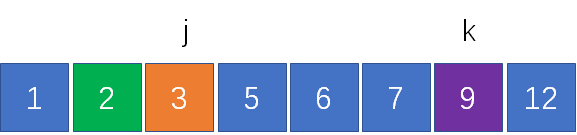
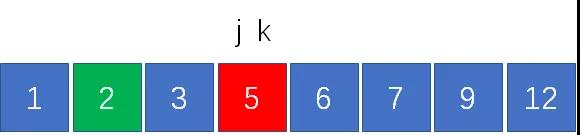
如何找出和為12的兩個數呢?我們設置兩個指針，指針j指向剩余元素中最左側的元素2，指針k指向最右側的元素12：

 

計算兩指針對應元素之和，2+12 = 14 > 12，結果偏大了。

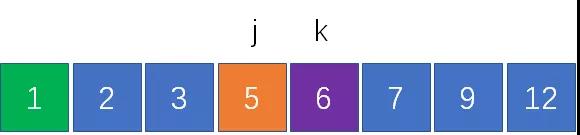
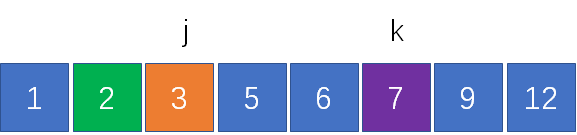
由于數組是按照升序排列，k左側的元素一定小于k，因此我們把指針k左移一位：

 

計算兩指針對應元素之和，2+9 = 11< 12，這次結果又偏小了。

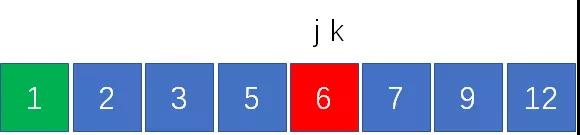
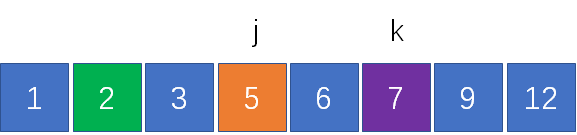
j右側的元素一定大于j，因此我們把指針j右移一位：

 

計算兩指針對應元素之和，3+9 = 12，正好符合要求!

因此我們成功找到了一組匹配的組合：1，3，9

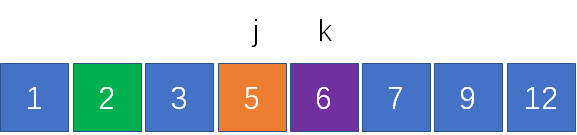
但這并不是結束，我們要繼續尋找其他組合，讓指針k繼續左移：

 

計算兩指針對應元素之和，3+7 = 10< 12，結果偏小了。

于是我們讓指針j右移：

 

計算兩指針對應元素之和，5+7 = 12，又找到符合要求的一組：

1，5，7

我們繼續尋找，讓指針k左移：

 

計算兩指針對應元素之和，5+6 = 11< 12，結果偏小了。

于是我們讓指針j右移：

 

此時雙指針重合在了一起，如果再繼續移動，就有可能和之前找到的組合重復，因此我們直接結束本輪循環。

第2輪，訪問數組的第2個元素2，把問題轉化成從后面元素中找出和為11(13-2)的兩個數。

我們仍然設置兩個指針，指針j指向剩余元素中最左側的元素3，指針k指向最右側的元素12：

 

計算兩指針對應元素之和，3+12 = 15 > 11，結果偏大了。

我們讓指針k左移：

 

計算兩指針對應元素之和，3+9 = 12 > 11，結果仍然偏大。

我們讓指針k繼續左移：

 

計算兩指針對應元素之和，3+7 = 10 < 11，結果偏小了。

我們讓指針j右移：

 

計算兩指針對應元素之和，5+7 = 12 > 11，結果又偏大了。

我們讓指針k左移：

 

計算兩指針對應元素之和，5+6 = 11，于是我們又找到符合要求的一組：

2，5，6

我們繼續尋找，讓指針k左移：

 

此時雙指針又一次重合在一起，我們結束本輪循環。

按照這個思路，我們一直遍歷完整個數組。

像這樣利用兩個指針指向數組兩端，不斷向中間靠攏調整來尋找匹配組合的方法，就是雙指針法，也被稱為“夾逼法”。

 

 

public static List<List<Integer>> threeSumv2(int[] nums, int target) { 
    Arrays.sort(nums); 
    List<List<Integer>> resultList = new ArrayList<List<Integer>>(); 
    //大循環 
    for (int i = 0; i < nums.length; i++) { 
        int d = target - nums[i]; 
        // j和k雙指針循環定位，j在左端，k在右端 
        for (int j=i+1,k=nums.length-1; j<nums.length; j++) { 
            // k指針向左移動 
            while (j<k && (nums[j]+nums[k])>d) { 
                k--; 
            } 
            //雙指針重合，跳出本次循環 
            if (j == k) { 
                break; 
            } 
            if (nums[j] + nums[k] == d) { 
                List<Integer> list = Arrays.asList(nums[i], nums[j], nums[k]); 
                resultList.add(list); 
            } 
        } 
    } 
    return resultList; 
} 

上面這段代碼表面上有三層循環，但每一輪指針j和k的移動次數加起來最多n-1次，因此該解法的整體時間復雜度是O(n²)。

最關鍵的是，該解法并沒有使用額外的集合(排序是直接在輸入數組上進行的)，所以空間復雜度只有O(1)!

本文轉載自微信公眾號「程序員小灰」，可以通過以下二維碼關注。轉載本文請聯系程序員小灰公眾號。