[[376536]]

本文轉載自微信公眾號「程序新視界」，作者丑胖俠二師兄 。轉載本文請聯系程序新視界眾號。  

 前言

一道小學加法題，竟然在LeetCode上被標記為“中等”難度，有些人“流下了沒有技術的眼淚”，有些人“一頓操作猛如虎，一看擊敗百分五……”。今天我們來看看LeetCode的第二道題“兩數相加”。

“兩數相加”

先來看題目描述，對應官方鏈接：https://leetcode-cn.com/problems/add-two-numbers

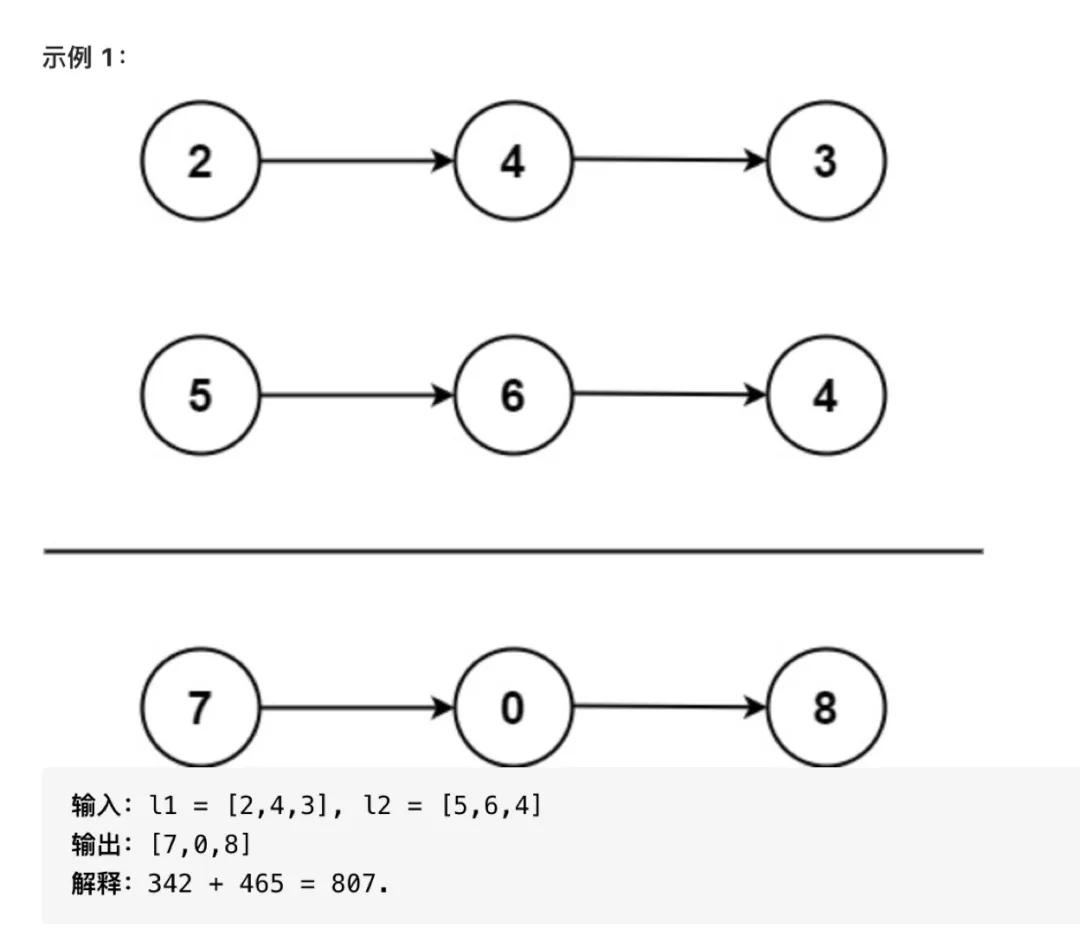
給你兩個非空的鏈表，表示兩個非負的整數。它們每位數字都是按照逆序的方式存儲的，并且每個節點只能存儲一位數字。請你將兩個數相加，并以相同形式返回一個表示和的鏈表。你可以假設除了數字0之外，這兩個數都不會以0開頭。

兩數相加

鏈表節點的數據結構如下：

public class ListNode { 
   int val; 
   ListNode next; 
   ListNode() {} 
   ListNode(int val) { this.val = val; } 
   ListNode(int val, ListNode next) { this.val = val; this.next = next; } 
 } 

題目說明

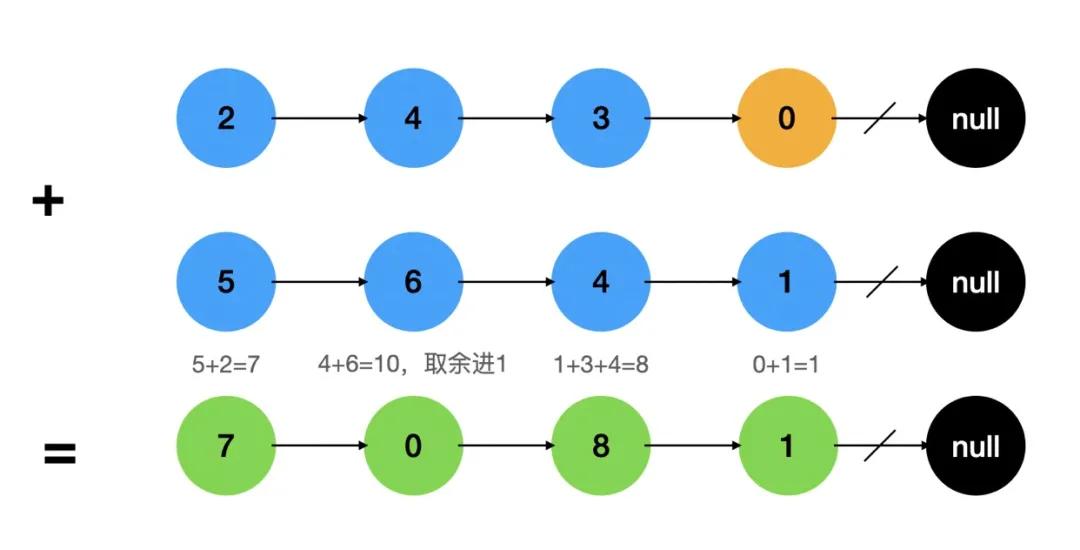
題目描述相對來說比較繞，我們可以直接理解為兩個多位的整數相加，只不過整數的每一位都是通過鏈表進行存儲。比如，整數342，通過鏈表存儲正常來說應該是3->4->2，但是計算時，往往需要從低位開始計算，逢十進一，所以題目中直接將整數表示為2->4->3，這樣反而不用將鏈表順序進行反轉了，直接相加就可以了。

兩數相加

需要注意的是如果兩個鏈表的長度不同，則可以認為長度短的鏈表的后面有若干個 0 ，鏈表遍歷結束，則如果進位值大于0，則還需要在結果鏈表中附加一個值為1的節點。

方法一：模擬

上面已經提到，鏈表是逆序的，因此直接對應數字相加即可。基本操作遍歷兩個列表，逐位計算它們的和，并與當前位置的進位值相加。

比如，兩個鏈表對應位的數字分別為n1和n2，進位為carry(通常為0和1)，則它們的和為(n1 + n2 + carry)，對應位上數字變為(n1 + n2 + carry)%10，新的進位為(n1 + n2 + carry)/10。

如果兩個鏈表長度不一樣，長度短的鏈表后續對應位上值均為0即可。如果遍歷結束之后，carray大于0(也就是等于1)，則在結構鏈表后面新增一個節點，

實現代碼如下：

class Solution { 
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) { 
        ListNode head = null, tail = null; 
        int carry = 0; 
        while (l1 != null || l2 != null) { 
            int n1 = l1 != null ? l1.val : 0; 
            int n2 = l2 != null ? l2.val : 0; 
            int sum = n1 + n2 + carry; 
            if (head == null) { 
                head = tail = new ListNode(sum % 10); 
            } else { 
                tail.next = new ListNode(sum % 10); 
                tail = tail.next; 
            } 
            carry = sum / 10; 
            if (l1 != null) { 
                l1 = l1.next; 
            } 
            if (l2 != null) { 
                l2 = l2.next; 
            } 
        } 
        if (carry > 0) { 
            tail.next = new ListNode(carry); 
        } 
        return head; 
    } 
} 

上述方法時間復雜度的計算與鏈表的長度有關，比如兩個鏈表的長度分別為m和n，則遍歷的次數為max(m,n)，也就m和n中取最大值，所以時間復雜度為O(n)。

由于要對鏈表的每一位進行計算存儲，并且最后如果有進位，還要多加一位，因此最長鏈表為max(m,n)+1，所以空間復雜度為O(n);

通過思路分析，寫出上面的代碼還是比較容易的。但這個題目是否可以考慮用遞歸的形式來解決呢?我們來看看方法二。

方法二：遞歸

第一種方法很簡單，按照正常的思維邏輯來就可以了。但評論區有這樣一句話“不用遞歸沒有靈魂。盡管多數時候，遞歸不見得更有效率。”那么我們就來看看用遞歸的形式如何實現。

class Solution { 
    public ListNode addTwoNumbers(ListNode l1, ListNode l2) { 
        return add(l1,l2,0); 
    } 
    public ListNode add(ListNode l1, ListNode l2, int carry){ 
        if(l1 == null && l2 == null && carry == 0) return null; 
        int x = l1==null ? 0 : l1.val; 
        int y = l2==null ? 0 : l2.val; 
        int sum = x + y + carry; 
        ListNode n = new ListNode(sum % 10); 
        n.next = add(l1==null ? null : l1.next, 
                     l2==null ? null : l2.next, 
                     sum/10); 
        return n;  
    } 
} 

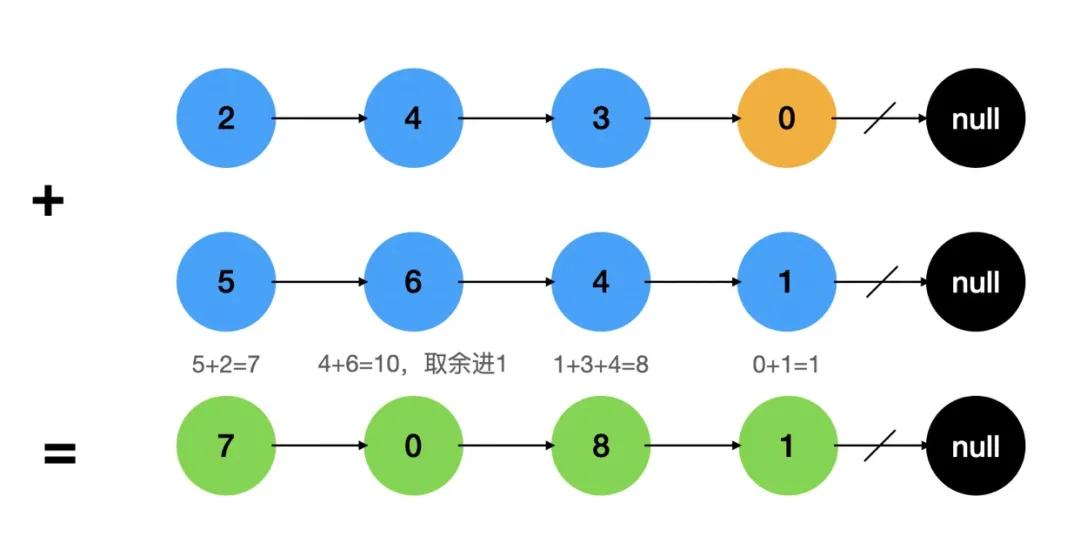
上述代碼的基本迭代邏輯循環如下：

兩數相加

通過上圖我們可以推演一下遞歸調用的時間復雜度。針對遞歸調用的時間復雜度計算，本質上要看：遞歸的次數??每次遞歸中的操作次數。那么，上述方法遞歸了幾次呢?遞歸的次數也是與兩個鏈表最長的那個的長度有關，最后可能會因為進位多算一次，因此遞歸次數為n或n+1，而內部計算并不隨n的變化而變化，執行次數為常數。因此整體時間復雜度為n*1 = O(n)。

空間復雜度依舊與結果鏈表的長度有關，因此依舊為O(n)。

小結

就算法本身而言是比較簡單的，理清思路，逐漸添加判斷即可獲得解法。重點在于大家是否能夠想到通過遞歸算法來進行解答。本道題遞歸算法并沒有讓時間復雜度降低，而在某些情況下通過遞歸算法能將時間復雜度從O(n)降低到O(logn)，這將是很大性能提升。比如，求x的n次方，大家可以嘗試一下。