[[377395]]

前言

今天繼續算法題：從尾到頭打印鏈表

鏈表

在看今天題目之前，我們先了解下鏈表。

鏈表是一種物理存儲單元上非連續、非順序的存儲結構。由于不必須按順序存儲，鏈表的插入和刪除操作可以達到O(1)的復雜度

熟悉數組的都知道，數組是需要一塊連續的內存空間來存儲。而鏈表就不需要，它是通過指針來將內存塊串聯起來。

常見的鏈表結構有：單鏈表、雙向鏈表和循環鏈表。(圖片來自參考鏈接)

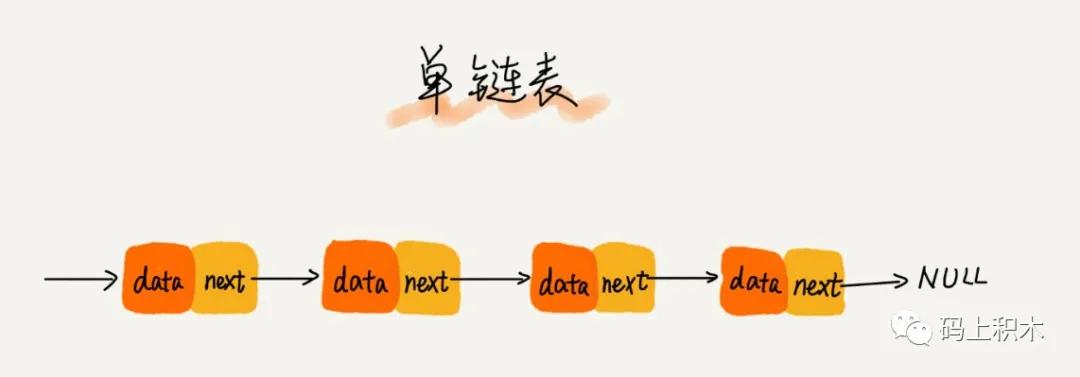
單鏈表

 

第一個接點為頭結點，最后一個結點是尾結點。

從圖中可以看出來：當某個結點不是指向下一個結點，而是指向了null，空地址，那么這個結點就是這個鏈表最后一個結點，也就是尾結點。

當我們插入或者刪除結點只需要修改next結點就行，也就是修改next指針指向地址，比如這樣一個鏈表：

a->next=b, b->next=c, c->next=d 

a下一個結點是b，b下一個結點是c...

如果我們要在ab直接插入一個結點p，得益于鏈表的不連續性，我們只需要修改a的next為p，p的next為b就行了。

a->next=p, p->next=b, b->next=c, c->next=d 

通俗點說，插入的時候，就修改兩個結點的跟屁蟲就行啦。所以不同于數組插入和刪除操作，鏈表的插入和刪除效率很高，不需要考慮空間連續問題，所以對應的時間復雜度是O(1)。

但是反過來，如果要查詢第n個數據為誰，這個就比較麻煩了。不像數組由于內存連續，所以很輕易就知道n對應的數據。而鏈表需要一個個next查找，所以鏈表隨機訪問的效率就不如數組了，時間復雜度為O(n)。

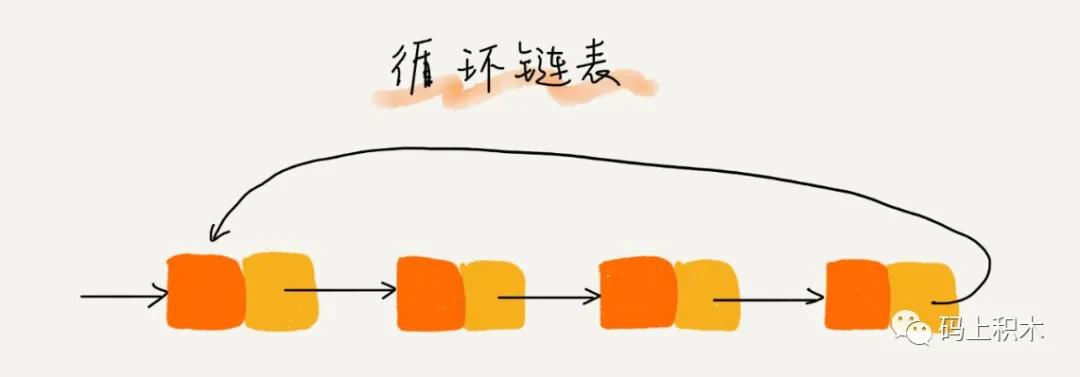
循環鏈表

 

循環鏈表和單鏈表的區別就是，尾結點指針會指向頭結點，形成一個環形，這就是循環鏈表。

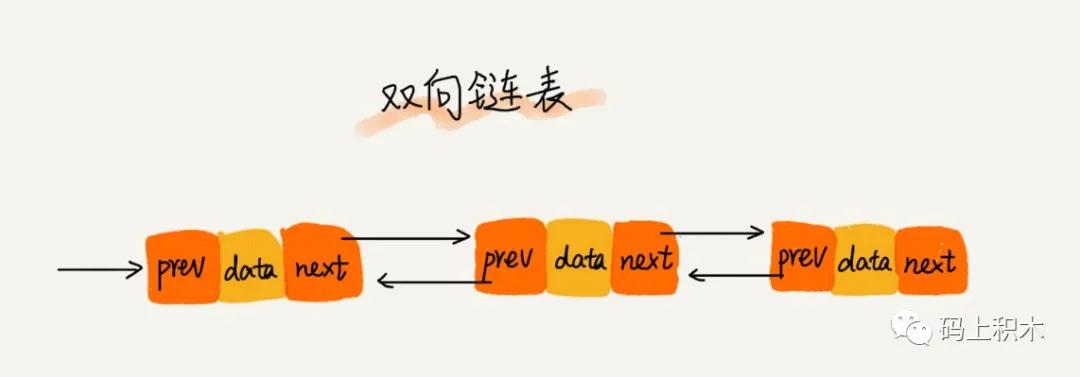
雙向鏈表

 

如圖所示，雙向鏈表和單鏈表的區別就是，每個結點不僅有下個結點的地址，還有上一個結點的地址。

這樣有什么好處呢?在特定的情境中能提高效率。比如我要在某個結點B的前面插入數據，那么我需要從頭開始便利，找到某個結點的next指向這個B的地址，然后進行數據的插入。

但是雙向鏈表則可以直接獲知結點B的前驅結點地址，大大提高了插入效率。

鏈表的基礎知識就介紹到這里了，下面看一個鏈表相關的算法題。

題目：從尾到頭打印鏈表

輸入一個鏈表的頭節點，從尾到頭反過來返回每個節點的值(用數組返回)。

示例 1：

輸入：head = [1,3,2] 輸出：[2,3,1]

限制：

0 <= 鏈表長度 <= 10000

解法一

題目意思很簡單，就是一個鏈表，現在要先從尾巴倒著打印鏈表的數字。

那我們就可以想到可以用到遞歸算法，遞歸算法其實就是兩步，先遞后歸，我們可以先傳遞到鏈表的最后一位，也就是next->null為空的時候，然后開始歸檔把數據依次輸出，即完成了從結尾開始輸出數字的需求了。

• 遞推階段：走到鏈表結尾為結束的標志。
• 歸檔階段：從結尾處一層層輸出數字，先輸出到ArrayList，在轉為數組。

不明白的可以看看代碼：

class Solution { 
    ArrayList<Integer> tmp = new ArrayList<Integer>(); 
    public int[] reversePrint(ListNode head) { 
        recur(head); 
        int[] res = new int[tmp.size()]; 
        for(int i = 0; i < res.length; i++) 
            res[i] = tmp.get(i); 
        return res; 
    } 
 
    //遞歸方法 
    void recur(ListNode head) { 
     //到鏈表結尾處，遞推結束，開始歸檔，依次輸出 
        if(head == null) return; 
        recur(head.next); 
        tmp.add(head.val); 
    } 
} 

方法消耗情況

執行用時：1 ms 
內存消耗：40.5 MB 

時間復雜度

該算法相當于遍歷了兩遍鏈表，遞推一遍，歸檔一遍，所以一共為2n。

去除常量，時間復雜度就是O(n)

空間復雜度

由于用到ArrayList和數組，所以空間復雜度也是O(n)。

解法二

第二種解法就是利用棧的特點：先入后出。(棧的知識點后面再細說)

先入后出不就是題目的需求么，從尾部倒著輸出數字。

所以我們把鏈表依次入棧，然后在依次出棧就可以完成需求了。

class Solution { 
    public int[] reversePrint(ListNode head) { 
        LinkedList<Integer> stack = new LinkedList<Integer>(); 
        while(head != null) { 
            stack.addLast(head.val); 
            head = head.next; 
        } 
        int[] res = new int[stack.size()]; 
        for(int i = 0; i < res.length; i++) 
            res[i] = stack.removeLast(); 
    return res; 
    } 
} 

方法消耗情況

執行用時：1 ms 
內存消耗：39.2 MB 

時間復雜度

同上一個算法一樣，時間復雜度就是入棧和出棧的時間，也就是O(n)。

空間復雜度

由于用到了stack和數組res，所以空間復雜度也是O(n)。

參考

https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/

https://time.geekbang.org/column/article/41013

本文轉載自微信公眾號「碼上積木」，可以通過以下二維碼關注。轉載本文請聯系碼上積木公眾號。