【動態規劃】LeetCode 題解:416-分割等和子集

大家好,我是前端西瓜哥,有三個月沒做算法題了,這次就來做一道動態規劃中難度較低的題。
題目
給你一個只包含正整數的非空數組 nums。請你判斷是否可以將這個數組分割成兩個子集,使得兩個子集的元素和相等。
示例 1:
輸入:nums = [1,5,11,5]
輸出:true
解釋:數組可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
輸入:nums = [1,2,3,5]
輸出:false
解釋:數組不能分割成兩個元素和相等的子集。
題目來源:
https://leetcode.cn/problems/partition-equal-subset-sum。
題解
動態規劃,它的模型需要符合 多階段決策最優解模型,即要推導出最后的結果,它需要經歷多個階段。
比如經典的跳樓梯,假如你要跳到第 7 階梯的樓梯,你需要先知道跳到第 5 和第 6 階梯需要走的步數。
還比如 0-1 背包問題,我們在決策是否要放入第 n 個物品,我們需要知道上一個決策完成后,書包的所有可能的重量。
這些都是 階段。我們讓多個選擇同時并行發生,產生一個個階段,并記下狀態,給下一個狀態使用。
我們回到正題。
題目意思是問能否將數組拆分成兩個子數組,這兩個子數組的和相等。
其實這就等價于,數組元素中是否存在一個子數組,它的和為原數組的總和除以 2,這時它就變成了經典 0-1 背包問題,你需要決策每個階段是否放入特定的數組元素,直到剛好為總和除以 2。
0-1 背包問題,有在書包有最大承重情況下,求放入物體的最大重量。或是提升到二維,求放入物體的最大價值。
這道題屬于前者。
先看完整的題解:
function canPartition(nums) {
const sum = nums.reduce((sum, curr) => sum + curr, 0);
if (sum % 2 === 1) return false;
const half = sum / 2;
if (nums[0] === half) return true;
const dp = new Array(nums.length);
for (let i = 0; i < dp.length; i++) {
dp[i] = new Array(half + 1).fill(false);
}
dp[0][0] = true;
if (nums[0] <= half) {
dp[0][nums[0]] = true;
}
for (let i = 1; i < dp.length; i++) {
for (let j = 0; j < dp[i].length; j++) {
if (dp[i - 1][j] === true) {
dp[i][j] = true;
if (j + nums[i] < half) {
dp[i][j + nums[i]] = true;
} else if (j + nums[i] === half) {
return true;
}
}
}
}
return false;
};
這里的要點是構建一個二維布爾值數組 dp,用來保存每個階段的狀態,對于 dp[i][j],i 表示決策第 i 個元素是否被放入,j 表示子數組總和。
所以 dp[i][j] 的意思就是在決策第 i 個元素的階段,是否存在一種可能,讓總和為 j。
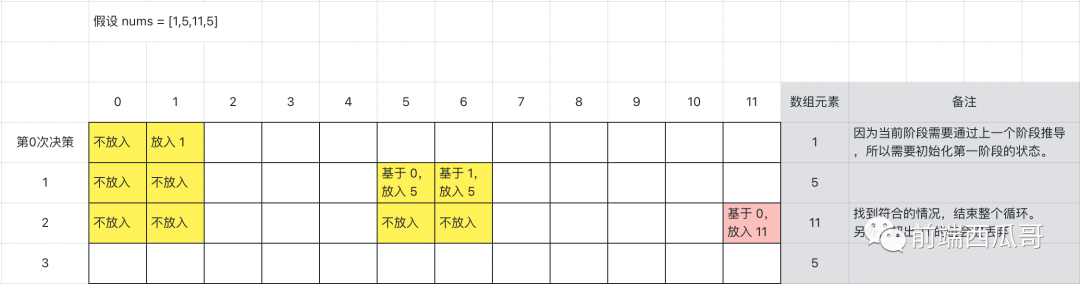
因為當前階段需要靠上一個階段推導,所以我們需要初始化第一階段的狀態:
const dp = new Array(nums.length);
for (let i = 0; i < dp.length; i++) {
dp[i] = new Array(half + 1).fill(false);
}
dp[0][0] = true;
if (nums[0] <= half) {
dp[0][nums[0]] = true;
}
然后推導下一個階段時,就遍歷上一階段的值,如果為 true,就基于它決策加入當前元素和不加入當前元素后得到的新的總和,在對應的位置標記為 true,直到和為目標值。
for (let i = 1; i < dp.length; i++) {
for (let j = 0; j < dp[i].length; j++) {
if (dp[i - 1][j] === true) {
dp[i][j] = true;
if (j + nums[i] < half) {
dp[i][j + nums[i]] = true;
} else if (j + nums[i] === half) {
return true;
}
}
}
}
其實還可以做內存優化,將二維數組轉換為一維數組,這需要用從后往前遍歷數組的技巧。
這里還用二維數組的解法,是因為它還是比較經典的,有普適性,適合用于講解。一些題目中,甚至能將優化為幾個變量,比如跳樓梯。
結尾
動態規劃,是有一定難度的算法題類型,也是面試大廠時比較常看到的題目,有掌握的必要性。





























