[[383742]]

本文轉載自微信公眾號「貝塔學JAVA」，作者Silently9527。轉載本文請聯系貝塔學JAVA公眾號。

本文已被Github倉庫收錄 https://github.com/silently9527/JavaCore

程序員常用的IDEA插件：https://github.com/silently9527/ToolsetIdeaPlugin

完全開源的淘客項目：https://github.com/silently9527/mall-coupons-server

前言

相信所有的程序員剛開始接觸到的算法都會是排序算法，因為排序在對數據處理和計算有這重要的地位，排序算法往往是其他算法的基礎;本文我們就先從初級排序算法開始學習算法。

排序算法的模板

在開始之前我們先定義一個排序算法通用的模板，在后面的排序算法都會實現這個模板

public interface SortTemplate { 
 
    void sort(Comparable[] array); 
 
    default void print(Comparable[] array) { 
        for (Comparable a : array) { 
            System.out.print(a + " "); 
        } 
    } 
 
    default boolean less(Comparable a, Comparable b) { 
        return a.compareTo(b) < 0; 
    } 
 
    default void exch(Comparable[] array, int i, int j) { 
        Comparable tmp = array[i]; 
        array[i] = array[j]; 
        array[j] = tmp; 
    } 
     
} 

• Comparable: 為了讓我們實現的排序算法更加的通用，可以排序任意的對象，所以我們這里使用了Comparable數組
• sort: 不同的排序算法實現的方式不一樣，子類自己去實現
• less: 定義的公用方法，如果a < b就返回true
• exch: 定義的公用方法，交換數組中的兩個對象
• print: 打印出數據中的每個元素

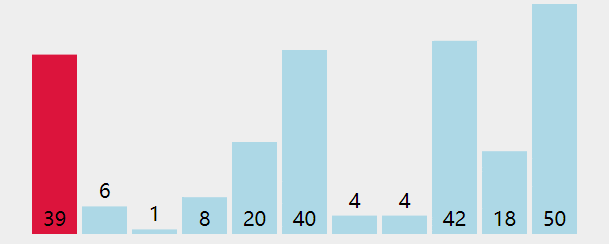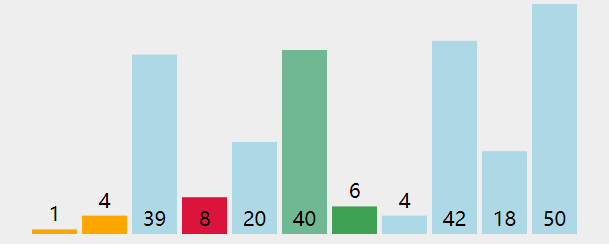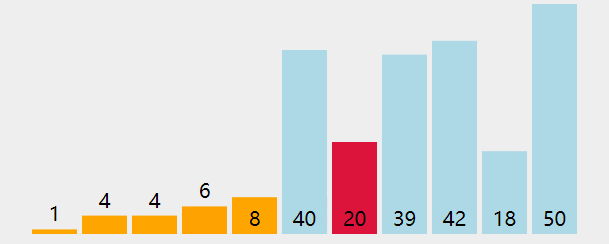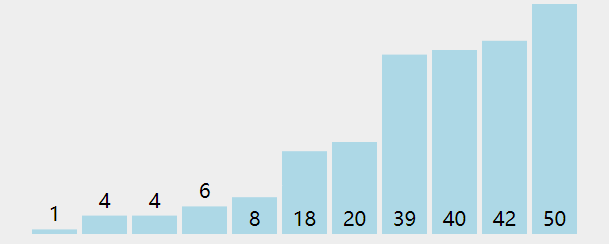
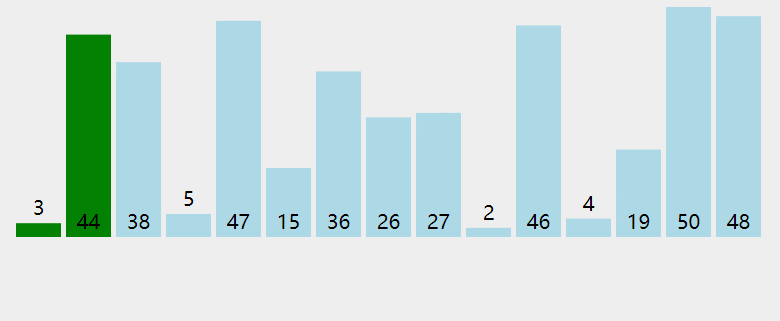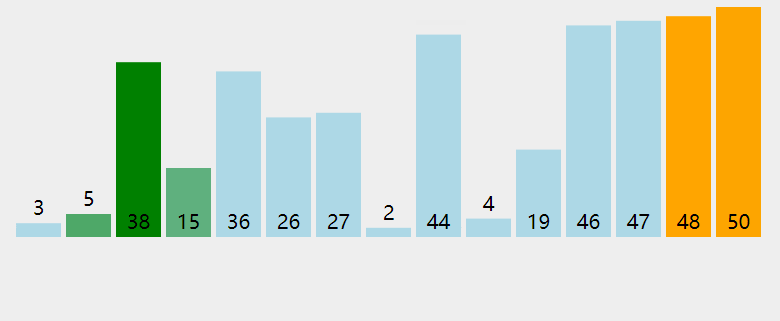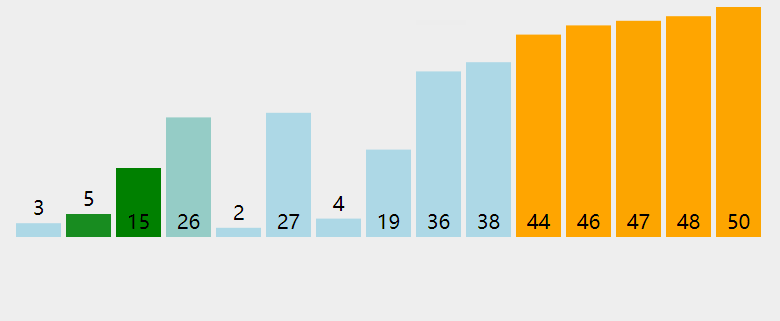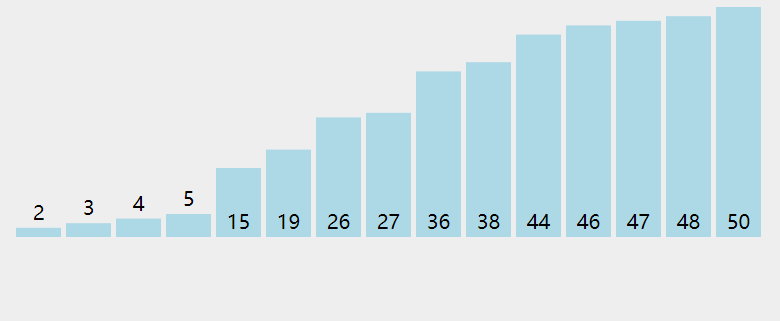
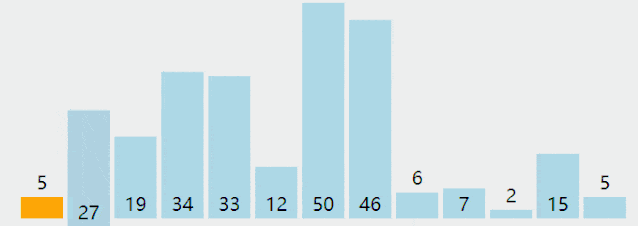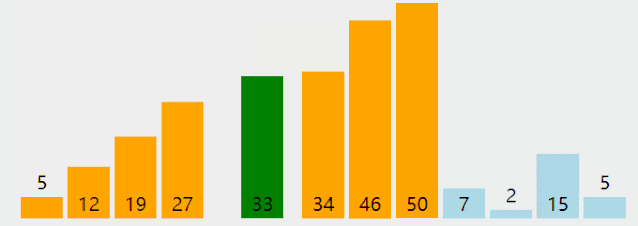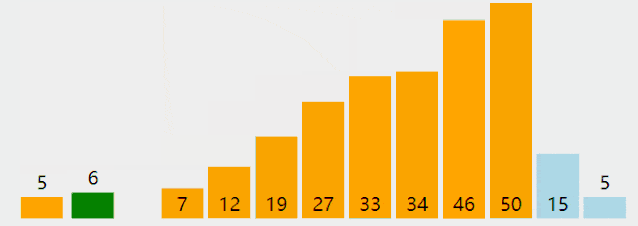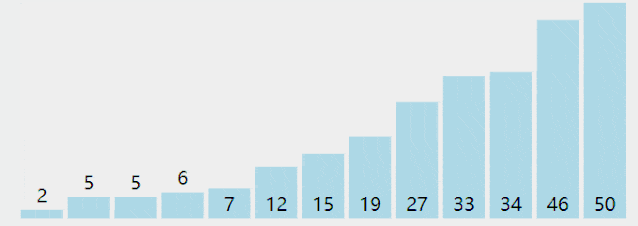
選擇排序

算法實現的思路：

• 首先找到數組中的最小元素，
• 其實將它和數組中的第一個元素進行交換，這樣就排定了一個元素;
• 再次找出剩余元素中最小的元素與數組中的第二個元素進行交換，如此反復直到所有元素都是有序的

代碼實現：

public class SelectionSort implements SortTemplate { 
 
    @Override 
    public void sort(Comparable[] array) { 
        int length = array.length; 
        for (int i = 0; i < length; i++) { 
            int min = i; 
            for (int j = i + 1; j < length; j++) { 
                if (less(array[j], array[min])) { 
                    min = j; 
                } 
            } 
            exch(array, i, min); 
        } 
    } 
 
} 

假如輸入的數組是有序的，我們會發現選擇排序運行的時候和未排序的時間一樣長!

對于N個元素的數組，使用「選擇排序的時間復雜度是O(n2)」

選擇排序的是「數據移動最少」的，交換的次數與數組的大小是線性關系，N個元素的數組需要N次交換

冒泡排序

算法實現的思路：

比較相鄰的兩個元素，如果前一個比后一個大，那么就交換兩個元素的位置

對每一組相鄰的元素執行同樣的操作，直到最后一個元素，操作完成之后就可以排定一個最大的元素

如此往復，直到數組中所有的元素都有序

代碼實現：

public class BubbleSort implements SortTemplate { 
 
    @Override 
    public void sort(Comparable[] array) { 
        int length = array.length - 1; 
        for (int i = 0; i < length; i++) { 
            for (int j = 0; j < length - i; j++) { 
                if (less(array[j + 1], array[j])) { 
                    exch(array, j, j + 1); 
                } 
            } 
        } 
    } 
 
} 

對于N個元素的數組，使用「冒泡排序的時間復雜度是O(n2)」

插入排序

想象我們在玩撲克牌時，整理撲克牌都是把每一張插入到左邊已經排好序的牌中適當的位置。插入排序的思路類似

算法實現的思路：

• 初始默認第一個元素就是有序的，當前索引的位置從0開始
• 先后移動當前索引的位置，當前索引位置左邊的元素是有序的，從后往前開始掃碼與當前索引位置元素進行比較
• 當確定當前索引位置上的元素在左邊有序適合的位置之后，插入到該位置上
• 如果當確定當前索引位置上的元素大于了已排序的最后一個元素，那么當前索引位置直接往后移動
• 如此反復，直到所有元素有序

代碼實現：

public class InsertionSort implements SortTemplate { 
 
    @Override 
    public void sort(Comparable[] array) { 
        int length = array.length; 
        for (int i = 1; i < length; i++) { 
            for (int j = i; j > 0 && less(array[j], array[j - 1]); j--) { 
                exch(array, j, j - 1); 
            } 
        } 
    } 
 
} 

從代碼的實現我們可以看出，當遇到了當前索引的元素大于了左邊有序數組的最后一個元素時，內層循環就直接結束了，所以所我們排序的數組中存在著部分有序，那么插入排序算法會很快。

考慮最糟糕的情況，如果輸入數組是一個倒置的，那么插入排序的效率和選擇排序一樣，「時間復雜度是O(n2)」

希爾排序

對于大規模的亂序數組插入排序很慢，是因為它只交換相鄰的元素，元素只能一點一點的從數組中移動到正確的位置;插入排序對于部分有序的數組排序是的效率很高;

希爾排序基于這兩個特點對插入排序進行了改進;

算法實現的思路

• 首先設置一個步長h用來分隔出子數組
• 用插入排序將h個子數組獨立排序
• 減小h步長繼續排序子數組，直到h步長為1
• 當步長為1時就成了普通的插入排序，這樣數組一定是有序的

希爾排序高效的原因，在排序之初，各個子數組都很短，子數組排序之后都是部分有序的，這兩種情況都很適合插入排序。

代碼實現：

public class ShellSort implements SortTemplate { 
 
    @Override 
    public void sort(Comparable[] array) { 
        int gap = 1; 
        int length = array.length; 
 
        while (gap < length / 3) { 
            gap = 3 * gap + 1; 
        } 
 
        while (gap >= 1) { 
            for (int i = gap; i < length; i++) { 
                for (int j = i; j >= gap && less(array[j], array[j - gap]); j -= gap) { 
                    exch(array, j, j - gap); 
                } 
            } 
            gap = gap / 3; 
        } 
    } 
 
}