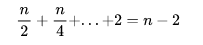Redis 有序集合使用的跳表到底是什么
1. 跳表的概念
跳表是一個動態數據結構,可以支持快速地插入、刪除、查找操作,寫起來也不怎么復雜,甚至可以替代紅黑樹。跳表的空間復雜度是 O(n),時間復雜度是 O(logn)。
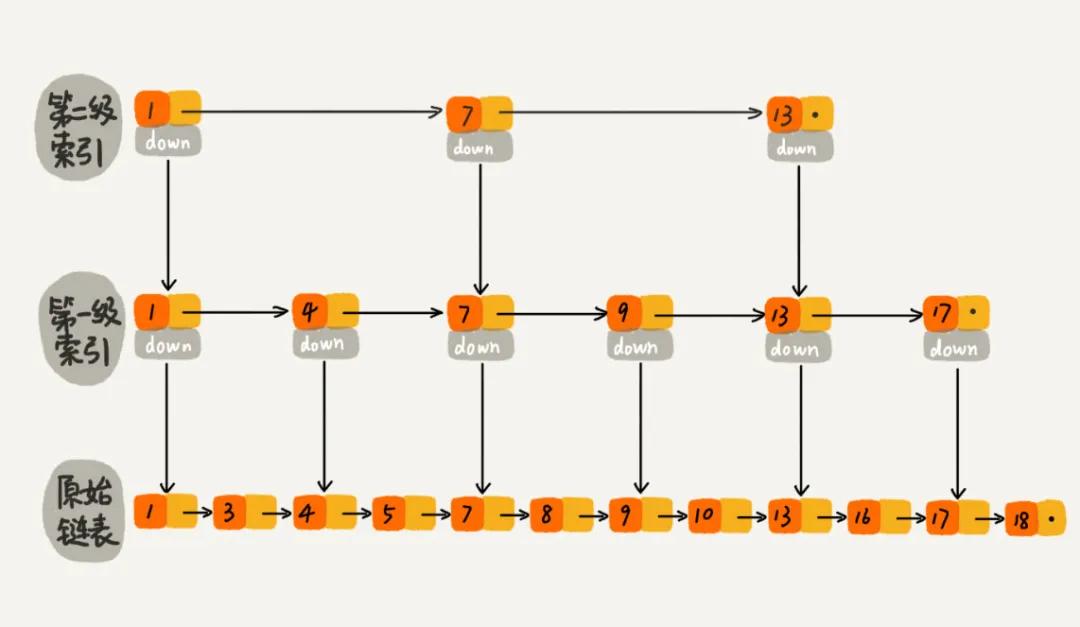
對于一個有序的單鏈表來說,如果想要查找一個數據也只能從頭到尾遍歷鏈表。為了提高查詢的效率,我們可以借助索引,即對鏈表構建一級索引,比如把每兩個鏈表節點中較小的那個節點提取為一級索引節點(對于 key value 的值來說,可以只保留 key 值),一級索引節點也可以采用同樣的方式提取為二級索引節點,如圖所示,即為跳表的結構。
針對下圖,假如想要查詢 10 這個數據,那么先在二級索引層遍歷,當遍歷到二級索引中 7 這個索引節點之后,發現后面的一個索引節點的值是 13,那么10 這個數據節點肯定是在這兩個索引節點之間。然后,我們通過 down 指針,下降到一級索引層繼續遍歷查找。這個時候遍歷到 9 這個一級索引節點,而后面一個索引節點的值是 13,那么則繼續通過 down 指針下降到原始鏈表繼續遍歷查找,從而找到 10 這個數據。
綜上所述,跳表是一個值有序的鏈表建立多級索引之后的一種數據結構,通過上述的查找方式,我們可以看到類似于二叉查找樹的查找方式,所以說跳表查找類似于鏈表的“二分查找”算法。
空間復雜度
假設原始鏈表大小為 n,那第一級鏈表有 n/2 個節點,第二季索引有 n/4 個節點,最頂層有 2 個節點。那么總共需要的索引節點個數就是
因此,跳表總的空間復雜度還是 O(n),也就說使用跳表查詢數據時,需要額外 n 個節點的存儲空間。雖然空間復雜度還是沒變,但是使用的額外空間還是有點多的。那么,可以采用以下方法來盡可能的降低索引占用的空間復雜度:可以多幾個節點抽取成一個節點,比如每 3 個節點或者 5 個節點抽取成一個節點。雖然這樣子空間復雜度還是 O(n),但實際上所需的索引節點數量少了好多。
★實際的軟件開發中,原始鏈表中存儲的有可能是很大的對象,而索引節點只需要存儲關鍵值和幾個指針,并不需要存儲對象,這個時候,索引節點所占用的額外空間相比大對象來說其實很小,可以忽略不計。”
2. 跳表的操作
2.1. 查找
單鏈表查詢的時間復雜度是 O(n),那么針對一個具有多級索引的跳表,查詢某個數據的時間復雜度是多少呢?能否提高查詢的效率呢?
假設鏈表中有 n 個節點,我們假設每兩個節點抽出一個節點作為上一級的索引節點,那么第一級的索引節點個數是 n/2,第二級的索引節點個數是 n/2^2。依次類推,第 k 級的索引節點個數是 n/2^k。假設索引層最高有 h 級,而最高層的索引節點有 2 個節點,那么得到 ,加上原始鏈表這一層,一共有 層。
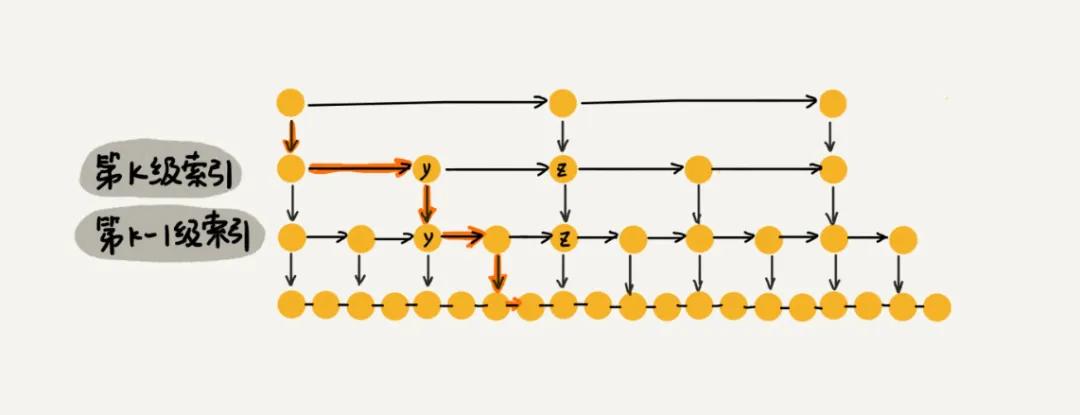
我們在跳表中查詢某個數據的時候,如果每一層都要編譯 m 個,那么跳表一個數據的時間復雜度就是 O(mlogn)。由于我們是每兩個節點抽出一個節點,而且最高層也只有兩個節點,所以每一層最多比較 3 個節點。比如我們要查找的數據是 x,當在第 k 級索引層遍歷到 y 節點之后,發現 x 大于 y 但是小于 y 后面的 z 節點,那么則通過 y 的down 指針從 k 級索引下降到 k-1 級索引,而在 k-1 級索引中最多只需要遍歷 3 個節點即可。
因此,在跳表中查詢數據的時間復雜度是 O(logn),這個時間復雜度和二分查找是一樣的。不過,這種查詢效率的提升,提前是建立了很多級索引,使用了空間換時間的設計思路。
2.2. 插入
在單鏈表中,假如定位到了要插入的位置,那么插入節點這個操作的時間復雜度很低,為 O(1)。但是要定位到插入的位置的時間復雜度是 O(n),比如原始鏈表中數據有序,那么需要遍歷鏈表才能找到要插入的位置。
對于跳表來說,由于查找某個節點的時間復雜度是 O(logn),而插入實際上就是鏈表中的插入,因此插入操作的時間復雜度也就是 O(logn)。
2.3. 刪除
刪除操作也是類似的,但是如果這個節點在索引中也有出現的話,除了要刪除原始鏈表中的節點之外,還要刪除索引中的。由于刪除節點需要前驅節點,因此使用雙向鏈表的話,可以很方便的刪除一個節點。
綜上,刪除操作的時間復雜度也可以做到 O(logn)。
2.4. 索引更新
當我們不停地往跳表中插入數據而不更新索引節點的話,那么 2 個索引節點之間的數據可能會非常的多。極端情況下,跳表可能會退化為單鏈表。因此,我們需要某種手段來維護索引與原始鏈表大小之間的平衡,也就是說如果鏈表中的節點變多了,索引節點也相應地增加一些,避免查找、插入、刪除的性能下降。
跳表通過隨機函數的方式來維護這種平衡性。當我們往跳表中插入數據的時候,我們通過一個隨機函數,來決定將這個在哪幾層索引層中添加。比如隨機函數生成了值 k,那么我們就在第一級到第 k 級這 k 級索引中添加相應的索引節點。
★對于平衡二叉樹來說,比如紅黑樹、AVL,它們是通過左右旋的方式來保持左右子樹的平衡。”
3. 應用
Redis 中的有序集合就是用跳表來實現的,另外還用到了散列表。為什么使用跳表而不是紅黑樹實現呢?最主要的是跳表它支持區間查找。
Redis 中的有序集合支持的核心操作中主要有:
- 插入、刪除、查找一個數據;
- 按照區間查找數據(比如查找值在 [100, 356] 之間的數據)
- 迭代輸出有序序列
其中插入、刪除、查找操作,紅黑樹也可以很快完成,時間復雜度也是 O(logn)。但是按照區間來查找數據這個操作,紅黑樹的效率沒有跳表高。跳表可以做到 O(logn) 的時間復雜度定位區間的起點,然后在原始鏈表中順序往后遍歷就可以了。
★實際上,在有序集合中,每個成員對象有兩個重要的屬性:key 和 value。我們有時候不僅需要通過 value 來查找數據,還會通過 key 來查找數據。我們可以按照 value 將成員對象組織成跳表的結構,那么此時根據 value 來查找對象很方便,但是當我們想要通過 key 查找對象時又會很麻煩。那么,我們可以結合散列表,也就相當于把散列表和跳表結合。此時,根據 key 來查找、刪除、插入一個成員對象的時間復雜度就變成了 O(1)。”
4. 總結
跳表是一種動態數據結構,使用了空間換時間的設計思想來提高查詢的效率,簡單來說就是在原始鏈表的基礎之上構建了多級索引層來提高查詢的效率,在查找方式上有點類似于二分查找。
綜上,跳表的查詢、插入、刪除的時間復雜度都是 O(logn),而空間復雜度是 O(n)。
5. 參考
https://juejin.im/post/6844903446475177998
本文轉載自微信公眾號「多選參數」,可以通過以下二維碼關注。轉載本文請聯系多選參數公眾號。