給女朋友這樣講全排列、組合、子集問題,下次再也不鬧了
本文轉載自微信公眾號「bigsai」,作者bigsai。轉載本文請聯(lián)系bigsai公眾號。
前言
Hello,大家好,long time no see!在刷題和面試過程中,我們經(jīng)常遇到一些排列組合類的問題,而全排列、組合、子集等問題更是非常經(jīng)典問題。本篇文章就帶你徹底搞懂全排列!
求全排列?
全排列即:n個元素取n個元素(所有元素)的所有排列組合情況。
求組合?
組合即:n個元素取m個元素的所有組合情況(非排列)。
求子集?
子集即:n個元素的所有子集(所有可能的組合情況)。
總的來說全排列數(shù)值個數(shù)是所有元素,不同的是排列順序;而組合是選取固定個數(shù)的組合情況(不看排列);子集是對組合拓展,所有可能的組合情況(同不考慮排列)。
當然,這三種問題,有相似之處又略有所不同,我們接觸到的全排列可能更多,所以你可以把組合和子集問題認為是全排列的拓展變形。且問題可能會遇到待處理字符是否有重復的情況。采取不同的策略去去重也是相當關鍵和重要的!在各個問題的具體求解上方法可能不少,在全排列上最流行的就是鄰里互換法和回溯法,而其他的組合和子集問題是經(jīng)典回溯問題。而本篇最重要和基礎的就是要掌握這兩種方法實現(xiàn)的無重復全排列,其他的都是基于這個進行變換和拓展。
全排列問題
全排列,元素總數(shù)為最大,不同是排列的順序。
無重復序列的全排列
這個問題剛好在力扣46題是原題的,大家學完可以去a試試。
問題描述:
給定一個 沒有重復 數(shù)字的序列,返回其所有可能的全排列。
示例:
- 輸入: [1,2,3]
- 輸出:
- [
- [1,2,3],
- [1,3,2],
- [2,1,3],
- [2,3,1],
- [3,1,2],
- [3,2,1]
- ]
回溯法實現(xiàn)無重復全排列
回溯算法用來解決搜索問題,而全排列剛好也是一種搜索問題,先回顧一下什么是回溯算法:
回溯算法實際上一個類似枚舉的搜索嘗試過程,主要是在搜索嘗試過程中尋找問題的解,當發(fā)現(xiàn)已不滿足求解條件時,就“回溯”返回,嘗試別的路徑.
而全排列剛好可以使用試探的方法去枚舉所有中可能性。一個長度為n的序列或者集合。它的所有排列組合的可能性共有n!種。具體的試探策略如下:
- 從待選集合中選取第一個元素(共有n種情況),并標記該元素已經(jīng)被使用不能再使用。
- 在步驟1的基礎上進行遞歸到下一層,從剩余n-1個元素中按照1的方法找到一個元素并標記,繼續(xù)向下遞歸。
- 當所有元素被標記后,順序收集被標記的元素存儲到結果中,當前層遞歸結束,回到上一層(同時將當前層標記的元素清除標記)。這樣一直執(zhí)行到最后。
回溯的流程如果從偽代碼流程大致為這樣:
- 遞歸函數(shù):
- 如果集合所有元素被標記:
- 將臨時儲存添加到結果集中
- 否則:
- 從集合中未標記的元素中選取一個存儲到臨時集合中
- 標記該元素被使用
- 下一層遞歸函數(shù)
- (這層遞歸結束)標記該元素未被使用
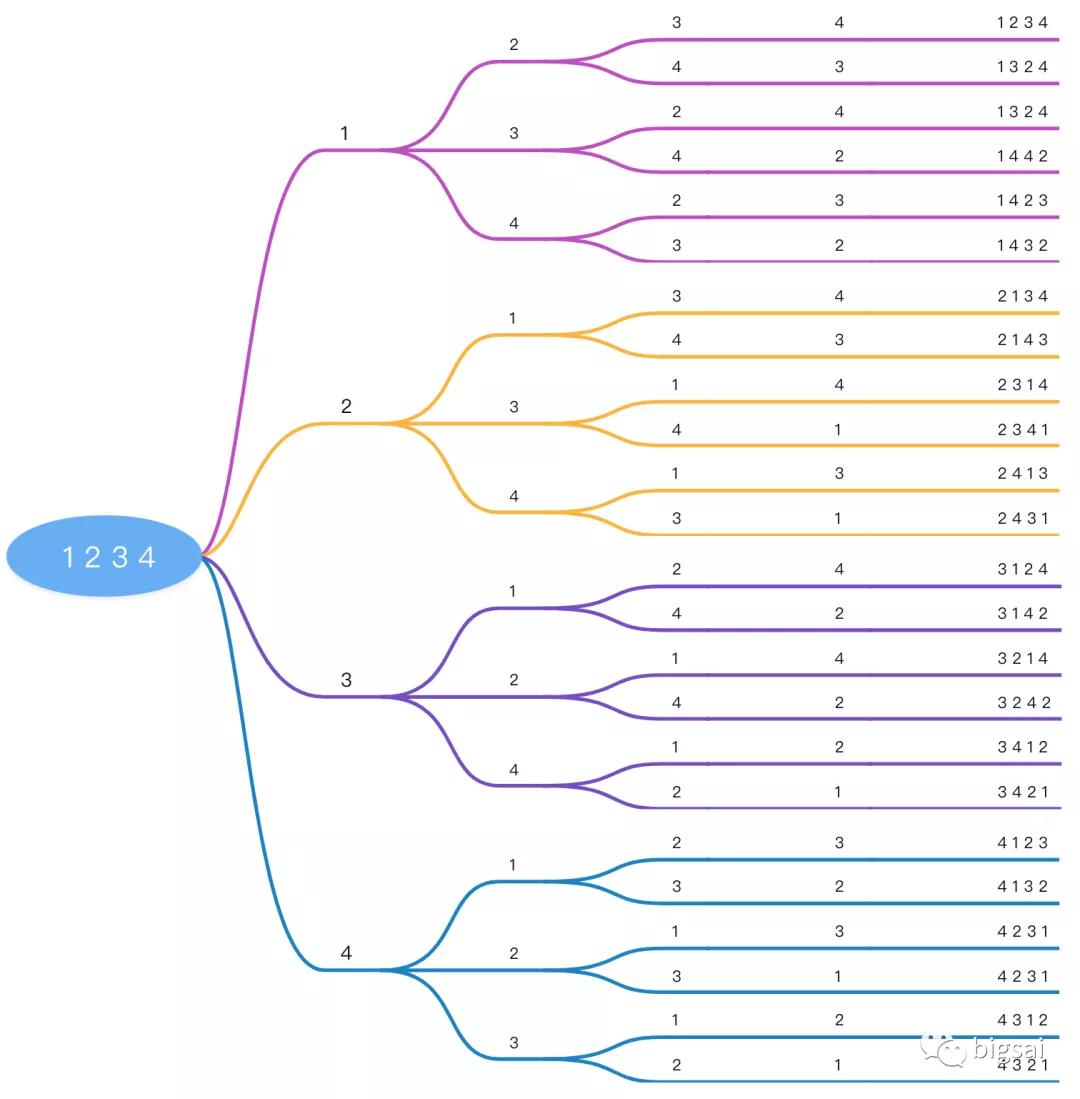
如果用序列 1 2 3 4來表示這么回溯的一個過程,可以用這張圖來顯示:
回溯過程
用代碼來實現(xiàn)思路也是比較多的,需要一個List去存儲臨時結果是很有必要的,但是對于原集合我們標記也有兩種處理思路,第一種是使用List存儲集合,使用過就移除然后遞歸下一層,遞歸完畢后再添加到原來位置。另一種思路就是使用固定數(shù)組存儲,使用過對應位置使用一個boolean數(shù)組對應位置標記一下,遞歸結束后再還原。因為List頻繁查找插入刪除效率一般比較低,所以我們一般使用一個boolean數(shù)組去標記該位置元素是否被使用。
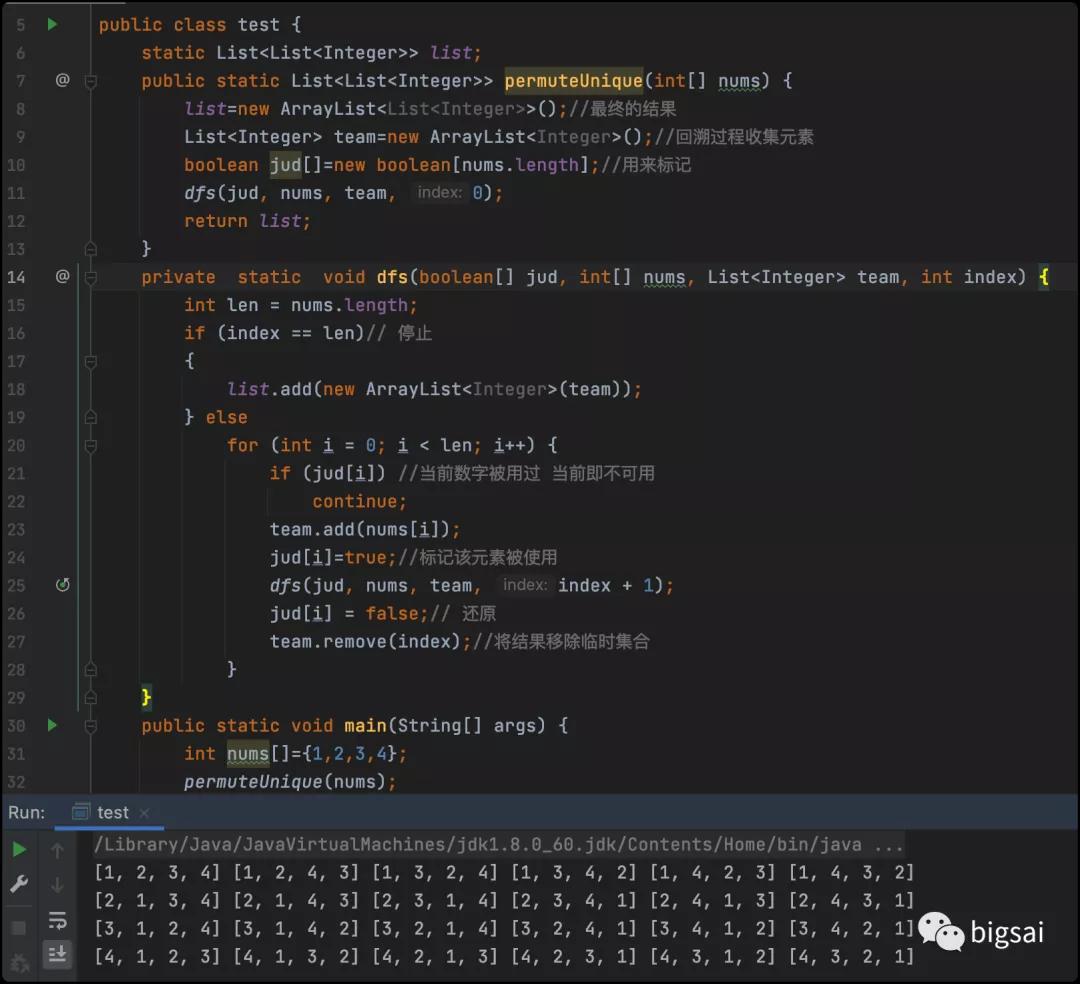
具體實現(xiàn)的代碼為:
- List<List<Integer>> list;
- public List<List<Integer>> permuteUnique(int[] nums) {
- list=new ArrayList<List<Integer>>();//最終的結果
- List<Integer> team=new ArrayList<Integer>();//回溯過程收集元素
- boolean jud[]=new boolean[nums.length];//用來標記
- dfs(jud, nums, team, 0);
- return list;
- }
- private void dfs(boolean[] jud, int[] nums, List<Integer> team, int index) {
- int len = nums.length;
- if (index == len)// 停止
- {
- list.add(new ArrayList<Integer>(team));
- } else
- for (int i = 0; i < len; i++) {
- if (jud[i]) //當前數(shù)字被用過 當前即不可用
- continue;
- team.add(nums[i]);
- jud[i]=true;//標記該元素被使用
- dfs(jud, nums, team, index + 1);
- jud[i] = false;// 還原
- team.remove(index);//將結果移除臨時集合
- }
- }
修改一下輸出的結果和上面思維導圖也是一致的:
鄰里互換法實現(xiàn)無重復全排列
回溯的測試是試探性填充,是對每個位置進行單獨考慮賦值。而鄰里互換的方法雖然是也是遞歸實現(xiàn)的,但是他是一種基于交換的策略和思路。而理解起來也是非常簡單,鄰里互換的思路是從左向右進行考慮。
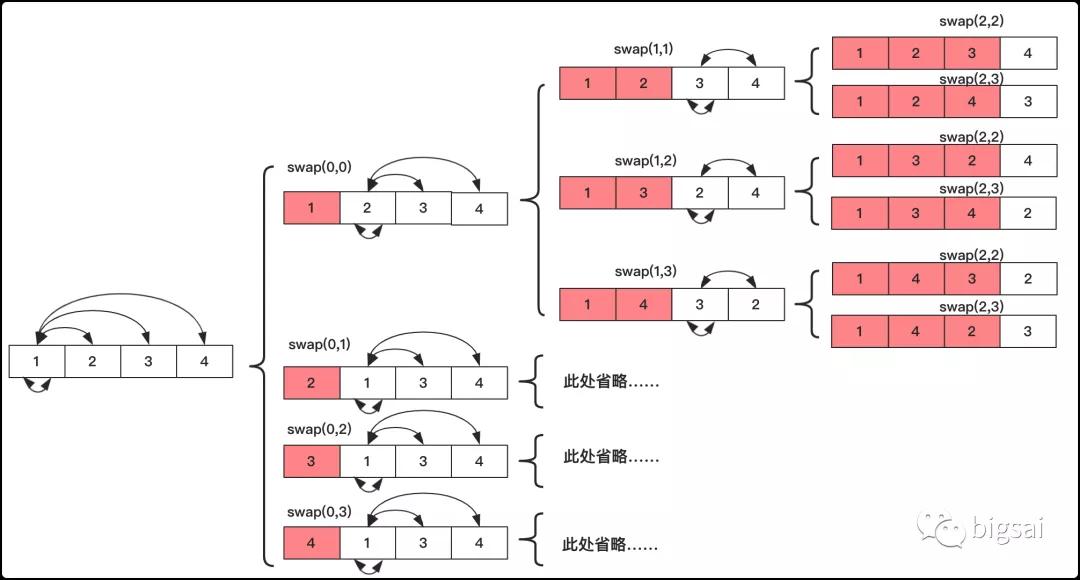
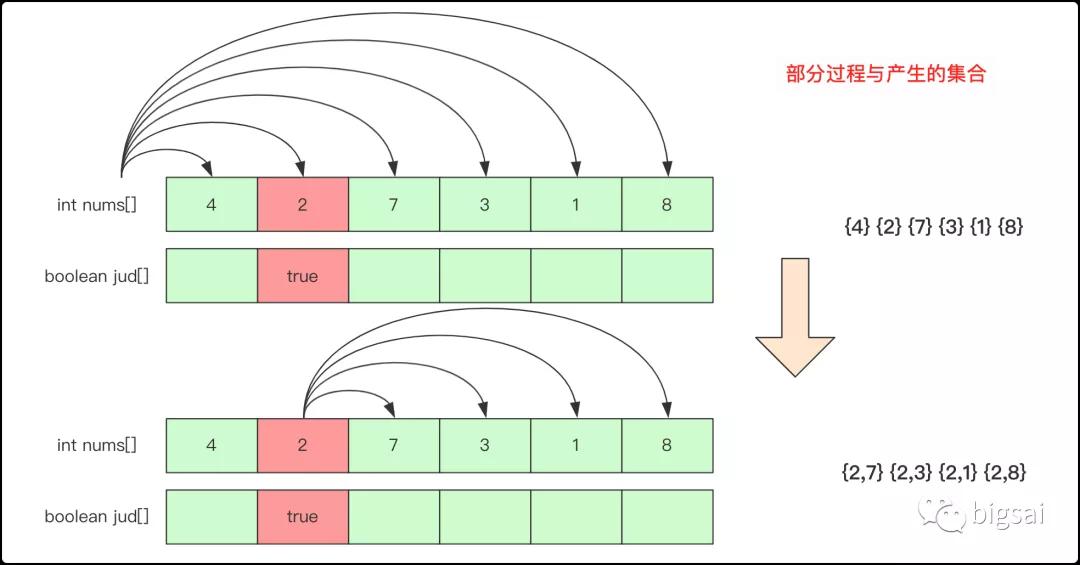
因為序列是沒有重復的,我們開始將數(shù)組分成兩個部分:暫時確定部分和未確定部分。開始的時候均是未確定部分,我們需要妥善處理的就是未確定部分。在未確定部分的序列中,我們需要讓后面未確定的每一位都有機會處在未確定的首位,所以未確定部分的第一個元素就要和每一個依次進行交換(包括自己),交換完成之后再向下進行遞歸求解其他的可能性,求解完畢之后要交換回來(還原)再和后面的進行交換。這樣當遞歸進行到最后一層的時候就將數(shù)組的值添加到結果集中。如果不理解可以參考下圖進行理解:
鄰里互換部分過程
實現(xiàn)代碼為:
- class Solution {
- public List<List<Integer>> permute(int[] nums) {
- List<List<Integer>>list=new ArrayList<List<Integer>>();
- arrange(nums,0,nums.length-1,list);
- return list;
- }
- private void arrange(int[] nums, int start, int end, List<List<Integer>> list) {
- if(start==end)//到最后一個 添加到結果中
- {
- List<Integer>list2=new ArrayList<Integer>();
- for(int a:nums)
- {
- list2.add(a);
- }
- list.add(list2);
- }
- for(int i=start;i<=end;i++)//未確定部分開始交換
- {
- swap(nums,i,start);
- arrange(nums, start+1, end, list);
- swap(nums, i, start);//還原
- }
- }
- private void swap(int[] nums, int i, int j) {
- int team=nums[i];
- nums[i]=nums[j];
- nums[j]=team;
- }
- }
那么鄰里互換和回溯求解的全排列有什么區(qū)別呢?首先回溯法求得的全排列如果這個序列有序得到的結果是字典序的,因為其策略是填充,先小后大有序,而鄰里互換沒有這個特征。其次鄰里互換在這種情況下的效率要高于回溯算法的,雖然量級差不多但是回溯算法需要維護一個集合頻繁增刪等占用一定的資源。
有重復序列的全排列
有重復對應的是力扣第47題 ,題目描述為:
給定一個可包含重復數(shù)字的序列 nums ,按任意順序 返回所有不重復的全排列。
示例 1:
- 輸入:nums = [1,1,2]
- 輸出:
- [[1,1,2],
- [1,2,1],
- [2,1,1]]
示例 2:
- 輸入:nums = [1,2,3]
- 輸出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
這個和上面不重復的全排列略有不同,這個輸入數(shù)組中可能包含重復的序列,我們怎么樣采取合適的策略去重復才是至關重要的。我們同樣針對回溯和鄰里互換兩種方法進行分析。
回溯剪枝法
因為回溯完整的比直接遞歸慢,所以剛開始并沒有考慮使用回溯算法,但是這里用回溯剪枝相比遞歸鄰里互換方法更好一些,對于不使用哈希去重的方法,首先進行排序預處理是沒有懸念的,而回溯法去重的關鍵就是避免相同的數(shù)字因為相對次序問題造成重復,所以在這里相同數(shù)字在使用上相對位置必須不變,而具體剪枝條的規(guī)則如下:
- 先對序列進行排序
- 試探性將數(shù)據(jù)放到當前位置
- 如果當前位置數(shù)字已經(jīng)被使用,那么不可使用
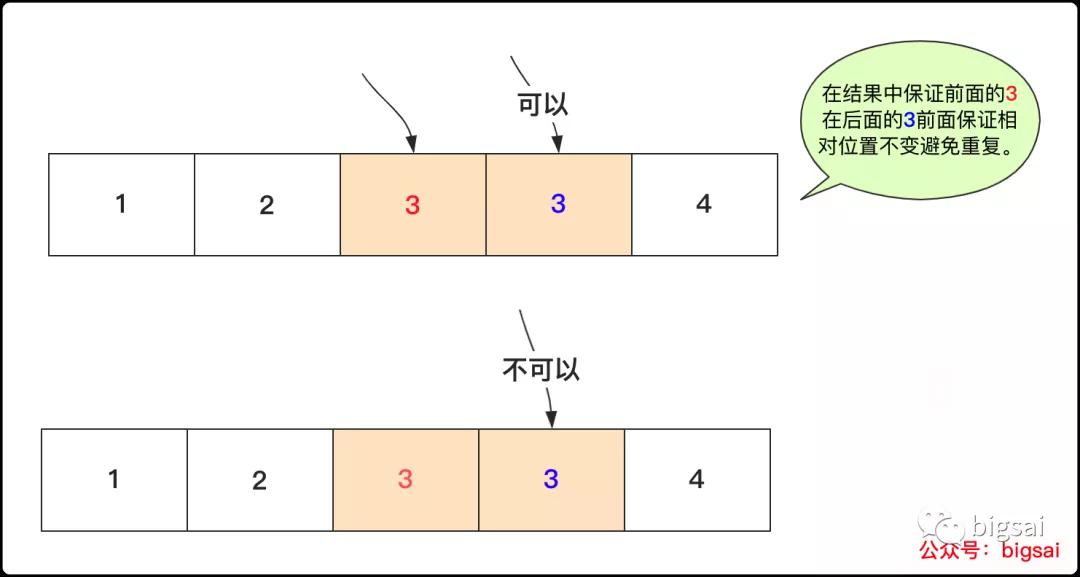
- 如果當前數(shù)字和前一個相等但是前一個沒有被使用,那么當前不能使用,需要使用前一個數(shù)字。
回溯選取策略
思路很簡單,實現(xiàn)起來也很簡單:
- List<List<Integer>> list;
- public List<List<Integer>> permuteUnique(int[] nums) {
- list=new ArrayList<List<Integer>>();
- List<Integer> team=new ArrayList<Integer>();
- boolean jud[]=new boolean[nums.length];
- Arrays.sort(nums);
- dfs(jud, nums, team, 0);
- return list;
- }
- private void dfs(boolean[] jud, int[] nums, List<Integer> team, int index) {
- // TODO Auto-generated method stub
- int len = nums.length;
- if (index == len)// 停止
- {
- list.add(new ArrayList<Integer>(team));
- } else
- for (int i = 0; i < len; i++) {
- if (jud[i]||(i>0&&nums[i]==nums[i-1]&&!jud[i-1])) //當前數(shù)字被用過 或者前一個相等的還沒用,當前即不可用
- continue;
- team.add(nums[i]);
- jud[i]=true;
- dfs(jud, nums, team, index + 1);
- jud[i] = false;// 還原
- team.remove(index);
- }
- }
鄰里互換法
我們在執(zhí)行遞歸全排列的時候,主要考的是要把重復的情況搞下去,鄰里互換又要怎么去重呢?
使用HashSet這種方式這里就不討論啦,我們在進行交換swap的時候從前往后,前面的確定之后就不會在動,所以我們要慎重考慮和誰交換。比如1 1 2 3第一個數(shù)有三種情況而不是四種情況(兩個1 1 2 3為一個結果):
- 1 1 2 3 // 0 0位置交換
- 2 1 1 3 // 0 2位置交換
- 3 1 2 1 // 0 3位置交換
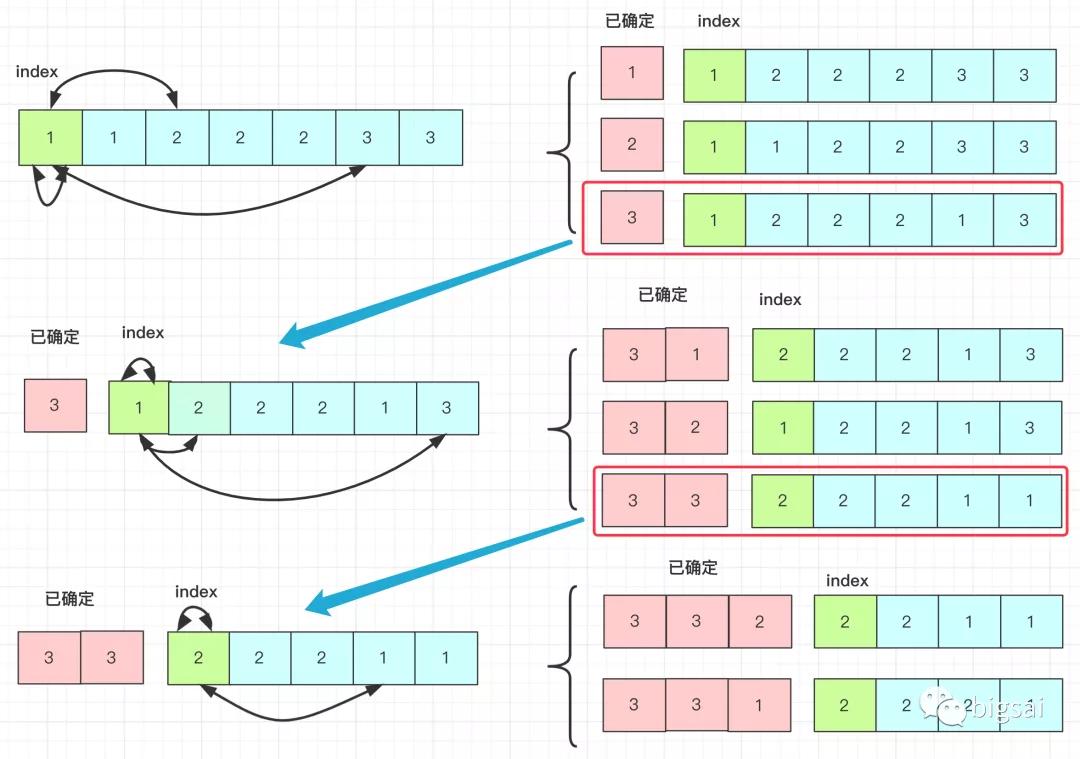
另外比如3 1 1序列,3和自己交換,和后面兩個1只能和其中一個進行交換,我們這里可以約定和第一個出現(xiàn)的進行交換,我們看一個圖解部分過程:
鄰里互換一個過程
所以,當我們從一個index開始的時候要記住以下的規(guī)則:同一個數(shù)只交換一次(包括值等于自己的數(shù))。在判斷后面值是否出現(xiàn)的時候,你可以遍歷,也可以使用hashSet().當然這種方法的痛點就是判斷后面出現(xiàn)的數(shù)字效率較低。所以在可能重復的情況這種方法效率一般般。
具體實現(xiàn)的代碼為:
- public List<List<Integer>> permuteUnique(int[] nums) {
- List<List<Integer>> list=new ArrayList<List<Integer>>();
- arrange(nums, 0, nums.length-1, list);
- return list;
- }
- private void arrange(int[] nums, int start, int end, List<List<Integer>> list) {
- if(start==end)
- {
- List<Integer>list2=new ArrayList<Integer>();
- for(int a:nums)
- {
- list2.add(a);
- }
- list.add(list2);
- }
- Set<Integer>set=new HashSet<Integer>();
- for(int i=start;i<=end;i++)
- {
- if(set.contains(nums[i]))
- continue;
- set.add(nums[i]);
- swap(nums,i,start);
- arrange(nums, start+1, end, list);
- swap(nums, i, start);
- }
- }
- private void swap(int[] nums, int i, int j) {
- int team=nums[i];
- nums[i]=nums[j];
- nums[j]=team;
- }
組合問題
組合問題可以認為是全排列的變種,問題描述(力扣77題):
給定兩個整數(shù) n 和 k,返回 1 … n 中所有可能的 k 個數(shù)的組合。
示例:
- 輸入: n = 4, k = 2
- 輸出:
- [
- [2,4],
- [3,4],
- [2,3],
- [1,2],
- [1,3],
- [1,4],
- ]
分析:
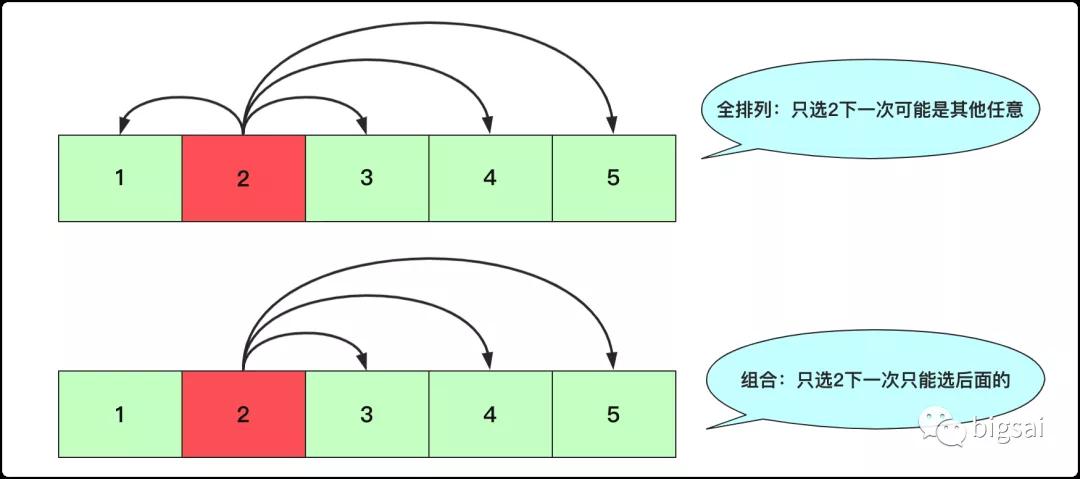
這個問題經(jīng)典回溯問題。組合需要記住只看元素而不看元素的順序,比如a b和b a是同一個組合。要避免這樣的重復是核心,而避免這樣的重復,需要借助一個int類型保存當前選擇元素的位置,下次只能遍歷選取下標位置后面的數(shù)字,而k個數(shù),可以通過一個數(shù)字類型來記錄回溯到當前層處理數(shù)字的個數(shù)來控制。
全排列和組合的一些區(qū)別
具體實現(xiàn)也很容易,需要創(chuàng)建一個數(shù)組儲存對應數(shù)字,用boolean數(shù)組判斷對應位置數(shù)字是否使用,這里就不用List存儲數(shù)字了,最后通過判斷boolean數(shù)組將數(shù)值添加到結果中也是可行的。實現(xiàn)代碼為:
- class Solution {
- public List<List<Integer>> combine(int n, int k) {
- List<List<Integer>> valueList=new ArrayList<List<Integer>>();//結果
- int num[]=new int[n];//數(shù)組存儲1-n
- boolean jud[]=new boolean[n];//用于判斷是否使用
- for(int i=0;i<n;i++)
- {
- num[i]=i+1;
- }
- List<Integer>team=new ArrayList<Integer>();
- dfs(num,-1,k,valueList,jud,n);
- return valueList;
- }
- private void dfs(int[] num,int index, int count,List<List<Integer>> valueList,boolean jud[],int n) {
- if(count==0)//k個元素滿
- {
- List<Integer>list=new ArrayList<Integer>();
- for(int i=0;i<n;i++)
- {
- if (jud[i]) {
- list.add(i+1);
- }
- }
- valueList.add(list);
- }
- else {
- for(int i=index+1;i<n;i++)//只能在index后遍歷 回溯向下
- {
- jud[i]=true;
- dfs(num, i, count-1, valueList,jud,n);
- jud[i]=false;//還原
- }
- }
- }
- }
子集
子集問題和組合有些相似。這里講解數(shù)組中無重復和有重復的兩種情況。
無重復數(shù)組子集
問題描述(力扣78題):
給你一個整數(shù)數(shù)組 nums ,數(shù)組中的元素 互不相同 。返回該數(shù)組所有可能的子集(冪集)。
解集 不能 包含重復的子集。你可以按 任意順序 返回解集。
示例 1:
- 輸入:nums = [1,2,3]
- 輸出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
示例 2:
- 輸入:nums = [0]
- 輸出:[[],[0]]
提示:
1 <= nums.length <= 10
-10 <= nums[i] <= 10
nums 中的所有元素 互不相同
子集和上面的組合有些相似,當然我們不需要判斷有多少個,只需要按照組合回溯的策略遞歸進行到最后,每進行的一次遞歸函數(shù)都是一種情況都要加入到結果中(因為采取的策略不會有重復的情況)。
實現(xiàn)的代碼為:
- class Solution {
- public List<List<Integer>> subsets(int[] nums) {
- List<List<Integer>> valueList=new ArrayList<List<Integer>>();
- boolean jud[]=new boolean[nums.length];
- List<Integer>team=new ArrayList<Integer>();
- dfs(nums,-1,valueList,jud);
- return valueList;
- }
- private void dfs(int[] num,int index,List<List<Integer>> valueList,boolean jud[]) {
- {//每進行遞歸函數(shù)都要加入到結果中
- List<Integer>list=new ArrayList<Integer>();
- for(int i=0;i<num.length;i++)
- {
- if (jud[i]) {
- list.add(num[i]);
- }
- }
- valueList.add(list);
- }
- {
- for(int i=index+1;i<num.length;i++)
- {
- jud[i]=true;
- dfs(num, i, valueList,jud);
- jud[i]=false;
- }
- }
- }
- }
有重復數(shù)組子集
題目描述(力扣90題):
給定一個可能包含重復元素的整數(shù)數(shù)組 nums,返回該數(shù)組所有可能的子集(冪集)。
說明:解集不能包含重復的子集。
示例:
- 輸入: [1,2,2]
- 輸出:
- [
- [2],
- [1],
- [1,2,2],
- [2,2],
- [1,2],
- []
- ]
和上面無重復數(shù)組求子集不同的是這里面可能會出現(xiàn)重復的元素。我們需要在結果中過濾掉重復的元素。
首先,子集問題無疑是使用回溯法求得結果,首先分析如果序列沒有重復的情況,我們會借助一個boolean[]數(shù)組標記使用過的元素和index表示當前的下標,在進行回溯的時候我們只向后進行遞歸并且將枚舉到的那個元素boolean[index]置為true(回來的時候復原)。每次遞歸收集boolean[]數(shù)組中true的元素為其中一個子集。
在這里插入圖片描述
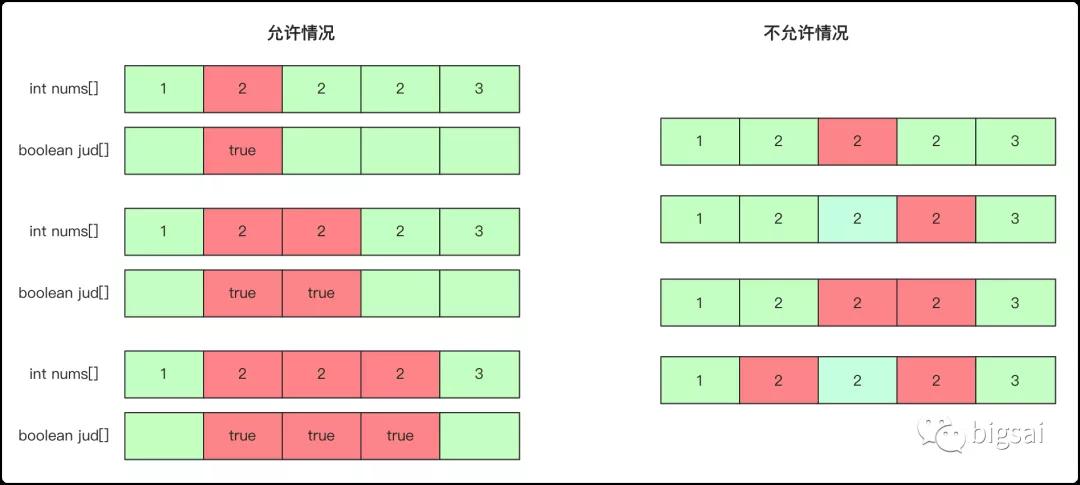
而有重復元素的處理上,和前面全排列的處理很相似,首先進行排序,然后在進行遞歸處理的時候遇到相同元素只允許從第一位連續(xù)使用而不允許跳著使用,所以在遞歸向下時候需要判斷是否滿足條件(第一個元素或和前一個不同或和前一個同且前一個已使用),具體可以參考這張圖:
實現(xiàn)代碼為:
- class Solution {
- public List<List<Integer>> subsetsWithDup(int[] nums) {
- Arrays.sort(nums);
- boolean jud[]=new boolean[nums.length];
- List<List<Integer>> valueList=new ArrayList<List<Integer>>();
- dfs(nums,-1,valueList,jud);
- return valueList;
- }
- private void dfs(int[] nums, int index, List<List<Integer>> valueList, boolean[] jud) {
- // TODO Auto-generated method stub
- List<Integer>list=new ArrayList<Integer>();
- for(int i=0;i<nums.length;i++)
- {
- if (jud[i]) {
- list.add(nums[i]);
- }
- }
- valueList.add(list);
- for(int i=index+1;i<nums.length;i++)
- {//第一個元素 或 當前元素不和前面相同 或者相同且前面被使用了可以繼續(xù)進行
- if((i==0)||(nums[i]!=nums[i-1])||(i>0&&jud[i-1]&&nums[i]==nums[i-1]))
- {
- jud[i]=true;
- dfs(nums, i, valueList,jud);
- jud[i]=false;
- }
- }
- }
- }
結語
到這里,本篇的全排列、組合、子集問題就介紹到這里啦,尤其要注意問題處理去重的思路和策略。當然和這類似的問題也是很多啦,多刷一刷就可以很好的掌握,后面敬請期待!