矩陣乘法作為一種基本的數(shù)學(xué)運算，在計算機科學(xué)領(lǐng)域有著非常廣泛的應(yīng)用，矩陣乘法的快速算法對科學(xué)計算有著極為重要的意義。自 1969 年 Strassen 算法開始，人們意識到了快速算法的存在，開始了長達(dá)數(shù)十年的探索研究。

當(dāng)你擁有兩個大小一致的矩陣時，則可以將它們相乘得到第三個矩陣。例如，一對 2×2 矩陣的乘積也將是 2×2 矩陣，包含 4 個元素。即一對 n×n 矩陣的乘積是具有 n^2 個元素的另一個 n×n 矩陣。

因此，矩陣乘法至少需要 n^2 步，人們理想中的計算復(fù)雜度也就是 O(n^2)。

2020 年 10 月，來自哈佛大學(xué)與 MIT 的兩位研究者發(fā)表了一篇論文，他們創(chuàng)建了有史以來矩陣相乘的最快算法，相比于之前最快算法，計算復(fù)雜度下降了 10 萬分之一。其中，論文一作 Josh Alman 是哈佛大學(xué)的博士后研究生，主要研究算法設(shè)計與復(fù)雜度理論。二作 Vassilevska Williams 是 MIT 計算機科學(xué)與人工智能實驗室（CSAIL）副教授，致力于將組合和圖論工具應(yīng)用于計算領(lǐng)域。

論文地址：https://arxiv.org/pdf/2010.05846.pdf

矩陣乘法的運算方法

為了了解該過程及其改進(jìn)方法，我們首先來看一對 2 x 2 的矩陣，分別為矩陣 A 和矩陣 B。在計算它們的乘積時，需要使用矩陣 A 的對應(yīng)行和矩陣 B 的對應(yīng)列。具體運算方法如下圖所示：

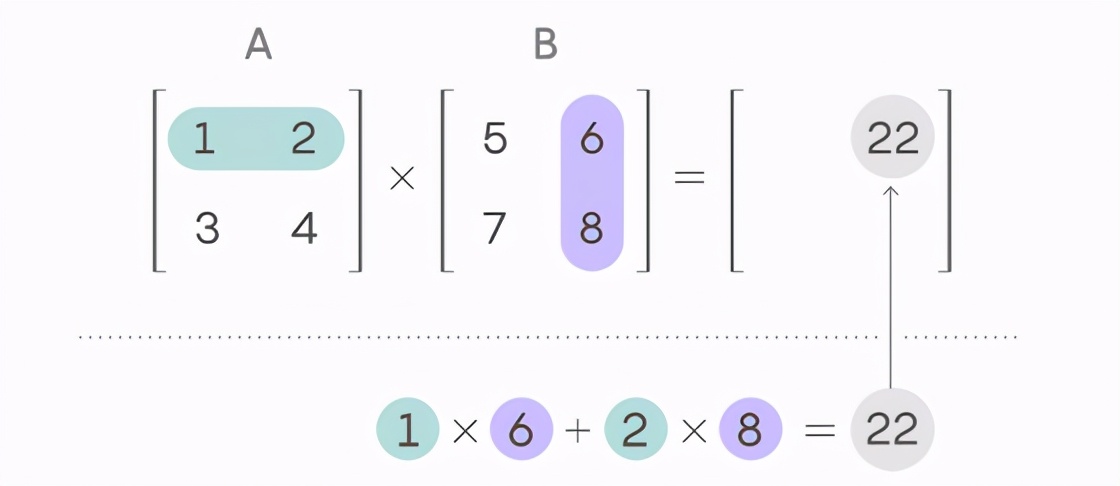
上述運算被稱為矩陣的內(nèi)積（inner product），按照上圖所示的方法可以計算乘積矩陣中其他元素的值。對于上圖的情況，這樣的方法需要進(jìn)行 8 次乘法運算，還有一些加法運算。通常，兩個 n x n 矩陣相乘，一共需要 n^3 次乘法運算。

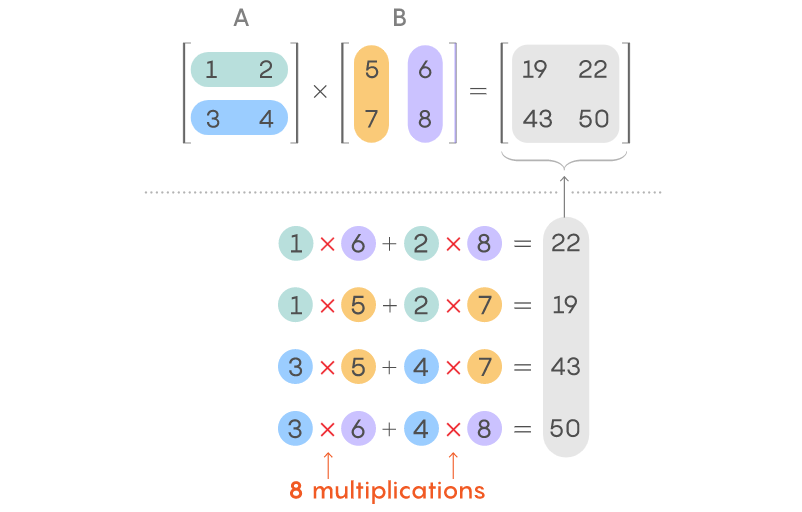
隨著矩陣的增大，矩陣乘法所需的乘法運算數(shù)量比加法運算漲得快得多。通常，研究人員僅根據(jù)所需的乘法次數(shù)來度量矩陣乘法的運算速度。

幾個世紀(jì)以來，人們一直認(rèn)為 n^3 就是完成矩陣乘法最快的速度。Strassen 提出了一組復(fù)雜的關(guān)系，從而利用 14 次加法替換了上述 8 個乘法之一。

1981 年，Arnold Schönhage 利用這種方法證明了矩陣乘法的計算復(fù)雜度可以降低至 O(n^2.522)，Strassen 后來將此方法稱為 laser 方法。

創(chuàng)造新紀(jì)錄

幾十年以來，矩陣乘法運算的每次提速都得益于 laser 方法的改進(jìn)，原因是研究者們找到了在這兩類問題之間進(jìn)行轉(zhuǎn)換的高效方法。Alman 和 Vassilevska Williams 的新方法也是如此。

矩陣乘法中，兩個 n x n 矩陣的計算復(fù)雜度可以用

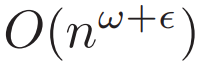
表示，其中

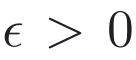
此前最快的紀(jì)錄是 2014 年 François Le Gall 創(chuàng)造的，其中：

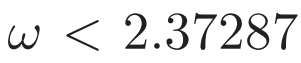
而在 Alman 和 Vassilevska Williams 的新方法中：

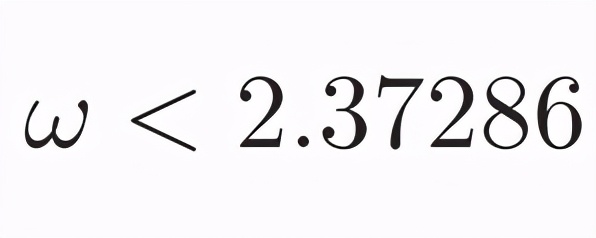
具體地講，他們將復(fù)雜度降至了 O(n^2.3728596)，創(chuàng)造了矩陣乘法運算最快的新紀(jì)錄。

值得一提的是，2012 年 Vassilevska Williams 就曾將這一數(shù)字降至 n^2.372873，不過在 2014 年被 François Le Gall 的 n^2.3728639 打破了。

然而，盡管這種方法為矩陣乘法的速度帶來了一定的改進(jìn)，但可以看到，改進(jìn)的幅度越來越小。

實際上，Alman 和 Vassilevska Williams 的改進(jìn)可能已經(jīng)達(dá)到了 laser 方法的極限，但仍與終極理論目標(biāo)相去甚遠(yuǎn)。

加州理工學(xué)院計算機科學(xué)教授 Chris Umans 表示：「使用該研究中的方法不太可能將復(fù)雜度降至 O(n^2)」。若想達(dá)到，還需找到新的方法。