矩陣乘法無需相乘,速度提升100倍,MIT開源最新近似算法
本文經AI新媒體量子位(公眾號ID:QbitAI)授權轉載,轉載請聯系出處。
在不做乘加操作(multiply-adds)的情況下,能計算矩陣乘法嗎?
矩陣乘法包含大量a+b×c類運算,因此常在運算中將乘法器和加法器進行結合成一個計算單元,進行乘法累加操作。
用近似算法的話,確實可以!
這是來自MIT的最新研究,他們提出了一種新的近似算法MADDNESS,在確保一定精度的情況下,將速度提升到了現有近似算法的10倍,比精確算法速度快100倍,被ICML 2021收錄。

研究還認為,新算法可能比最近大火的稀疏化、因子化等操作更有前途。
目前,作者已經開源了算法代碼,感興趣的小伙伴們可以去嘗試一下。
一起來看看。
用K聚類算法搞個查找表
這個算法,借鑒了一種叫做乘積量化(Product Quantization)的方法。
其中,量化本質上是一種近似操作。
由于矩陣乘法中的每個元素,都可以看做是兩個向量的點積,因此可以通過查找相似向量,來近似地估計向量的點積,而無需再進行大量乘法運算。
乘積量化的具體原理如下:
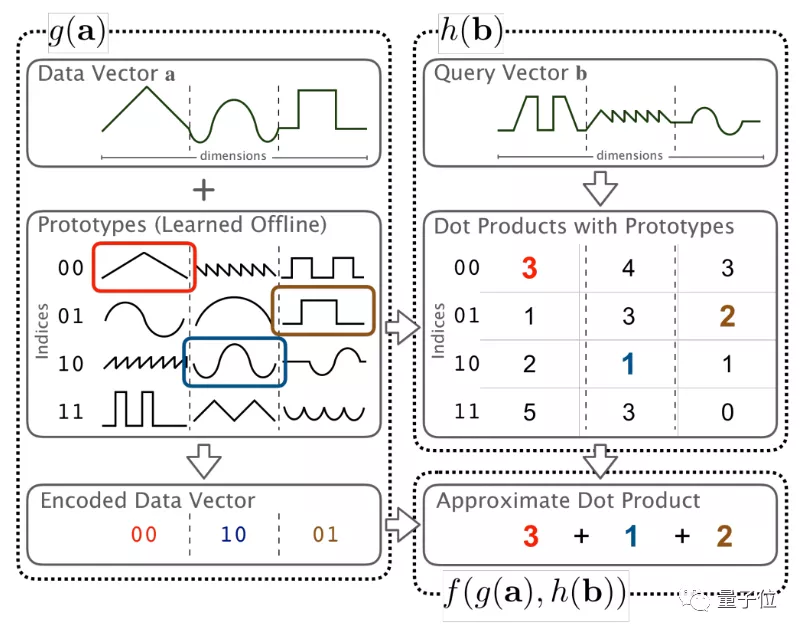
當我們輸入一個要計算的向量a的時候,函數g(·)會對a進行一個近似操作,從一個提前設置好的數值查找表中,找到與它最相近的那個值,并輸出一個近似的向量g(a)。
與此同時,這張表格中的每個值,都已經提前做過點積計算了,因此在輸出g(a)的同時,它與查詢向量(query vector)b對應的近似點積計算結果h(b)也能被查表并輸出。
最后,只需要用f(·,·)函數對g(a)和h(b)做加法運算,而不需要再做乘法計算了。
簡單來說,就是通過近似查表的方法,節省了矩陣乘法中的乘法計算時間。
那么,這樣的數值查找表,究竟要設置什么數值,才能確保在近似計算過程中,損失的計算精度最小呢?
這里借鑒了一下K聚類算法(K-means)的思路,即將數據預分為K組,隨機選取K個對象作為初始聚類中心,再通過訓練迭代,確保在將樣本分到K個類中時,每個樣本與其所屬類中心的距離之和最小。
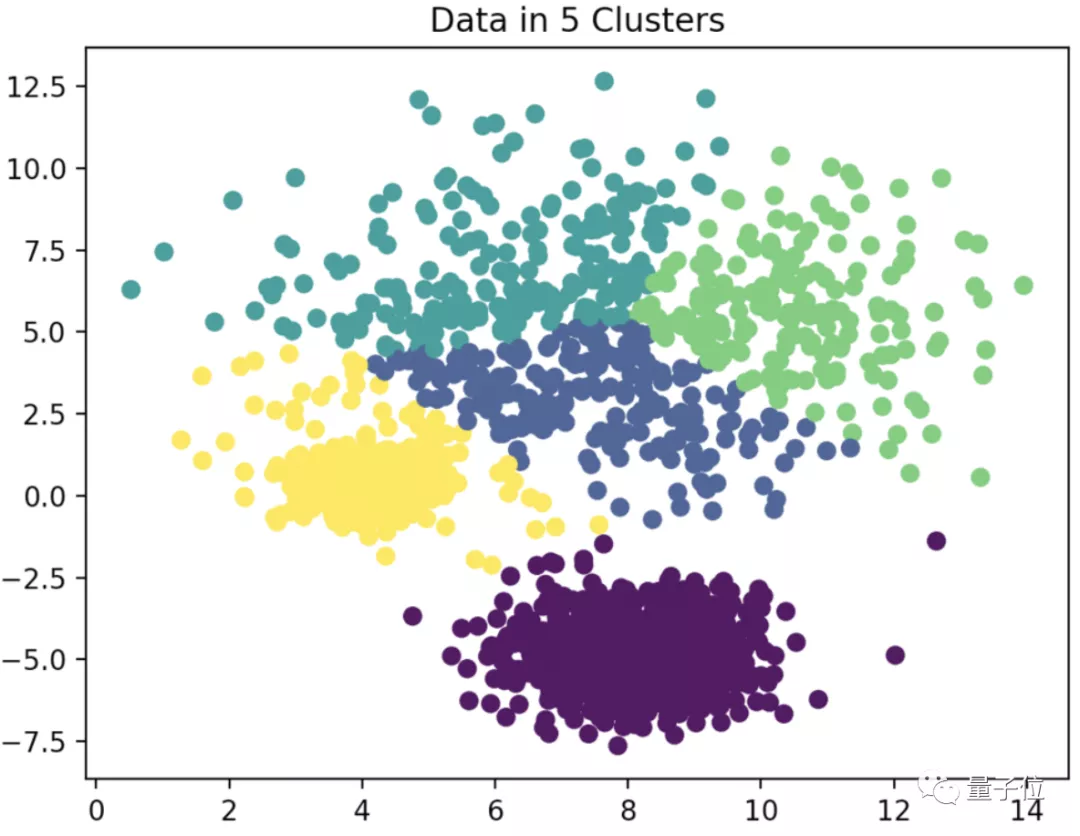
△可視化的K聚類算法
通過這種方法計算出來的數值查找表,能更準確地近似矩陣乘法的數值計算結果。
根據這樣的思路,作者們提出了一種高效的向量乘積量化函數,能在單CPU中每秒編碼超過100GB的數據;同時,還提出了一種針對低位寬整數的高速求和函數。
然后,基于這兩類函數,整出了一套全新的矩陣乘法算法MADDNESS。
這個近似算法的效果如何呢?
精度保持,效率提升數倍
這個算法所需要的算力并不高,在搭載英特爾酷睿i7-4960HQ(2.6GHz)處理器的Macbook Pro上就能完成。
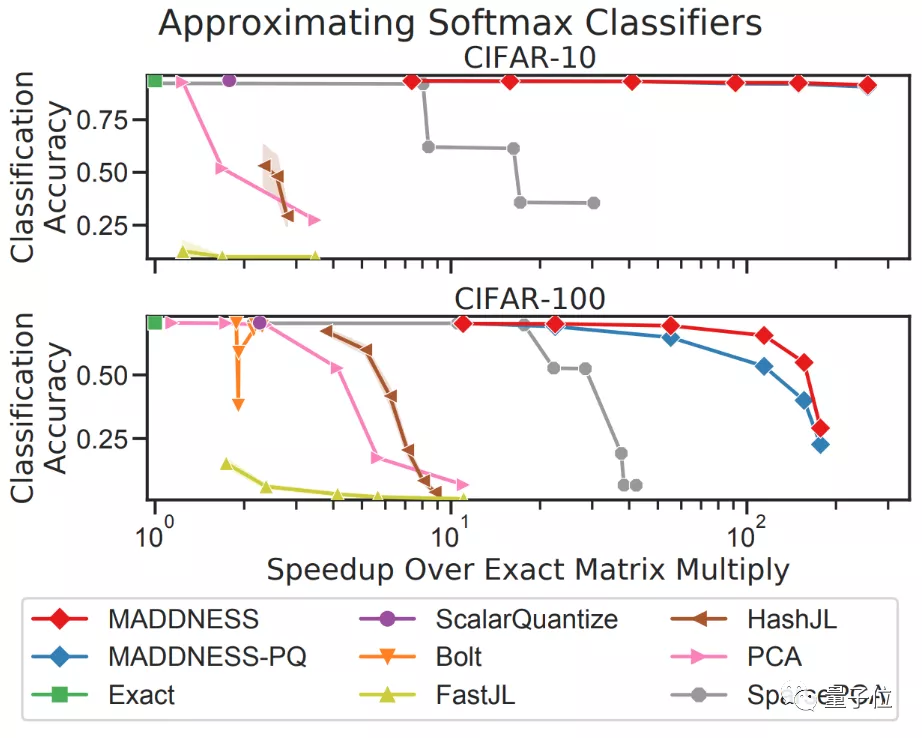
他們在Keras版本的VGG16模型上進行了測試,所用的數據集是CIFAR-10/100,對一系列最新的近似算法進行了評估:
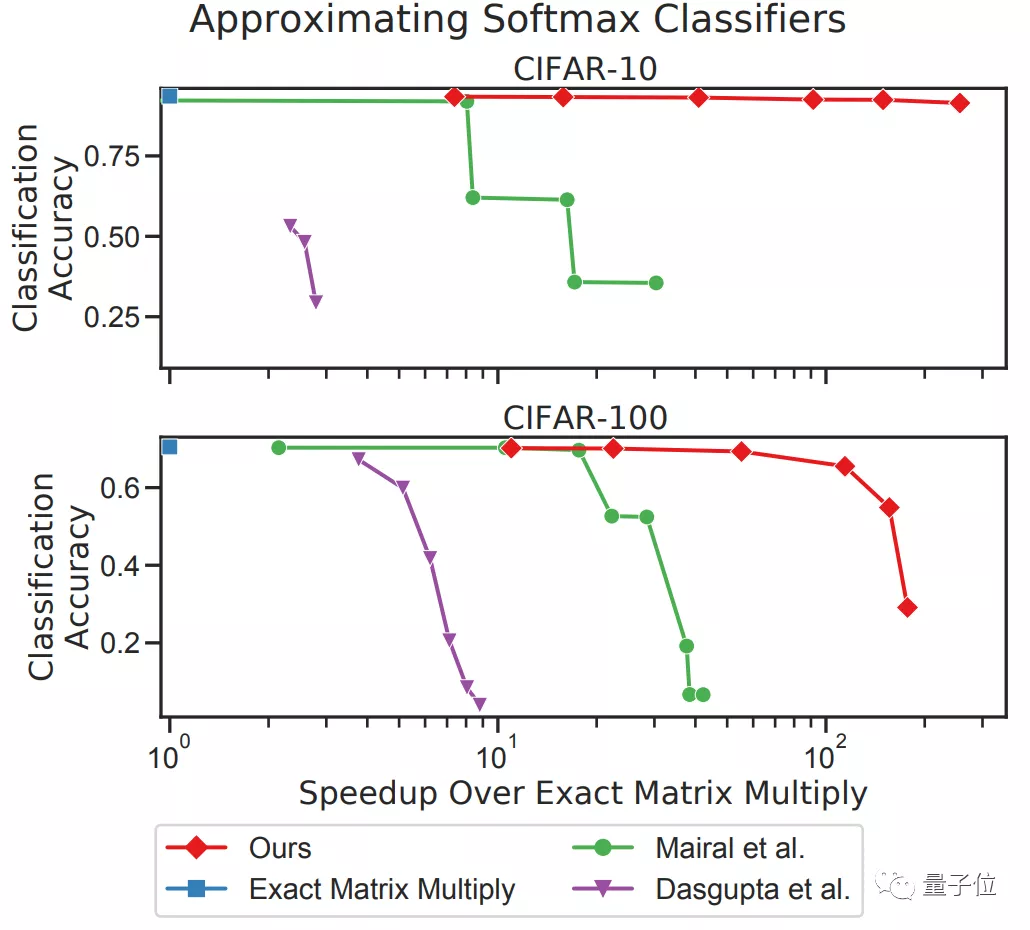
從圖中來看,在效率提升接近10倍的情況下,采用MADDNESS(圖中紅線)仍然能在CIFAR-10上保持幾乎不變的精度。
即使是在CIFAR-100上,在精度幾乎不變的情況下,MADDNESS和MADDNESS-PQ也同樣實現了效率最大化的結果。
除了最新算法外,與其他的現有算法相比(包括作者們在2017年提出的Bolt算法),效果同樣非常拔尖。
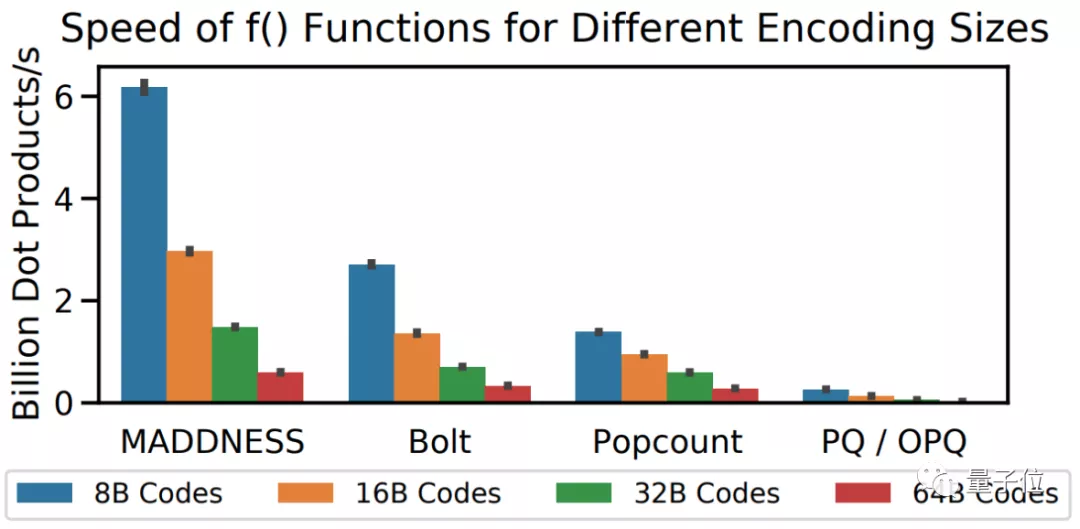
對比計算速度的話,MADDNESS的點積速度就能比現有最快方法快兩倍左右。
當然,也有讀者指出,這篇論文還存在一些待解決的問題:
①論文用的是VGG16模型,但沒有在Transformer等更經典的模型(如BERT)中進行實驗;②雖然對矩陣乘法進行了加速,但畢竟只是近似算法,意味著潛在的精度損失;③沒有在GPU中測試評估結果。

但他仍然認為,這不失為一篇非常有意思的研究。
作者介紹
Davis Blalock,MIT的計算機系博士生,致力于研發快速機器學習算法,他認為速度是衡量機器學習模型的一個非常重要的因素。
John Guttag,MIT計算機系教授,研究方向是機器學習、AI和計算機視覺,目前的研究項目集中在醫療AI和醫學成像上。
值得一提的是,這兩位研究人員,此前還炮轟過神經網絡中的剪枝算法。

他們針對其中的81種算法進行了橫向對比,發現“沒有明確證據表明,這些算法在10年內,對任務效果有明顯改善”。
研究一作Davis Blalock還認為:
這些改進都是所謂的“微調”,而不是科研人員聲稱的“核心創新”,甚至有些改進方法可能根本就不存在。
在對AI模型進行效率提升上,兩位作者確實是很嚴格了。
項目地址:
https://github.com/dblalock/bolt
論文地址:
https://arxiv.org/abs/2106.10860