一枚「棄子」打破80年黎曼猜想紀錄!菲爾茲獎得主MIT大拿聯手,陶哲軒轉贊
「千禧年七大數學難題」之一——黎曼猜想(Riemann hypothesis,RH)取得了顯著突破,數學家們距離摘取「猜想界的皇冠」又近了一步!
MIT對黎曼猜想的潛在例外情況,提出了更加嚴格的限制,此舉直接打破了80多年的紀錄。

論文地址:https://arxiv.org/abs/2405.20552
如今,黎曼猜想依舊是數學中最重要的未解之謎之一。如果能夠證明它,數學家將對素數的分布有更深刻的理解,
并且,很多數論和復變函數領域的工作都基于黎曼猜想為真這個前提,因此一旦證明了黎曼猜想,許多其他工作也會得到完整的證明。

解決黎曼猜想的人,將會獲得克雷數學研究所提供的100萬美元獎勵。
目前,對于如何證明黎曼猜想,數學家們還無從下手,不過他們仍然可以通過證明可能的例外數量有限,來獲得有用的結果。
在今年5月,Maynard和MIT的Larry Guth確定了一種特定類型例外數量的新上限,打破了此前80多年的紀錄。
憑借新的證明,他們得到了數軸上短區間內素數數量的一個更好的近似值,并且有望提供更多關于素數行文的見解。
離完全解決黎曼猜想還遠,但仍然是歷史性的時刻
羅格斯大學的Henryk Iwaniec對此評論道:「這是一個轟動性的結果,這個過程非常非常難,但他們摘下了寶石。」
陶哲軒對這篇論文大加贊賞:
Guth和Maynard對黎曼假設有了顯著的突破,對1940年關于黎曼zeta函數零點的經典Ingham界限進行了第一次實質性改進(更廣泛地說,控制各種狄利克雷級數的大值)。
他認為這是歷史性的時刻,「在黎曼猜想存在之后的八十年里,對這一約束的唯一推動就是對??(1)誤差的微小改進」。
盡管他也承認,「離完全解決這個猜想還很遠」。

要知道,早在2008年,美國楊百翰大學的數學家Xian-Jin Li也曾在arxiv上發表過一篇論文,宣稱證明了黎曼猜想。后被陶哲軒和法國數學家Alain Connes(均為菲爾茲獎得主)無情地指出了Li證明過程中的錯誤。
那么,這次Guth和Maynard的研究能得到陶哲軒的轉發,可見其意義非凡了。
巧妙的迂回
黎曼猜想涉及數論中的一個核心公式——黎曼ζ函數。ζ函數是簡單求和的推廣形式:
1 + 1/2 + 1/3 + 1/4 + 1/5 + ?
這個級數隨著項數的增加會變得無限大,這個過程被數學家稱之為「發散」。但如果改為求和:
1 + 1/2^2 + 1/3^2 + 1/4^2 + 1/5^2 + ? = 1 + 1/4 + 1/9 + 1/16 + 1/25 + ?
我們就會得到π^2/6,大約等于1.64。
而黎曼做出了一個出人意料的偉大構想,將這樣的級數變成一個如下所示的函數:
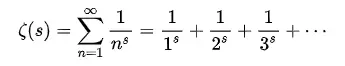
所以 ζ(1) 是無窮大,但 ζ(2) = π^2/6。

當我們將s設為一個復數時,事情變得非常有趣。
復數有兩個部分:「實部」,即日常生活中的數字,以及「虛部」,即日常數字乘以-1的平方根(數學家將其記作i)。
復數可以在平面上繪制,實部在x軸上,虛部在y軸上。例如,3 + 4i。
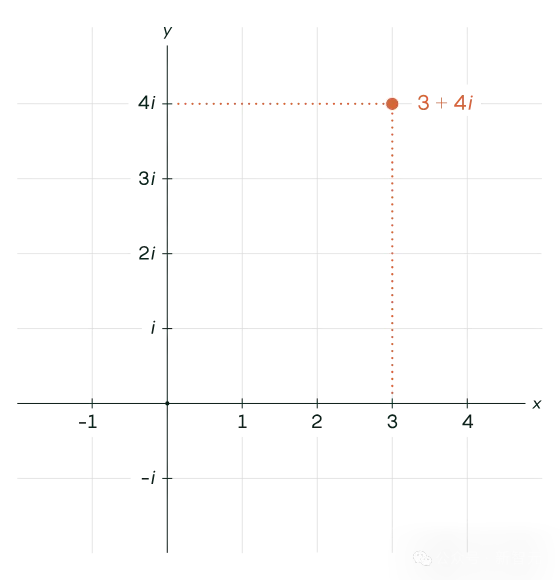
ζ函數以復平面上的點作為輸入,并輸出其他復數。
事實證明,對于某些復數,ζ函數的值為零。確定這些零點在復平面上的具體位置,是數學中最有趣的問題之一。
1859年,黎曼猜測:所有的零點都集中在兩條線上。如果我們擴展ζ函數,使其可以處理負數輸入,我們就會發現對于所有負偶數:-2, -4, -6等等,ζ函數的值為零。
這相對容易證明,因此這些被稱為平凡零點。
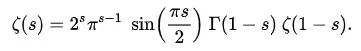
當s的實部小于1時,整個級數和可能會發散。為了讓函數適用于更廣的范圍,黎曼把上面的ζ函數改寫成以上形式
Riemann猜測該函數的所有其他零點(也即非平凡零點)的實部都為1/2,因此位于這條垂直線上。
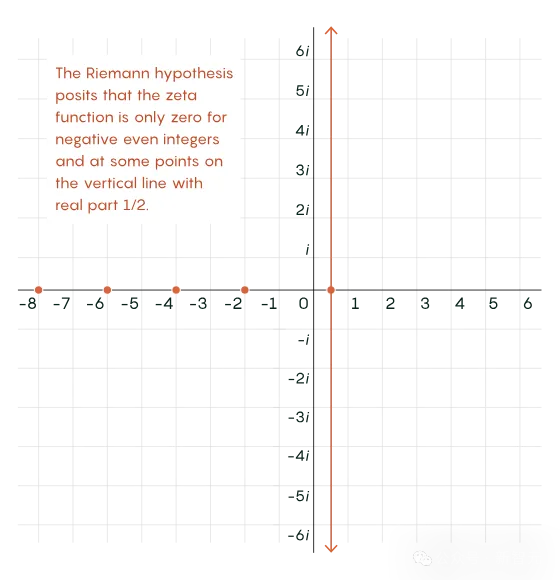
這是黎曼猜想,證明它一直極其困難。
數學家們知道,每個非平凡零點的實部必須在零和1之間,但他們無法排除有些零點的實部可能是0.499。
他們能做的是,就是證明這樣的零點必須非常罕見。

更直觀地說,根據ζ函數能夠畫出無窮多個點。黎曼猜測,這些點有一定的排列規律,一部分在一條橫線上,另一部分則在一條豎線上,所有這些點都在這兩條直線上排列,無一例外
在上圖中,由于有無窮多個點,所以不能用枚舉法證明所有的點都在這兩條線上,因為永遠也驗證不完。但只要有一個點不在這兩條直線上,那就能推翻黎曼猜想。

數學家們已經使用計算機驗證了最初的1億億個點,全都符合黎曼猜想的排列規律。

許多年來,許多數學家為了證明這個猜想前赴后繼,但無一人能夠捧回這個「數學界的圣杯」,甚至不乏有數學家為此而抱憾離世,將無盡的思考留給了后人。
美國數學家Hugh Montgomery甚至表示,如果有魔鬼答應讓數學家們用自己的靈魂來換取一個數學命題的證明,大多數學家想要換取的將會是黎曼猜想的證明。
80多年的紀錄,忽然被打破了
1940年,一位名叫Albert Ingham的英國數學家建立了一個上限,用于估計實部不等于1/2的零點數量,這個上限,至今仍被數學家們用作參考點。

幾十年后,在1960年代和70年代,其他數學家找到了將Ingham的結果轉換為關于素數在數軸上如何聚集或分散,以及它們可能形成的其他模式的描述方法。
大約在同一時間,數學家們還引入了新的技術,改進了Ingham對實部大于3/4的零點的上限。
但事實證明,最重要的零點,就是那些實部正好為3/4的零點。
「許多關于素數的重要結果,都受限于我們對實部為3/4的零點的理解,」Maynard說。
James Maynard是數學領域的杰出學者,曾于2022年獲得菲爾茲獎。
他本科畢業于劍橋大學,博士畢業于牛津大學,從2018年起任教于牛津大學數學研究所。

大約十年前,Maynard就開始思考,如何改進Ingham對這些特定零點的估計。「這是我在解析數論中最喜歡的問題之一。總覺得只要再努力一點,就能取得進展。」
但年復一年,每當他想要解決這個問題,總會被卡住。
然后,在2020年初,在飛往科羅拉多參加會議的飛機上,他突然有了一個想法——或許調和分析中的工具可能會有用。

巧的是,MIT的一位調和分析專家Larry Guth,恰好也參加了同一個會議。
碰巧在思考類似問題的兩個人,就這樣相遇了。
不過,Guth對解析數論完全不熟悉。在午餐時間,Maynard向他解釋了數論方面的內容,還給了他一個具體的測試案例。

斷斷續續研究了幾年后,Guth才意識到,他的調和分析技術行不通。
但他并沒有停止思考這個問題,而是嘗試了新的方法。
今年二月份,他再次聯系了Maynard。結合不同的視角,兩人開始認真合作。
幾個月后,他們得出了結果。
數學中的「棄子」
Guth和Maynard首先將他們想要解決的問題轉換成另一種形式。
如果某個零點的實部不是1/2,那么被稱為狄利克雷多項式的相關函數,必須產生一個非常大的值。
因此,證明黎曼猜想的例外很少等同于證明狄利克雷多項式不會經常產生很大的值。
然后,數學家們進行了另一種轉換。
首先,他們使用狄利克雷多項式構建了一個矩陣,或者說一個數字表。
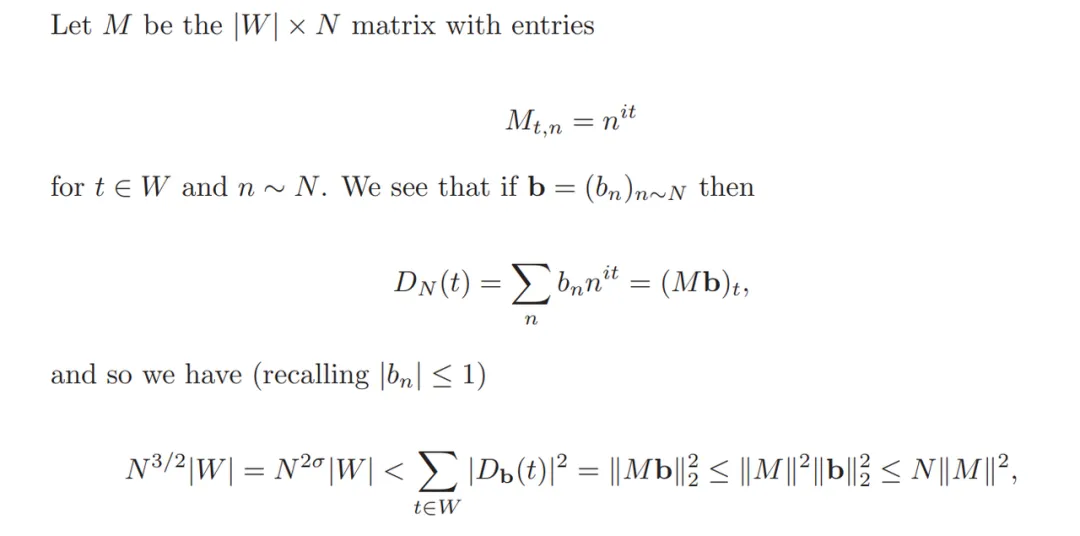
「數學家們喜歡看到矩陣,因為矩陣是我們非常了解的東西,」Guth說。「你要學會保持敏銳的嗅覺,準備好看到矩陣無處不在。」
矩陣可以「作用于」一個叫做向量的數學對象,向量由長度和方向定義,從而產生另一個向量。
通常情況下,當矩陣作用于向量時,會改變向量的長度和方向。
有時會有一些特殊的向量,當它們經過矩陣時,只改變長度而不改變方向。這些向量稱為特征向量。
數學家們用稱為特征值的數字,來衡量這些變化的大小。
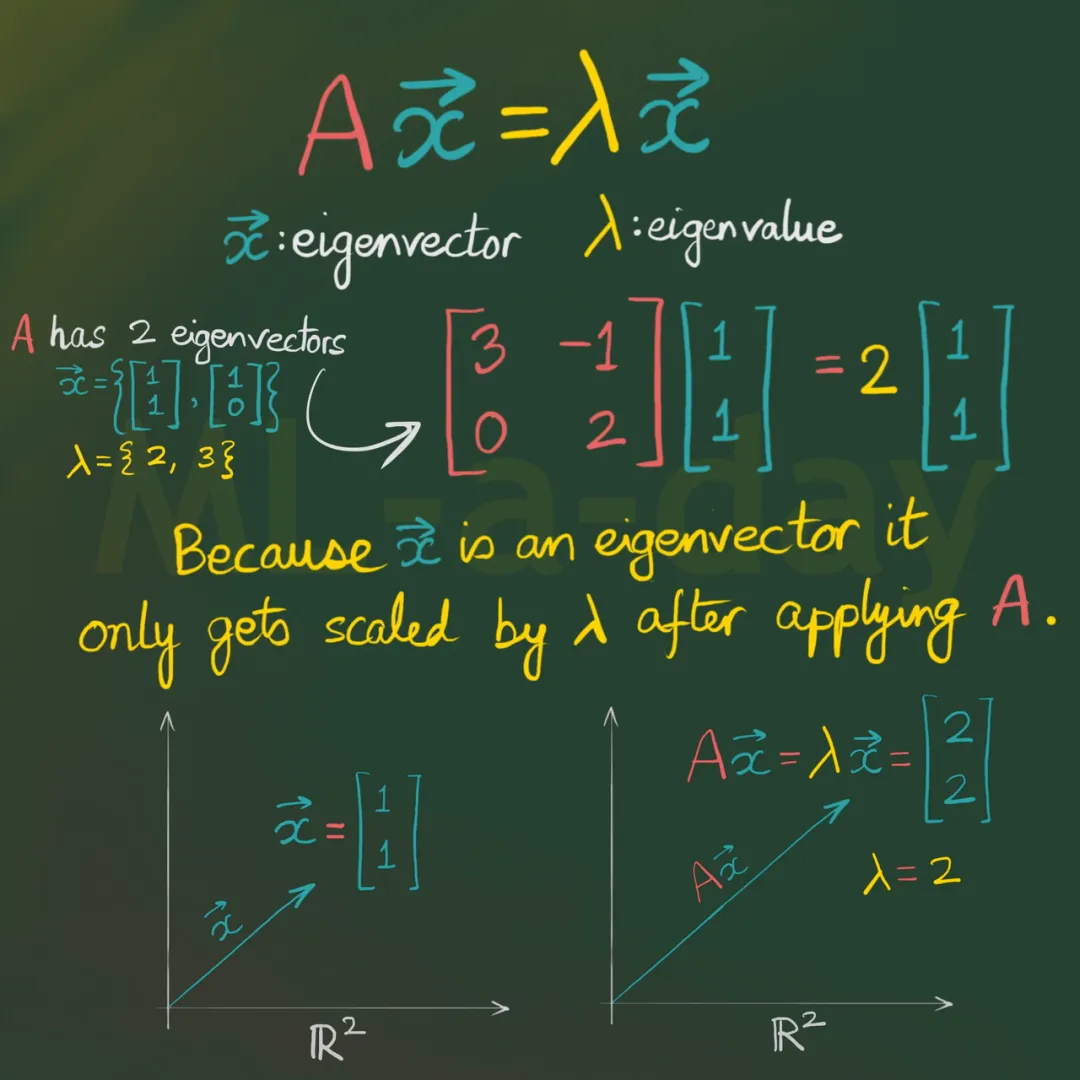
Guth和Maynard重新表述了他們的問題,使其變成了關于矩陣最大特征值的問題。
如果他們能證明最大特征值不能變得太大,他們的工作就完成了。
為此,他們使用了一個公式,得到了一個復雜的總和,并尋找方法使總和中的正負值盡可能地相互抵消。
「你必須重新排列序列,或者從正確的角度看它,以看到某種對稱性,從而實現一些抵消,」Guth說。

這個過程涉及幾個令人驚訝的步驟,其中一個最重要的想法,被Maynard形容為「有點神奇」。
在某個時刻,他們本應采取一個看似顯而易見的簡化步驟,來簡化他們的總和。
然而他們并沒有這樣做。反之,他們把總和保留在更長、更復雜的形式。
「我們做了一些乍一看完全愚蠢的事情,我們就是拒絕做標準的簡化,」Maynard說。「我們放棄了很多,這意味著現在我們不能為這個總和得到任何簡單的界限。」
但從長遠來看,這證明是一個有利的舉動。
「在國際象棋中,這被稱之為棄子——為了在棋盤上獲得更好的位置而去犧牲一枚棋子,」Maynard說。

而Guth將其比作玩魔方:有時你必須撤銷之前的動作,使一切看起來更糟,然后找到一種方法,讓更多的顏色到達正確的位置。

「我們需要極大的勇氣,才能拋棄一個顯而易見的改進,然后希望自己能在之后恢復它,」牛津大學的數學家、Maynard的前導師Roger Heath-Brown說。「這與我認為應該做的一切背道而馳。」
但這位導師承認,這恰恰是自己卡住的地方。
Maynard說,Guth作為一個調和分析專家而不是數論學家,使得這一策略成為可能。「他沒有被這些固有的規則所禁錮,所以他更愿意考慮那些不合常規的事情。」
最終,他們能夠對最大特征值設定一個足夠好的界限,這又進一步轉化為對黎曼猜想潛在反例數量的更精確界限。

盡管他們的工作始于啟發了Guth的調和分析思想,但他們最終卻將這些復雜技術排除在外,返璞歸真。
「現在看起來,這就像是我40年前可能會嘗試的事情,」Heath-Brown說。
最終,通過給出對實部為3/4的零點數量的更好界限,Guth和Maynard自動證明了一些關于素數分布的結果。
例如,對于較短區間,估計在給定區間內找到的素數數量會變得不那么準確。而新的工作,能使數學家們在更短的區間內得到良好的估計。
數學家們認為,這個證明還可能改進其他關于素數的結論。
并且,Guth和Maynard的技術似乎還有余地進一步改進。
不過Maynard認為,這些技術不是解決黎曼猜想本身的正確方法。
「它還需要來自其他地方的一些重大想法。」
陶哲軒解讀:利用解析數論意想不到的方式
對于這個「棄子」的方法,陶哲軒也給出了更專業的解讀——
如果令??(σ,??)表示實部至少為σ、虛部至多為??的黎曼zeta函數的零點數量,黎曼猜想告訴我們,對于任何σ>1/2,??(σ,??)都會消失,當然我們不能無條件地證明這一點。
但下一步,我們可以證明零密度估計,也就是??(σ,??)的非平凡上界。
事實證明,σ=3/4 是一個關鍵值。1940年,Ingham得出了一個結果——??(3/4,??)???^{3/5+??(1)}。
在接下來的八十年里,對該界限的唯一改進是對??(1)誤差的小幅改進。
這限制了我們在解析數論中做很多事情:例如,為了在(??,??+??^??)形式的幾乎所有短區間內得到一個好的素數定理,我們長期以來一直被限制在??>1/6 ,主要障礙是Ingham界限缺乏改進。

Guth和Maynard的最新研究成功改進了Ingham界限,從3/5=0.6降低到13/25=0.52。
這帶來了解析數論的許多相應改進;例如,在幾乎所有短區間內,可以證明的素數定理的范圍從??>1/6=0.166… 變為??>2/15=0.133…(如果黎曼猜想為真,將意味著我們可以覆蓋整個??>0的范圍)。

這些論證本質上主要基于傅立葉分析。前幾步是標準步驟,許多試圖打破Ingham界限的分析數論學家都能認出這些步驟。
但他們有許多巧妙且出乎意料的操作,比如,通過將關鍵的相位矩陣??^{????}=??^{????log???}提升到六次方來控制它(表面上看,這使問題變得更加復雜且棘手)。
以及,拒絕使用駐相法來簡化某個復雜的傅里葉積分,從而在指數上讓步,以保留一種最終證明比駐相近似更有用的因式分解形式;并根據Dirichlet級數大值出現的位置是否具有小、中或大的加法能量來劃分情況,并對每種情況采用稍微不同的論證方法。
在這里,隱含在Dirichlet級數中的相位函數??log???的精確形式變得非常重要;這是利用解析數論中出現的特殊指數和的一種意想不到的方式,而不是在調和分析中可能遇到的更一般的指數和。












































