有了這支矢量神經風格畫筆,無需GAN也可生成精美繪畫
在 CVPR 2021 的一篇論文中,來自網易伏羲和密歇根大學的研究者提出了一種圖像到繪畫的轉換方法,可以生成生動逼真且風格可控的畫作。目前該方法的實現代碼已開源。
論文地址:
https://arxiv.org/abs/2011.08114
Github 地址:
https://github.com/jiupinjia/stylized-neural-painting
不同于此前風格遷移方法在逐像素預測框架下生成繪畫,該方法在矢量空間下生成具有物理意義的序列畫筆參數,且該參數可以進一步用于渲染。由于畫筆本身是不可微的,該研究設計了一種新的神經渲染器,以模擬畫筆的行為,并將畫筆預測問題轉化成參數空間內的搜索問題,從而最大化渲染輸出和輸入圖像之間的相似度。該研究揭示了搜索過程中的零梯度問題并提出從最優搬運的角度解決這一問題。
此外,該研究還揭示了此前神經渲染器存在參數耦合的問題,并重新設計了渲染網絡。新的網絡包含一個柵格化網絡和一個著色網絡,能夠更好地對形狀和顏色解耦合。實驗表明該研究提出的方法在全局和局部紋理層面上具有更高的真實度。另外,該方法還可以在神經風格遷移框架下聯合優化以進一步遷移其他畫作的視覺效果。

圖 1:該研究提出了一種基于畫筆渲染的方法,可以生成逼真的繪畫作品。圖中畫作是在矢量格式下生成的,還可以進一步優化渲染成不同的風格。

生成一幅向日葵畫作。
該研究的主要貢獻包括:
提出一種全新的基于畫筆的圖像到繪畫轉換方法,將畫筆預測問題轉化為參數搜索問題來求解。該方法還可以進一步在神經風格遷移框架下聯合優化以實現風格化效果。
揭示了參數搜索中存在的零梯度問題,并從最優搬運視角來看待畫筆優化問題。該研究引入了可微的搬運損失函數改善畫筆收斂性和繪畫效果。
設計了一種新的神經渲染框架,該框架包含雙通道的渲染管線(柵格化 + 著色)。新的渲染器可以更好地處理畫筆形狀和顏色的解耦合,性能優于此前的神經渲染器。
神經風格畫筆
該研究主要由 3 個功能模塊組成:1)可以根據輸入畫筆參數生成畫筆圖像的神經渲染器;2)可以將多個畫筆組合在一起的可微畫筆混合器;3)用于度量輸入輸出圖像相似度的模塊。
神經風格畫筆解決了藝術繪畫參數化的問題。對于給定的一張空白畫布 h_0,該方法逐步地將畫筆疊加到該畫布上。例如在第 t 步時,一個訓練好的神經渲染器G會將一組畫筆參數X_t 渲染成前景圖像 s_t 和對應的透明度遮罩,然后該方法利用軟混合(soft blending)的方式將當前畫布、新增畫筆、對應遮罩進行疊加并保證整個過程是可微的:
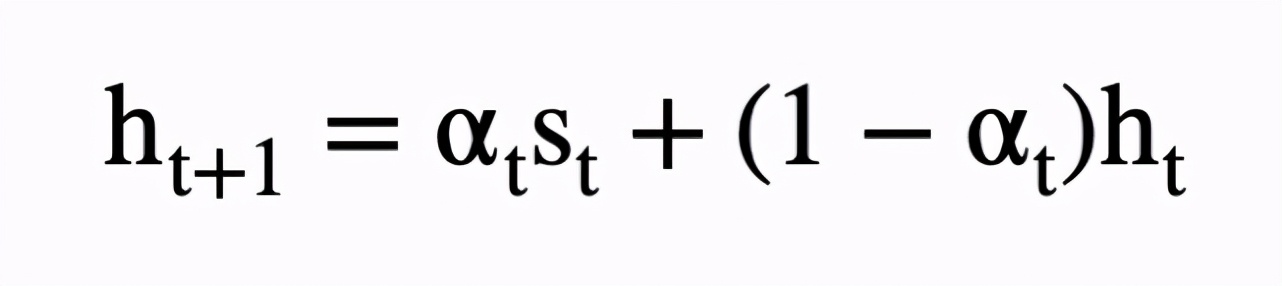
其中。最終該方法將全部T步的畫筆參數收集在一起,并在自監督方式下搜索畫筆參數的最優解,即最終渲染輸出 h_T 需要與輸入圖像盡可能相似:
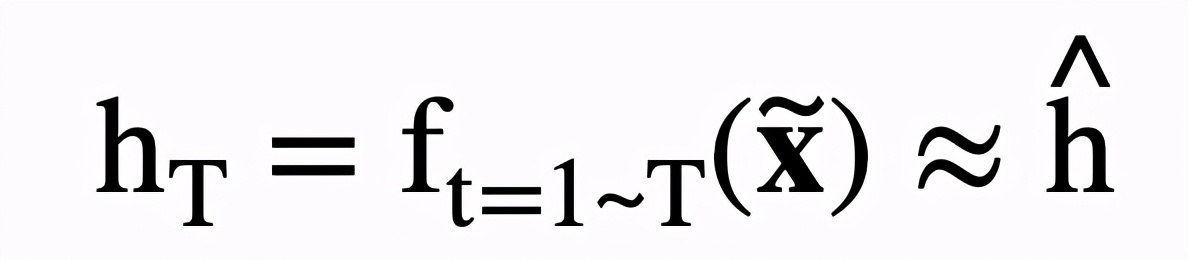
其中表示從畫筆參數到渲染畫布的遞歸映射。表示所有T步的畫筆參數集合。
假定是用于度量畫 h_T 和輸入圖像相似度的損失函數,該方法直接在參數空間內優化所有的輸入畫筆并最小化相似度損失函數,并利用梯度下降來更新畫筆參數:
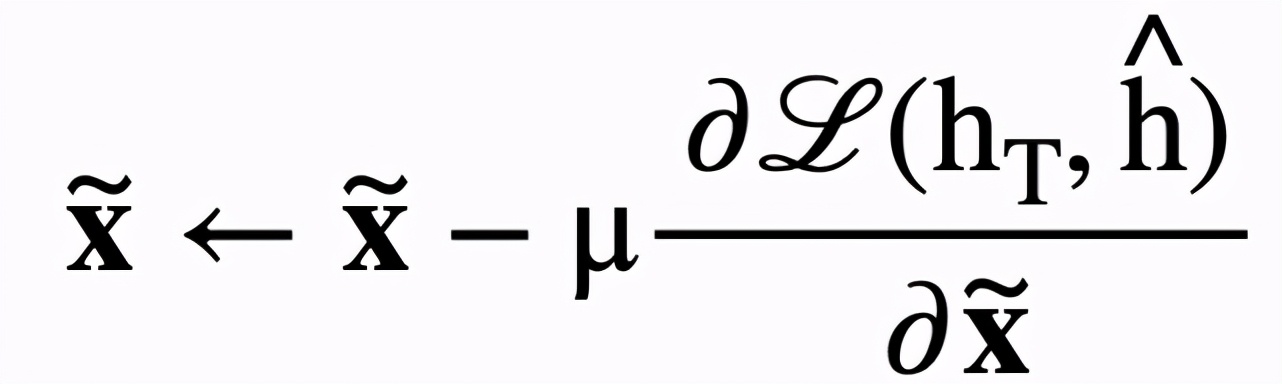
其中是預定義的學習率。
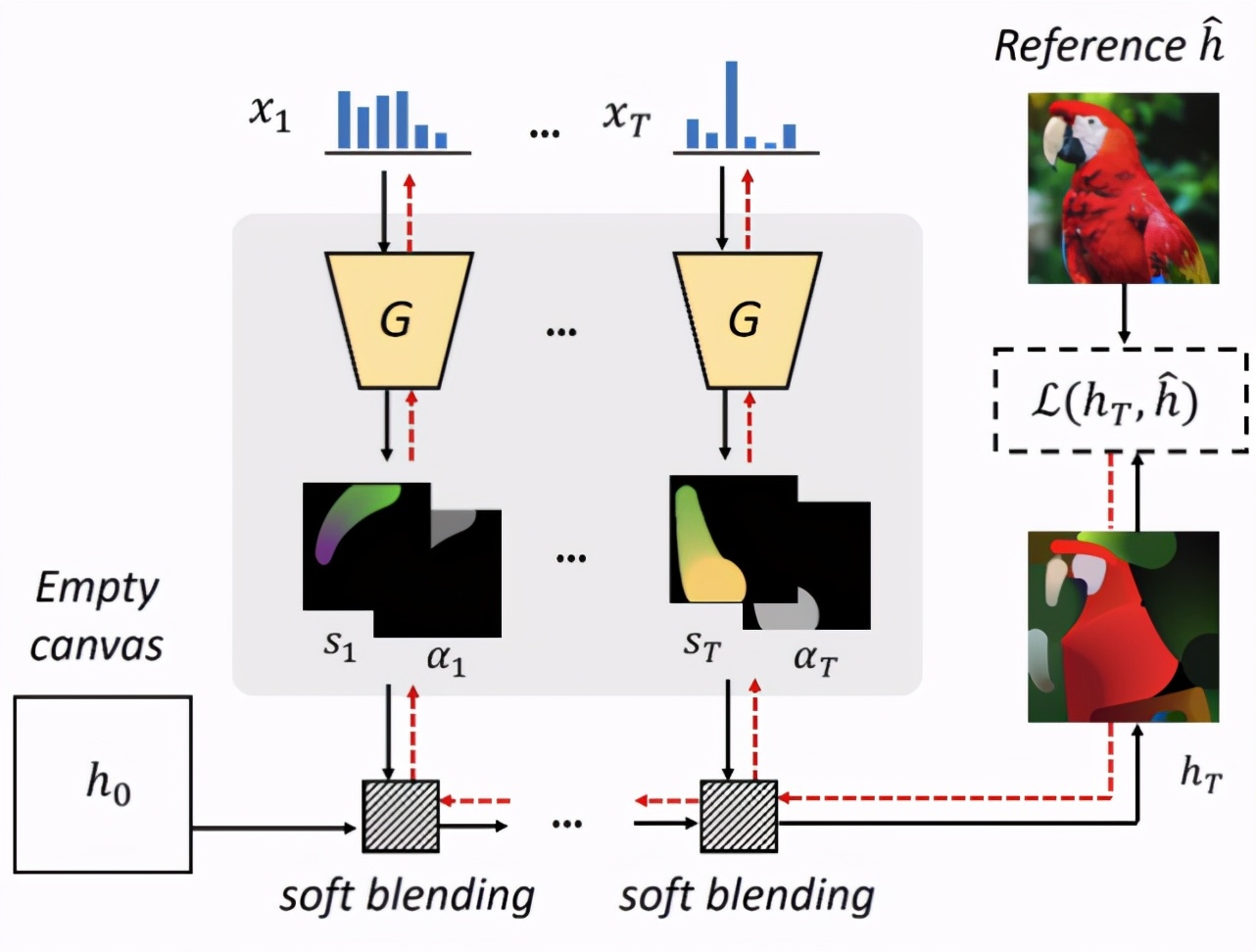
圖 2:該研究從一張空白畫布開始,逐個對畫筆進行渲染,并利用軟混合的方式將畫筆疊加起來。該方法利用梯度下降法來尋找最優的畫筆參數集合,從而使生成的畫作與輸入圖像盡可能相似。圖中黑色箭頭表示前向傳播,紅色箭頭表示梯度反向傳播。
神經渲染器
神經風格畫筆中的核心模塊是神經渲染器。以往的神經渲染器只能夠在比較簡單渲染場景中工作,但當遇到如過渡色和畫筆紋理等更復雜的渲染場景時,上述渲染器將難以很好地表達耦合在一起的畫筆形狀和顏色。該研究借鑒了傳統的渲染管線并設計了一個雙通道的神經渲染器,該渲染器可以很好地解決顏色 / 形狀 / 材質的耦合問題。
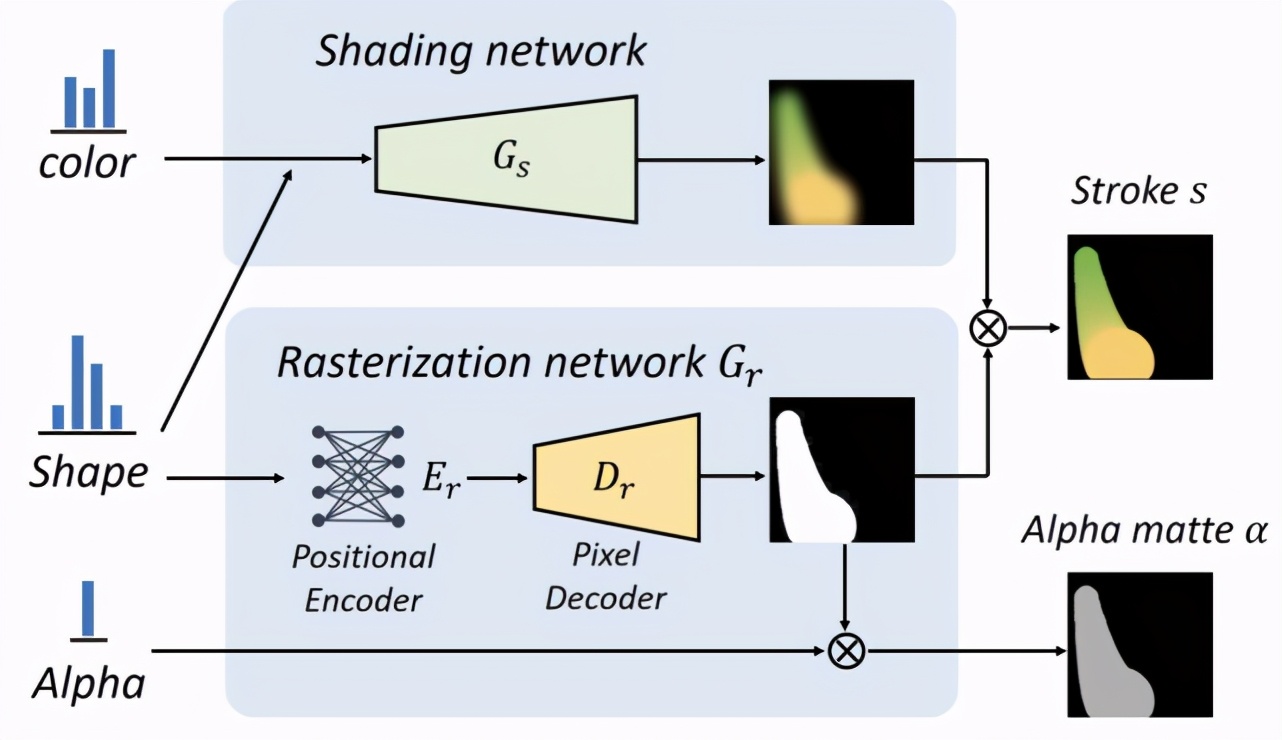
圖 3:該研究設計了一種雙通道神經渲染器,該渲染器由一個著色網絡 G_s 和一個柵格化網絡 G_r 組成,它能夠將輸入的畫筆參數集合渲染成柵格化的前景圖像和對應的透明度遮罩。
新的神經渲染器由兩個子網絡組成:一個著色網絡G_s和一個柵格化網絡 G_r,輸入的畫筆參數X則被分成了三組:顏色、形狀和透明度。著色網絡 G_s由一組堆疊的轉置卷積層(transposed convolution layer)構成,用來將輸入的顏色和形狀參數生成具有可靠前景顏色的畫筆。柵格化網絡 G_r被設計為位置編碼器 + 像素解碼器的形式,它忽略了顏色信息但因此能夠生成具有銳利邊緣的畫筆輪廓。最終,畫筆前景圖像 s 可以根據輪廓圖像對顏色圖像進行掩膜得到,而透明度遮罩則可以利用輸入的透明度對輪廓圖像進行縮放得到。
該研究利用標準的逐像素回歸損失函數對上述渲染器進行訓練:
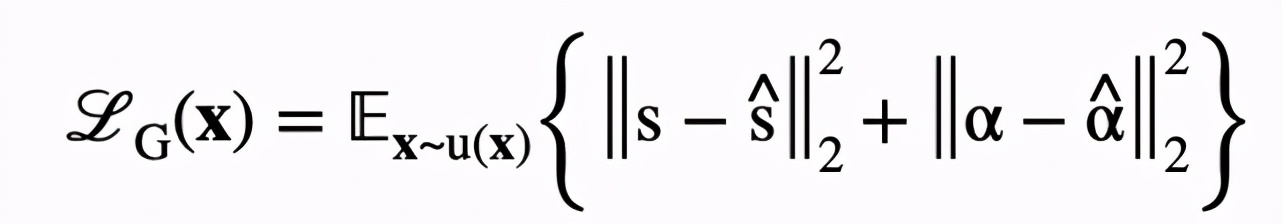
其中和表示利用圖形引擎渲染出的前景圖像和透明度遮罩真值。表示從畫筆參數空間中隨機采樣得到的畫筆參數。
像素相似度和零梯度問題
神經風格畫筆作畫的關鍵在于相似度的定義,例如逐像素的和損失函數就可以直接用于定義渲染結果和輸入圖像之間的相似度。然而神經風格畫筆并非是僅在像素空間中進行優化,而是需要進一步優化畫筆參數,此時逐像素損失函數并非總是能夠保證梯度的有效下降。特別是當渲染的畫筆和其真值不重疊時,就會造成零梯度問題。該研究進一步引入了最優搬運損失函數來解決該問題,如圖 4 和圖 5 所示。
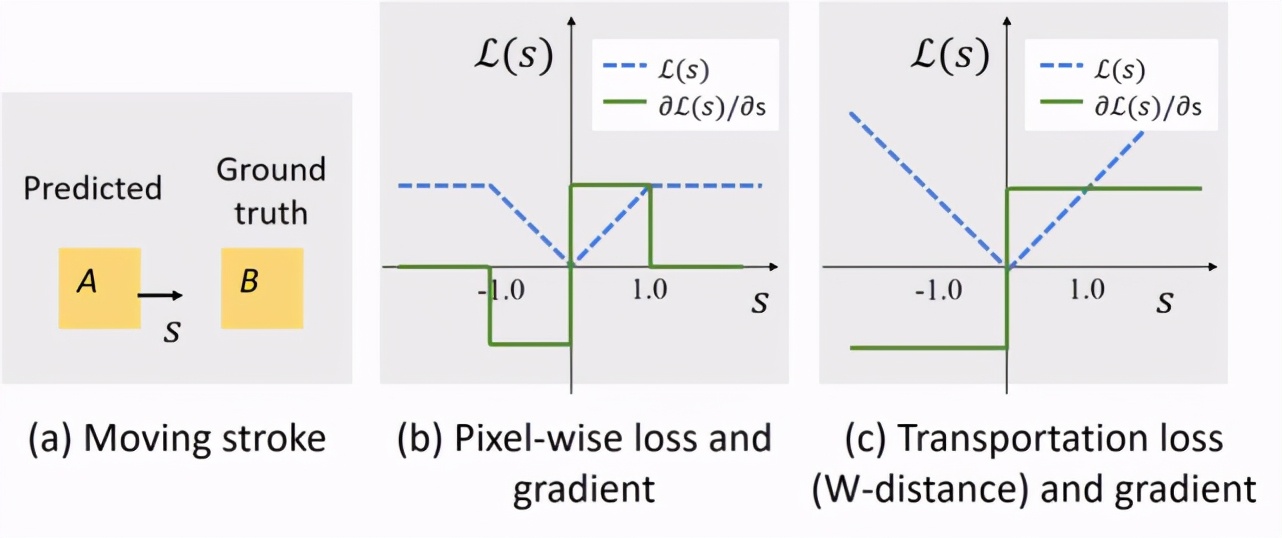
圖 4:一個簡單的實例可以解釋為什么逐像素損失函數在畫筆參數優化時可能存在零梯度問題()。
如圖 4(a)所示,當沿著方向移動一個正方形畫筆A到目標B時,它的逐像素梯度始終為一個常數,特別是當A和B沒有交集時,就會出現零梯度的情況,如圖 4(b)所示。作為對比,如圖 4(c)所示,該研究提出的最優搬運損失函數不存在上述問題,且可以很好地描述A和B之間的物理距離。

圖 5:逐像素損失函數(第一行)和最優搬運損失函數(第二行)在將畫筆從其初始值推向目標位置的對比。
利用最優搬運損失函數,畫筆可以很好地收斂到目標位置,而逐像素損失函數則由于零梯度問題未能收斂。
最優搬運損失函數
該研究定義最小搬運功(即 Wasserstein distance)作為畫布和輸入圖像間的相似度度量。對于給定的畫布 h和輸入圖像,它們的歸一化像素值和被定義為概率邊際函數。表示聯合概率矩陣,其中第(i,j)個元素表示 h 中的第 i 個像素和中的第 j 個像素的聯合概率,n 表示圖像中的像素數目。D表示成本矩陣,其第(i,j)個元素表示 h 中的第 i 個像素和中的第 j 個像素之間的歐氏距離。因此矩陣D列出了從 h 中的一個位置到中的另一個位置移動單位質量所需要消耗的人力成本。在離散的情況下,經典的最優搬運距離可以寫成一個線性優化問題,其中
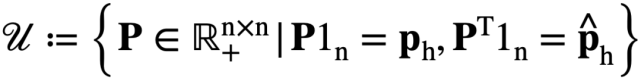
在該研究中,研究者提供了一個經典最優搬運距離的平滑版本,即著名的 Sinkhorn distance。該距離具有良好的數學性質,并且相比于原始的版本能夠大幅度降低計算成本。通過引入拉格朗日乘子和額外的熵約束,上述優化問題可以進一步寫為如下形式:
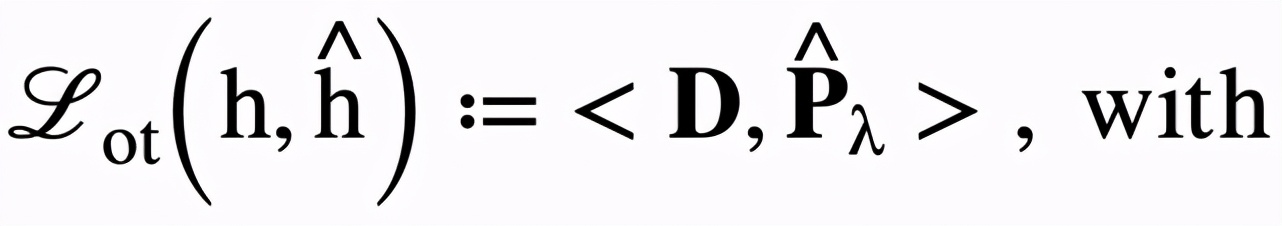
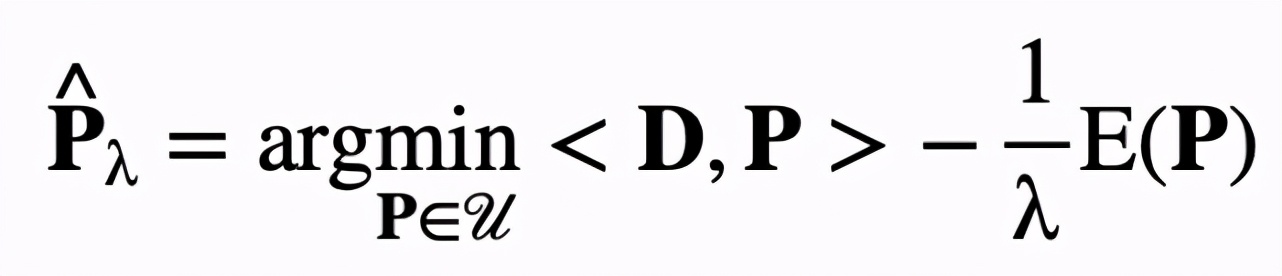
基于上述形式,最優搬運損失函數可以輕易地整合進參數搜索流程并且和其他損失函數聯合優化。因此,神經風格畫筆的總相似度損失函數定義如下:
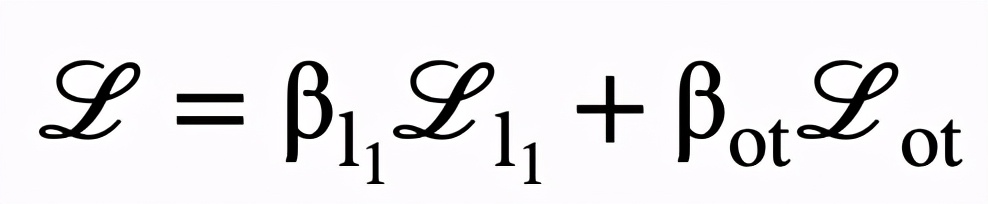
其中用于平衡兩個目標函數。
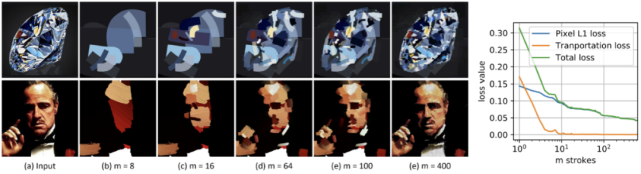
圖 7:上圖展示了逐畫筆的繪畫結果,其中第一行基于馬克筆生成,第二行基于油畫筆生成。右側圖像展示了優化過程中的損失函數曲線。
與神經風格遷移聯合優化
由于神經風格畫筆是在參數搜索范式下實現的,因此該方法天然地適合神經風格遷移框架。由于神經風格遷移被設計為通過更新圖像像素來最小化內容損失函數(content loss)和風格損失函數(style loss),因此研究者進一步將風格損失函數融入神經風格畫筆中,以實現風格化的輸出。擴展后的相似度度量函數可以定義為如下形式:
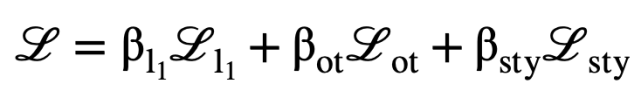
其中為相似度損失函數,該研究中采用與 Gatys 等人相同的形式,即計算基于 VGG-19 所提取特征的 Gram 矩陣。
實驗
風格化繪畫生成實驗
得益于聯合損失函數的設計,神經風格畫筆不僅可以生成逼真的藝術畫作,還可以生成風格化的渲染結果。此外,由于畫筆參數具有明確的物理意義,因此在風格化輸出時還可以進一步控制風格化的范圍(顏色 or 材質)。

圖 8:(a)—(c) 中展示了神經風格畫筆的繪畫結果。(d)中展示了高度抽象的卡通人物畫像。

圖 9:基于神經風格畫筆的風格遷移結果。
對比實驗
此前的繪畫參數化方法主要依靠增強學習來實現,如 “Learning-to-Paint” 算法,而神經風格畫筆通過引入神經渲染器很好地解決了畫筆不可微的問題。因此相比基于 RL 的方法,神經風格畫筆可以生成更加逼真的結果。

圖 10:神經風格畫筆與 Learning-to-Paint 算法對比
除了與此前的方法進行對比,研究者還與人工畫作進行了比較,同樣取得了較好的生成效果。

圖 11:藝術家(Adam Lister)繪畫結果和自動生成的結果
受控實驗
研究者還分別研究了搬運損失函數和雙通道神經渲染器的作用。
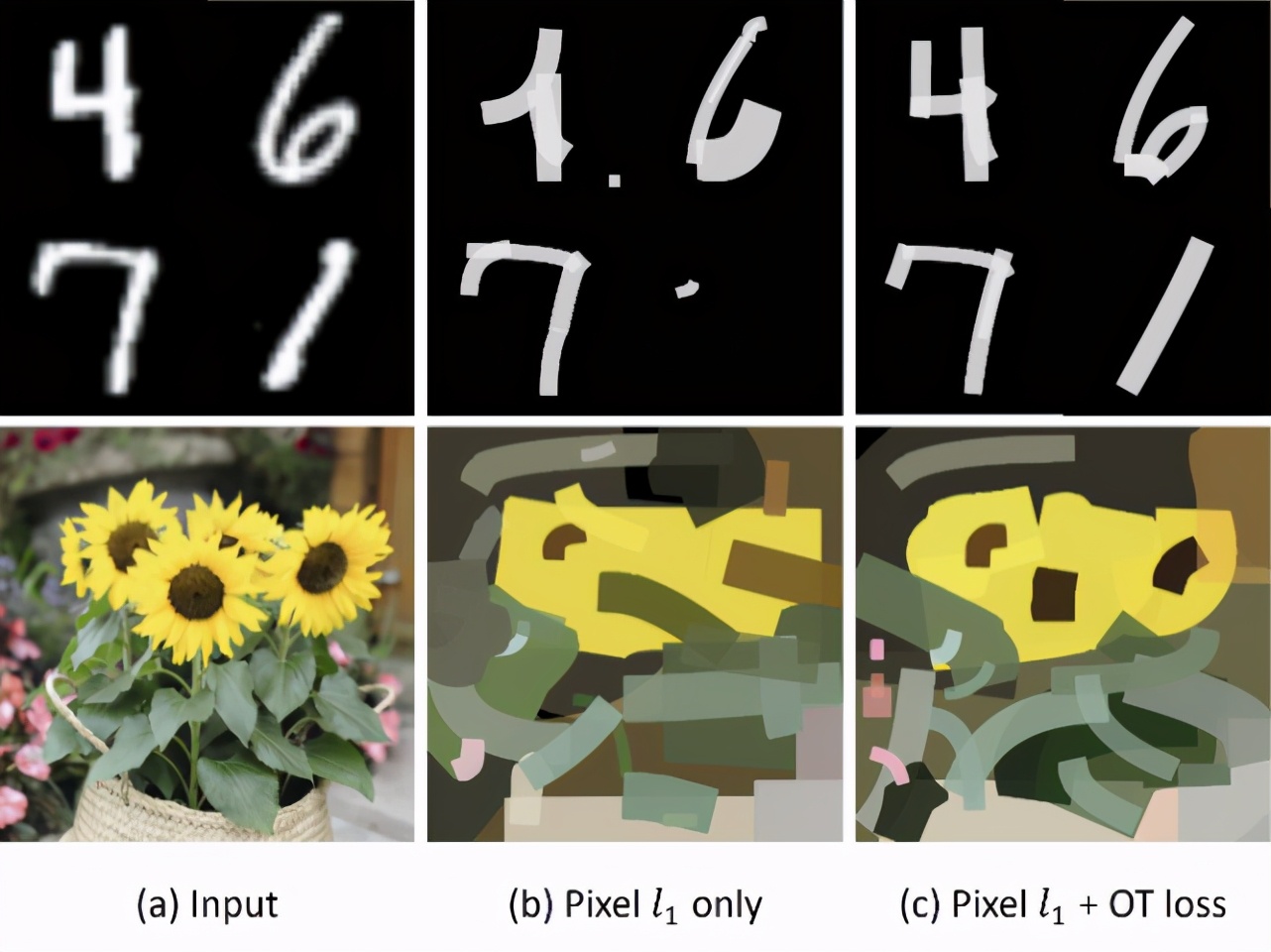
圖 12:使用最優搬運損失函數前后的結果對比。最優搬運損失函數可以有效地恢復圖像中的更多細節,特別是當畫筆初始化的位置與目標區域不重合的時候。
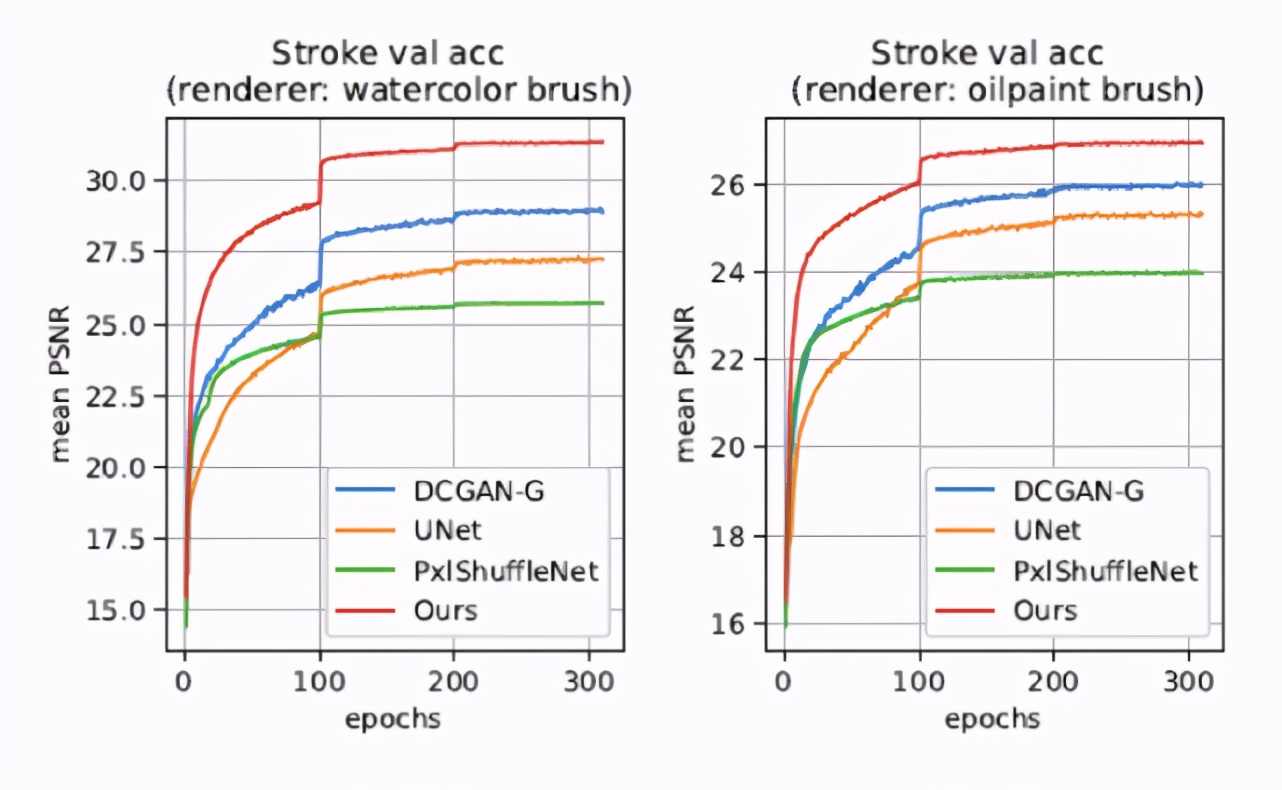
圖 13:不同神經渲染器的驗證集精度(包括 DCGAN-G,UNet,PxlShuffleNet)。該研究提出的雙通道神經渲染器可以有效地提高驗證集精度,并加快收斂速度。

圖 14:不同神經渲染器渲染的可視化結果對比