O(n)的算法居然超時(shí)了,此時(shí)的n究竟是多大?
一些同學(xué)可能對計(jì)算機(jī)運(yùn)行的速度還沒有概念,就是感覺計(jì)算機(jī)運(yùn)行速度應(yīng)該會很快,那么在leetcode上做算法題目的時(shí)候?yàn)槭裁磿瑫r(shí)呢?
計(jì)算機(jī)究竟1s可以執(zhí)行多少次操作呢?接下來探討一下這個(gè)問題。
超時(shí)是怎么回事
大家在leetcode上練習(xí)算法的時(shí)候應(yīng)該都遇到過一種錯(cuò)誤是“超時(shí)”。
也就是說程序運(yùn)行的時(shí)間超過了規(guī)定的時(shí)間,一般OJ(online judge)的超時(shí)時(shí)間就是1s,也就是用例數(shù)據(jù)輸入后最多要1s內(nèi)得到結(jié)果,暫時(shí)還不清楚leetcode的判題規(guī)則,下文為了方便講解,暫定超時(shí)時(shí)間就是1s。
如果寫出了一個(gè)O(n)的算法 ,其實(shí)可以估算出來n是多大的時(shí)候算法的執(zhí)行時(shí)間就會超過1s了。
如果n的規(guī)模已經(jīng)足夠讓O(n)的算法運(yùn)行時(shí)間超過了1s,就應(yīng)該考慮log(n)的解法了。
從硬件配置看計(jì)算機(jī)的性能
計(jì)算機(jī)的運(yùn)算速度主要看CPU的配置,以2015年MacPro為例,CPU配置:2.7 GHz Dual-Core Intel Core i5 。
也就是 2.7 GHz 奔騰雙核,i5處理器,GHz是指什么呢,1Hz = 1/s,1Hz 是CPU的一次脈沖(可以理解為一次改變狀態(tài),也叫時(shí)鐘周期),稱之為為赫茲,那么1GHz等于多少赫茲呢
- 1GHz(兆赫)= 1000MHz(兆赫)
- 1MHz(兆赫)= 1百萬赫茲
所以 1GHz = 10億Hz,表示CPU可以一秒脈沖10億次(有10億個(gè)時(shí)鐘周期),這里不要簡單理解一個(gè)時(shí)鐘周期就是一次CPU運(yùn)算。
例如1 + 2 = 3,CPU要執(zhí)行四次才能完整這個(gè)操作,步驟一:把1放入寄存機(jī),步驟二:把2放入寄存器,步驟三:做加法,步驟四:保存3。
而且計(jì)算機(jī)的CPU也不會只運(yùn)行我們自己寫的程序上,同時(shí)CPU也要執(zhí)行計(jì)算機(jī)的各種進(jìn)程任務(wù)等等,我們的程序僅僅是其中的一個(gè)進(jìn)程而已。
所以我們的程序在計(jì)算機(jī)上究竟1s真正能執(zhí)行多少次操作呢?
做個(gè)測試實(shí)驗(yàn)
在寫測試程序測1s內(nèi)處理多大數(shù)量級數(shù)據(jù)的時(shí)候,有三點(diǎn)需要注意:
- CPU執(zhí)行每條指令所需的時(shí)間實(shí)際上并不相同,例如CPU執(zhí)行加法和乘法操作的耗時(shí)實(shí)際上都是不一樣的。
- 現(xiàn)在大多計(jì)算機(jī)系統(tǒng)的內(nèi)存管理都有緩存技術(shù),所以頻繁訪問相同地址的數(shù)據(jù)和訪問不相鄰元素所需的時(shí)間也是不同的。
- 計(jì)算機(jī)同時(shí)運(yùn)行多個(gè)程序,每個(gè)程序里還有不同的進(jìn)程線程在搶占資源。
盡管有很多因素影響,但是還是可以對自己程序的運(yùn)行時(shí)間有一個(gè)大體的評估的。
引用算法4里面的一段話:
- 火箭科學(xué)家需要大致知道一枚試射火箭的著陸點(diǎn)是在大海里還是在城市中;
- 醫(yī)學(xué)研究者需要知道一次藥物測試是會殺死還是會治愈實(shí)驗(yàn)對象;
所以任何開發(fā)計(jì)算機(jī)程序員的軟件工程師都應(yīng)該能夠估計(jì)這個(gè)程序的運(yùn)行時(shí)間是一秒鐘還是一年。
這個(gè)是最基本的,所以以上誤差就不算事了。
以下以C++代碼為例:
測試硬件:2015年MacPro,CPU配置:2.7 GHz Dual-Core Intel Core i5
實(shí)現(xiàn)三個(gè)函數(shù),時(shí)間復(fù)雜度分別是 O(n) , O(n^2), O(nlogn),使用加法運(yùn)算來統(tǒng)一測試。
- // O(n)
- void function1(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- k++;
- }
- }
- // O(n^2)
- void function2(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- for (long j = 0; j < n; j++) {
- k++;
- }
- }
- }
- // O(nlogn)
- void function3(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- for (long long j = 1; j < n; j = j*2) { // 注意這里j=1
- k++;
- }
- }
- }
來看一下這三個(gè)函數(shù)隨著n的規(guī)模變化,耗時(shí)會產(chǎn)生多大的變化,先測function1 ,就把 function2 和 function3 注釋掉
- int main() {
- long long n; // 數(shù)據(jù)規(guī)模
- while (1) {
- cout << "輸入n:";
- cin >> n;
- milliseconds start_time = duration_cast<milliseconds >(
- system_clock::now().time_since_epoch()
- );
- function1(n);
- // function2(n);
- // function3(n);
- milliseconds end_time = duration_cast<milliseconds >(
- system_clock::now().time_since_epoch()
- );
- cout << "耗時(shí):" << milliseconds(end_time).count() - milliseconds(start_time).count()
- <<" ms"<< endl;
- }
- }
來看一下運(yùn)行的效果,如下圖:
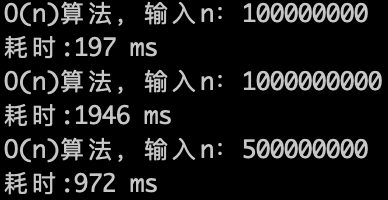
O(n)的算法,1s內(nèi)大概計(jì)算機(jī)可以運(yùn)行 5 * (10^8)次計(jì)算,可以推測一下O(n^2) 的算法應(yīng)該1s可以處理的數(shù)量級的規(guī)模是 5 * (10^8)開根號,實(shí)驗(yàn)數(shù)據(jù)如下。
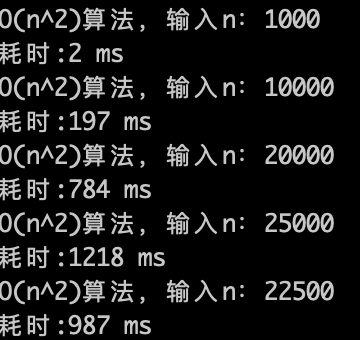
O(n^2)的算法,1s內(nèi)大概計(jì)算機(jī)可以運(yùn)行 22500次計(jì)算,驗(yàn)證了剛剛的推測。
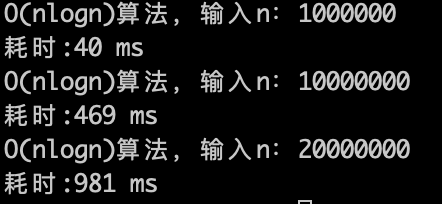
在推測一下O(nlogn)的話, 1s可以處理的數(shù)據(jù)規(guī)模是什么呢?
理論上應(yīng)該是比 O(n)少一個(gè)數(shù)量級,因?yàn)閘ogn的復(fù)雜度 其實(shí)是很快,看一下實(shí)驗(yàn)數(shù)據(jù)。
O(nlogn)的算法,1s內(nèi)大概計(jì)算機(jī)可以運(yùn)行 2 * (10^7)次計(jì)算,符合預(yù)期。
這是在我個(gè)人PC上測出來的數(shù)據(jù),不能說是十分精確,但數(shù)量級是差不多的,大家也可以在自己的計(jì)算機(jī)上測一下。
整體測試數(shù)據(jù)整理如下:
至于O(logn) 和O(n^3) 等等這些時(shí)間復(fù)雜度在1s內(nèi)可以處理的多大的數(shù)據(jù)規(guī)模,大家可以自己寫一寫代碼去測一下了。
完整測試代碼
- #include <iostream>
- #include <chrono>
- #include <thread>
- using namespace std;
- using namespace chrono;
- // O(n)
- void function1(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- k++;
- }
- }
- // O(n^2)
- void function2(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- for (long j = 0; j < n; j++) {
- k++;
- }
- }
- }
- // O(nlogn)
- void function3(long long n) {
- long long k = 0;
- for (long long i = 0; i < n; i++) {
- for (long long j = 1; j < n; j = j*2) { // 注意這里j=1
- k++;
- }
- }
- }
- int main() {
- long long n; // 數(shù)據(jù)規(guī)模
- while (1) {
- cout << "輸入n:";
- cin >> n;
- milliseconds start_time = duration_cast<milliseconds >(
- system_clock::now().time_since_epoch()
- );
- function1(n);
- // function2(n);
- // function3(n);
- milliseconds end_time = duration_cast<milliseconds >(
- system_clock::now().time_since_epoch()
- );
- cout << "耗時(shí):" << milliseconds(end_time).count() - milliseconds(start_time).count()
- <<" ms"<< endl;
- }
- }
總結(jié)
本文詳細(xì)分析了在leetcode上做題程序?yàn)槭裁磿谐瑫r(shí),以及從硬件配置上大體知道CPU的執(zhí)行速度,然后親自做一個(gè)實(shí)驗(yàn)來看看O(n)的算法,跑一秒鐘,這個(gè)n究竟是做大,最后給出不同時(shí)間復(fù)雜度,一秒內(nèi)可以運(yùn)算出來的n的大小。
建議錄友們也都自己做一做實(shí)驗(yàn),測一測,看看是不是和我的測出來的結(jié)果差不多。
這樣,大家應(yīng)該對程序超時(shí)時(shí)候的數(shù)據(jù)規(guī)模有一個(gè)整體的認(rèn)識了。