Dfs、Bfs的終于弄明白了
本文轉載自微信公眾號「bigsai」,作者大賽。轉載本文請聯系bigsai公眾號。
前言
你問一個人聽過哪些算法,那么深度優先搜索(dfs)和寬度優先搜索(bfs)那肯定在其中,很多小老弟學會dfs和bfs就覺得好像懂算法了,無所不能,確實如此,學會dfs和bfs暴力搜索枚舉確實利用計算機超強計算大部分都能求的一份解,學會dfs和bfs去暴力杯混分是一個非常不錯的選擇!
五大經典算法的回溯算法其實也是dfs的一種應用,是不是回憶起被折磨的八皇后問題。基礎的dfs和bfs學習來思想很容易,寫出來模板代碼也不難,但很多時候需要在此基礎上靈活變通就有不小難度了。
不過dfs 和bfs初步學習搞懂原理比較簡單,但是想要精通 dfs和bfs還是很難的,因為很多問題是在此基礎上進行變形優化的,比如dfs你可能考慮各種剪枝問題,bfs可能會涉及很多貪心的策略,有的還要考慮到記憶化的問題、雙向bfs、bfs+dfs等等才能更好解決的問題,不過本文講的相對基礎,不同的延伸需要自己刷題去學習才行。
鄰接矩陣和鄰接表
dfs和bfs一般用于處理圖論的問題,那么在看問題之前首先要關注圖的存儲問題,正常一般用鄰接矩陣或者鄰接表存儲圖(對于十字鏈表、壓縮矩陣之類空間優化這里不進行討論)。
鄰接矩陣:
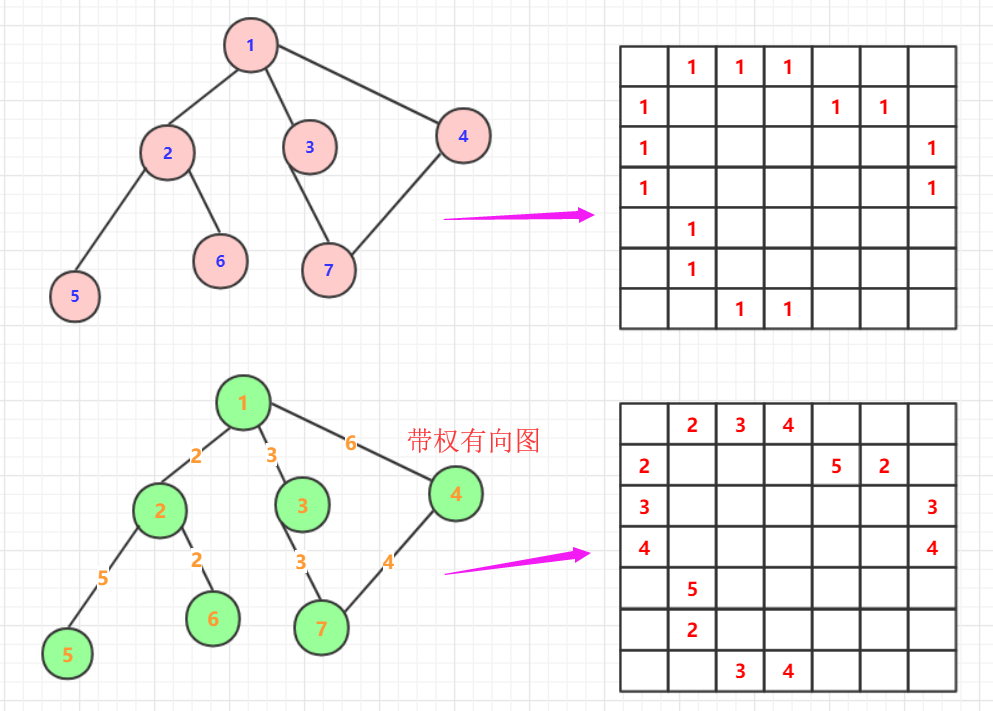
鄰接矩陣就是用數組(二維)表示圖,通常這種圖我們會對各個節點順序的編號,在矩陣內數值表示圖的聯通情況或者路徑長度。
如果是無權圖:那么一般用boolean數組的01表示聯通性,如果是有權圖那么數組的值就用來表示兩者路徑長度,如果為0那么就表示不通。另外如果圖是無向圖那么這個矩陣是對稱的,如果是有向圖那么大概率不是對稱的。
具體可以看下面例子,這種操作方式條理更清晰并且操作方便,當然,這種情況很容易造成空間浪費,所以有人進行空間優化,或者是鄰接表的方式存儲圖。
鄰接表:
觀察上面的鄰接矩陣,如果節點很多但是聯通路徑很少,那么就浪費了太多的存儲空間,這種情況就更適合鄰接表。
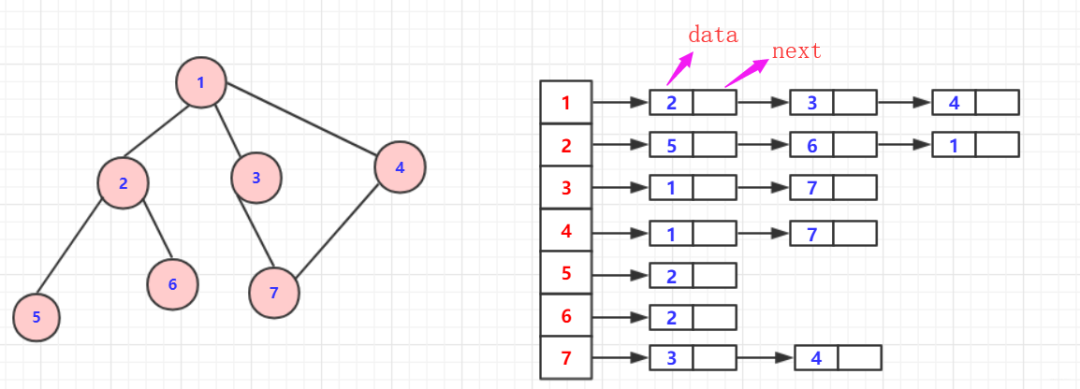
鄰接表一般是數組套鏈表,比起鄰接矩陣節省不少空間(直接存儲聯通信息或者路徑),在存儲的時候可以根據數據格式要求靈活運用容器(無權圖省事一些)。
但是正常的無向圖依然會重復浪費一半空間,就有十字鏈表,多重鏈接表等等出現優化(大佬們的優化是真的牛批),但在算法邏輯上稍復雜,不過一般圖論算法更注重的是算法的優化這里就不介紹十字鏈表等,一個鄰接表存儲的圖可以看下圖:
深度優先搜索(dfs)
概念:
深度優先搜索屬于圖算法的一種,英文縮寫為DFS即Depth First Search.其過程簡要來說是對每一個可能的分支路徑深入到不能再深入為止,而且每個節點只能訪問一次.
簡單的說,dfs就是在一個圖中按照一個規則進行搜索,一般基于遞歸實現,對于我們來說dfs就像一個黑魔法一樣,設計好算法它就自動搜索,所以我們要注意的是算法初始化、搜索規則、結束條件。二叉樹的前序遍歷就是一個最簡單的dfs遍歷。
我們通常使用鄰接表或者鄰接矩陣儲存圖的信息,這里例子使用鄰接矩陣完成!
對于dfs的流程來說,大致可以認為是這樣:
(1)某個節點開始先按照一個方向一直遍歷到盡頭,同時標記已經走過的點。
(2)遍歷到盡頭后回退到上一個點,同時清除當前點的標記。往下一個方向遍歷一次,然后繼續重復步驟(1).
(3)一直到所有流程都走完,即回退到起點。
在遍歷的過程中記得需要標記 因為不進行標記會出現死循環,標記就代表這個點被用過不能用了,而撤回標記就說明這個點又能重新使用了。
舉個例子,例如一個全排列s a i 當s被枚舉到就要標記這個s不能被使用(不可能ssss一直下去吧),并且遍歷到s a時候a也不能使用,到s a i 時候到盡頭回退 s a 依然要回退s 此時 a和i都被解但是上次指標方向為a(for 循環到的位置),那么下一次就要往下個方向i 組成s i,然后在s i a,同理回退到s i,到s,下面兩個方向都被枚舉過所以還要回退到,解放了s a i但是第一個方向s已經走過,開始從a 剩下的步驟依次類推就得到了。
不過全排列這是一維空間的dfs運用,在標記時候可以選擇boolean數組對應位置true標記用過,false表示沒用過。除此之外也可使用動態數組List使用過先刪除對應位置元素向下遞歸進行搜索,然后結束后再對應位置插入也行(不是很推薦,效率比較低)。
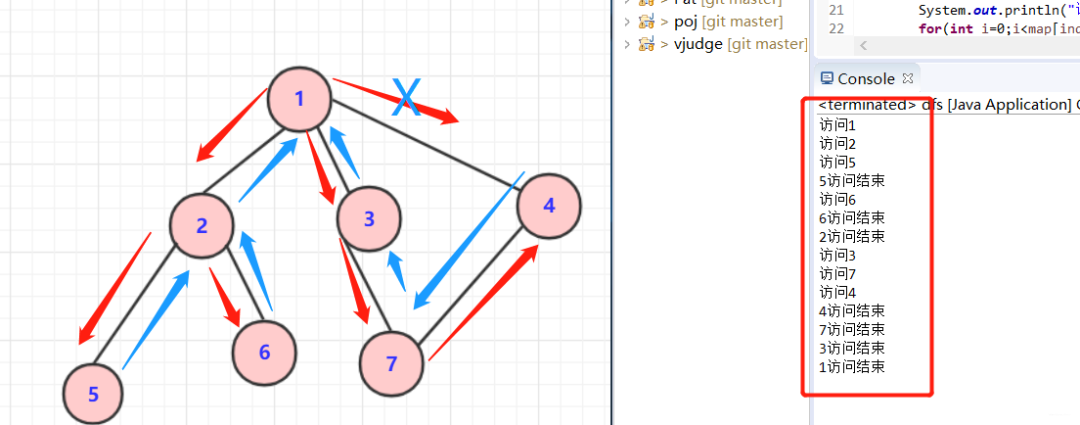
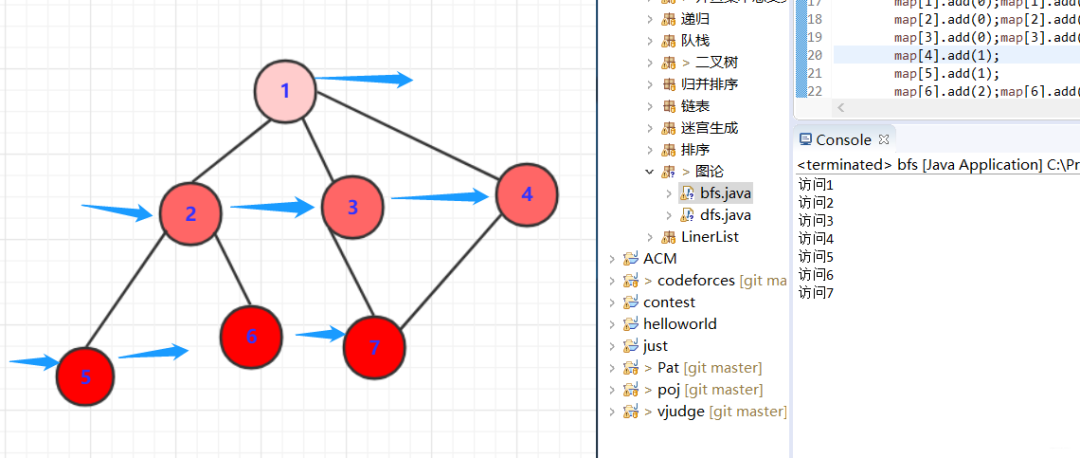
對于上面圖片中圖的dfs,得到其中一個dfs搜索的序列(可能有多個)可以用代碼來表示一下:
- public class dfs {
- static boolean isVisit[];
- public static void main(String[] args) {
- int map[][]=new int[7][7];
- isVisit=new boolean[7];
- map[0][1]=map[1][0]=1;
- map[0][2]=map[2][0]=1;
- map[0][3]=map[3][0]=1;
- map[1][4]=map[4][1]=1;
- map[1][5]=map[5][1]=1;
- map[2][6]=map[6][2]=1;
- map[3][6]=map[6][3]=1;
- isVisit[0]=true;
- dfs(0,map);//從0開始遍歷
- }
- private static void dfs(int index,int map[][]) {
- // TODO Auto-generated method stub
- System.out.println("訪問"+(index+1)+" ");
- for(int i=0;i<map[index].length;i++)//查找聯通節點
- {
- if(map[index][i]>0&&isVisit[i]==false)
- {
- isVisit[i]=true;
- dfs(i,map);
- }
- }
- System.out.println((index+1)+"訪問結束 ");
- }
- }
大致順序訪問為
廣度優先搜素(bfs)
概念:
BFS,其英文全稱是Breadth First Search。BFS并不使用經驗法則算法。從算法的觀點,所有因為展開節點而得到的子節點都會被加進一個先進先出的隊列中。一般的實驗里,其鄰居節點尚未被檢驗過的節點會被放置在一個被稱為 open 的容器中(例如隊列或是鏈表),而被檢驗過的節點則被放置在被稱為 closed 的容器中。(open-closed表)
簡單來說,bfs就是從某個節點開始按層遍歷,估計大部分人第一次接觸bfs的時候是在學習數據結構的二叉樹的層序遍歷!借助一個隊列一層一層遍歷。第二次估計就是在學習圖論的時候,給你一個圖,讓你寫出一個bfs遍歷的順序,此后再無bfs…
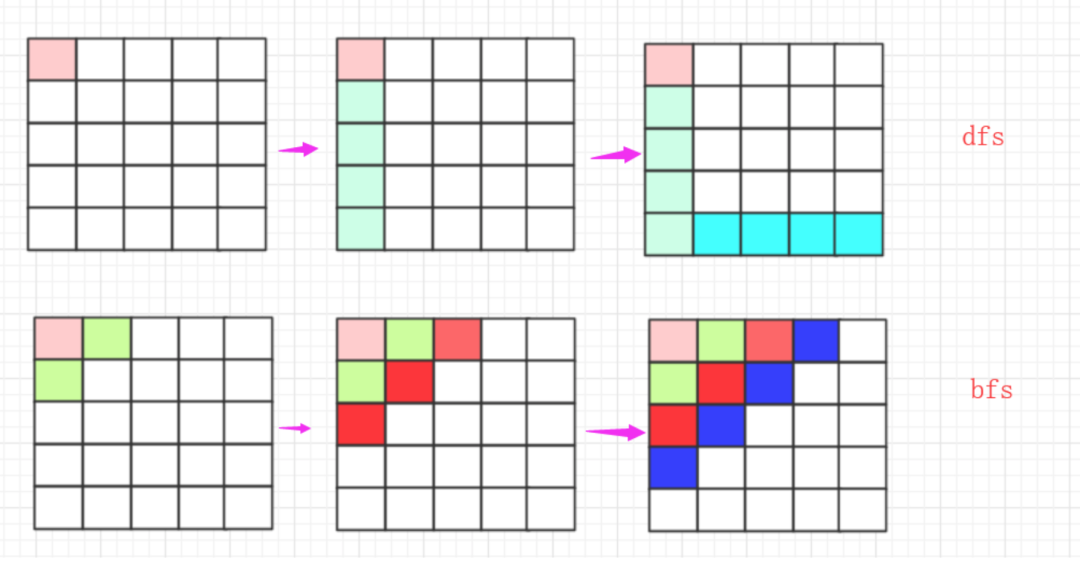
如果從路徑上走來看,dfs就是一條跑的很快的瘋狗,到處亂咬,沒路了就跑回來去其他地方繼續,而bfs就像是一團毒氣,慢慢延伸!
在實現上樸素的bfs就是控制一個隊列,后進先出進行層序遍歷,但很多時候可能有場景需求節點有權值可能就需要使用優先隊列。
就拿上述的圖來說,我們使用鄰接表來實現一個bfs遍歷。
- import java.util.ArrayDeque;
- import java.util.ArrayList;
- import java.util.List;
- import java.util.Queue;
- public class bfs {
- public static void main(String[] args) {
- List<Integer> map[]=new ArrayList[7];
- boolean isVisit[]=new boolean[7];
- for(int i=0;i<map.length;i++)//初始化
- {
- map[i]=new ArrayList<Integer>();
- }
- map[0].add(1);map[0].add(2);map[0].add(3);
- map[1].add(0);map[1].add(4);map[1].add(5);
- map[2].add(0);map[2].add(6);
- map[3].add(0);map[3].add(6);
- map[4].add(1);
- map[5].add(1);
- map[6].add(2);map[6].add(3);
- Queue<Integer>q1=new ArrayDeque<Integer>();
- q1.add(0);isVisit[0]=true;
- while (!q1.isEmpty()) {
- int va=q1.poll();
- System.out.println("訪問"+(va+1));
- for(int i=0;i<map[va].size();i++)
- {
- int index=map[va].get(i);
- if(!isVisit[index])
- {
- q1.add(index);
- isVisit[index]=true;
- }
- }
- }
- }
- }
搜索之延伸
本文主要任務是幫助初學者認清dfs和bfs,比較偏基礎,但是事實中dfs和bfs比較偏向實戰。
對于dfs和bfs,有些區別也有些共性,例如在迷宮很多問題dfs能解決bfs也能解決。
對于dfs一般解決的經典問題有:
- 二叉樹的搜索遍歷(非層序)
- 經典全排列、組合、子集問題
- 回溯算法之八皇后問題
- 迷宮搜索問題(能否找到)
- 其他圖搜索
而bfs一般解決的問題有:
- 二叉樹層序搜索遍歷(各種變形例如分層輸出、之字形等等空間優化)
- 無權圖的最短路徑
- 其他迷宮搜索問題(節點帶某些權值的)
- 其他問題
當然這里面羅列不全,dfs關注更多的可能是剪枝問題或者記憶化,剪枝就是剪掉沒必要的搜索,記憶化就是防止太多重復操作。而bfs關注更多的可能是貪心策略選擇(大部分搜索可能有一些附加的條件)可能需要使用優先隊列來解決。
然而,當數據達到一定程度,我們使用簡單的方法肯定會爆炸的。就可能需要一些特殊的巧妙方法處理,比如想不到的剪枝優化、優先隊列、A*、dfs套bfs,又或者利用一些非常厲害的數學方法比如康托展開(逆展開)等等。而今天在這里,我們談談雙向bfs,體驗一下算法的奧妙!
什么樣的情況可以使用雙向bfs來優化呢?其實雙向bfs的主要思想是問題的拆分吧,比如在一個迷宮中可以往下往右行走,問你有多少種方式從左上到右下。
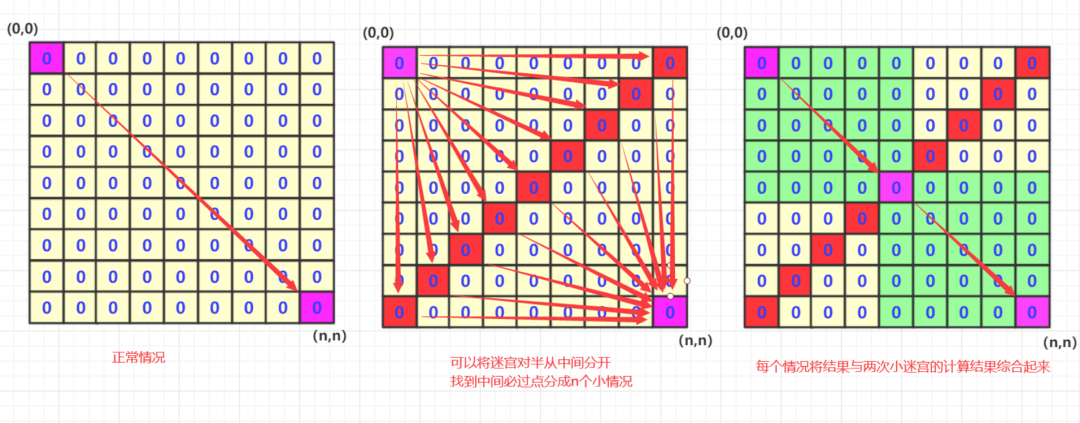
正常情況下,我們就是搜索遍歷,如果迷宮邊長為n,那么這個復雜度大概是2^n級別.
但是實際上我們可以將迷宮拆分一下,比如根據對角線(比較多),將迷宮一分為二。其實你的結果肯定必然經過對角線的這些點對吧!我們只要分別計算出各個對角線各個點的次數然后相加就可以了!
怎么算? 就是從(0,0)到中間這個點mid的總次數為n1,然后這個mid到(n,n)點的總次數為n2,然后根據排列組合總次數就是n1*n2(n1和n2正常差不多大)這樣就可以通過乘法減少加法的運算次數啦!
簡單的說,從數據次數來看如果直接搜索全圖經過下圖的那個點的次數為n1*n2次,如果分成兩個部分相乘那就是n1+n2次。兩者差距如果n1,n2=1000左右,那么這么一次差距是平方(根號)級別的。從搜索圖形來看其實這么一次搜索是本來一個n*n大小的搜索轉變成n次(每次大概是(n/2)*(n/2)大小的迷宮搜索兩次)。也就是如果18*18的迷宮如果使用直接搜索,那么大概2^18次方量級,而如果采用雙向bfs,那么就是2^9這個量級。
例題實戰一下,就拿一道經典雙向bfs問題給大家展示一下吧!
題目鏈接:http://oj.hzjingma.com/contest/problem?id=20&pid=8#problem-anchor
分析:對于題目的要求還是很容易理解的,就是找到所有的路徑種類,再判斷其中是對稱路徑的有幾個輸出即可!
對于一個普通思考是這樣的,首先是進行dfs,然后動態維護一個字符串,每次跑到最后判斷這個路徑字符串是否滿足對稱要求,如果滿足那么就添加到容器中進行判斷。可惜很遺憾這樣是超時的,僅能通過40%的樣例。
接著用普通bfs進行嘗試,維護一個node節點,每次走的時候路徑儲存起來其實這個效率跟dfs差不多依然超時。只能通過40%數據。
接下來就開始雙向bfs進行分析!
(1) 既然只能右下,那么對角線的那個位置的肯定是中間的那個字符串的!它的存在不影響是否對稱的(n*n的迷宮路徑長度為n-1 + n為奇數).
(2) 我們判斷路徑是否對稱,只需要判斷從(1,1)到對角節點k(設為k節點)的路徑有沒有和從(n,n)到k相同的。如果有路徑相同的那么就說明這一對構成對稱路徑
(3) 在具體實現上,我們對每個對角線節點可以進行兩次bfs(一次左上到(1,1),一次右下到(n,n)).并且將路徑放到兩個hashset(set1,set2)中,跑完之后用遍歷其中一個hashset中的路徑,看看另一個set是否存在該路徑,如果存在就說明這個是對稱路徑放到 總的hashset(set) 中。對角線每個位置都這樣判斷完最后只需要輸出總的hashset(set)的集合大小即可!
ac代碼如下:
- import java.util.ArrayDeque;
- import java.util.HashSet;
- import java.util.Queue;
- import java.util.Scanner;
- import java.util.Set;
- public class test2 {
- static class node{
- int x;
- int y;
- String path="";
- public node() {}
- public node(int x,int y,String team)
- {
- this.x=x;
- this.y=y;
- this.path=team;
- }
- }
- public static void main(String[] args) {
- Scanner sc=new Scanner(System.in);
- Set<String>set=new HashSet<String>();//儲存最終結果
- int n=Integer.parseInt(sc.nextLine());
- char map[][]=new char[n][n];
- for(int i=0;i<n;i++)
- {
- String string=sc.nextLine();
- map[i]=string.toCharArray();
- }
- Queue<node>q1=new ArrayDeque<node>();//左上的隊列
- Queue<node>q2=new ArrayDeque<node>();//右下的隊列
- for(int i=0;i<n;i++)
- {
- q1.clear();q2.clear();
- Set<String>set1=new HashSet<String>();//儲存zuoshang
- Set<String>set2=new HashSet<String>();//儲右下
- q1.add(new node(i,n-1-i,""+map[i][n-1-i]));
- q2.add(new node(i,n-1-i,""+map[i][n-1-i]));
- while(!q1.isEmpty()&&!q2.isEmpty())
- {
- node team=q1.poll();
- node team2=q2.poll();
- if(team.x==n-1&&team.y==n-1)//到終點,將路徑儲存
- {
- //System.out.println(team2.path);
- set1.add(team.path);
- set2.add(team2.path);
- }
- else {
- if(team.x<n-1)//可以向下
- {
- q1.add(new node(team.x+1, team.y, team.path+map[team.x+1][team.y]));
- }
- if(team.y<n-1)//可以向右
- {
- q1.add(new node(team.x, team.y+1, team.path+map[team.x][team.y+1]));
- }
- if(team2.x>0)//上
- {
- q2.add(new node(team2.x-1, team2.y, team2.path+map[team2.x-1][team2.y]));
- }
- if(team2.y>0)//左
- {
- q2.add(new node(team2.x, team2.y-1, team2.path+map[team2.x][team2.y-1]));
- }
- }
- }
- for(String va:set1)
- {
- if(set2.contains(va))
- {
- set.add(va);
- }
- }
- }
- System.out.println(set.size());
- }
- }
總結
dfs和bfs是圖論中非常經典的搜索算法,兩種算法的重要程度都非常高,這里面主要對其簡單介紹,對于普通開發者,能夠用dfs和bfs能夠解決二叉樹問題、迷宮搜索問題等基礎簡單的就夠了(面試官不會那么騷難為你)。
如果理解比較困難,多看教程、多刷題,多刷題之后每做一題算法跑的大概流程是有個數的。