讓我們一起復習回溯算法理論基礎,你還記得嗎?
回溯算法其實非常晦澀難懂,建議大家配合我的B站視頻,來學習回溯算法,相信看完之后,會解開你對回溯算法的種種疑惑。
什么是回溯法
回溯法也可以叫做回溯搜索法,它是一種搜索的方式。
在二叉樹系列中,我們已經不止一次,提到了回溯,例如二叉樹:以為使用了遞歸,其實還隱藏著回溯。
回溯是遞歸的副產品,只要有遞歸就會有回溯。
所以以下講解中,回溯函數也就是遞歸函數,指的都是一個函數。
回溯法的效率
回溯法的性能如何呢,這里要和大家說清楚了,雖然回溯法很難,很不好理解,但是回溯法并不是什么高效的算法。
因為回溯的本質是窮舉,窮舉所有可能,然后選出我們想要的答案,如果想讓回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是窮舉的本質。
那么既然回溯法并不高效為什么還要用它呢?
因為沒得選,一些問題能暴力搜出來就不錯了,撐死了再剪枝一下,還沒有更高效的解法。
此時大家應該好奇了,都什么問題,這么牛逼,只能暴力搜索。
回溯法解決的問題
回溯法,一般可以解決如下幾種問題:
- 組合問題:N個數里面按一定規則找出k個數的集合
- 切割問題:一個字符串按一定規則有幾種切割方式
- 子集問題:一個N個數的集合里有多少符合條件的子集
- 排列問題:N個數按一定規則全排列,有幾種排列方式
- 棋盤問題:N皇后,解數獨等等
相信大家看著這些之后會發現,每個問題,都不簡單!
另外,會有一些同學可能分不清什么是組合,什么是排列?
組合是不強調元素順序的,排列是強調元素順序。
例如:{1, 2} 和 {2, 1} 在組合上,就是一個集合,因為不強調順序,而要是排列的話,{1, 2} 和 {2, 1} 就是兩個集合了。
記住組合無序,排列有序,就可以了。
如何理解回溯法
回溯法解決的問題都可以抽象為樹形結構,是的,我指的是所有回溯法的問題都可以抽象為樹形結構!
因為回溯法解決的都是在集合中遞歸查找子集,集合的大小就構成了樹的寬度,遞歸的深度,都構成的樹的深度。
遞歸就要有終止條件,所以必然是一顆高度有限的樹(N叉樹)。
這塊可能初學者還不太理解,后面的回溯算法解決的所有題目中,我都會強調這一點并畫圖舉相應的例子,現在有一個印象就行。
回溯法模板
這里給出Carl總結的回溯算法模板。
在講二叉樹的遞歸中我們說了遞歸三部曲,這里我再給大家列出回溯三部曲。
- 回溯函數模板返回值以及參數
在回溯算法中,我的習慣是函數起名字為backtracking,這個起名大家隨意。
回溯算法中函數返回值一般為void。
再來看一下參數,因為回溯算法需要的參數可不像二叉樹遞歸的時候那么容易一次性確定下來,所以一般是先寫邏輯,然后需要什么參數,就填什么參數。
但后面的回溯題目的講解中,為了方便大家理解,我在一開始就幫大家把參數確定下來。
回溯函數偽代碼如下:
- void backtracking(參數)
- 回溯函數終止條件
既然是樹形結構,那么我們在講解二叉樹的遞歸的時候,就知道遍歷樹形結構一定要有終止條件。
所以回溯也有要終止條件。
什么時候達到了終止條件,樹中就可以看出,一般來說搜到葉子節點了,也就找到了滿足條件的一條答案,把這個答案存放起來,并結束本層遞歸。
所以回溯函數終止條件偽代碼如下:
- if (終止條件) {
- 存放結果;
- return;
- }
- 回溯搜索的遍歷過程
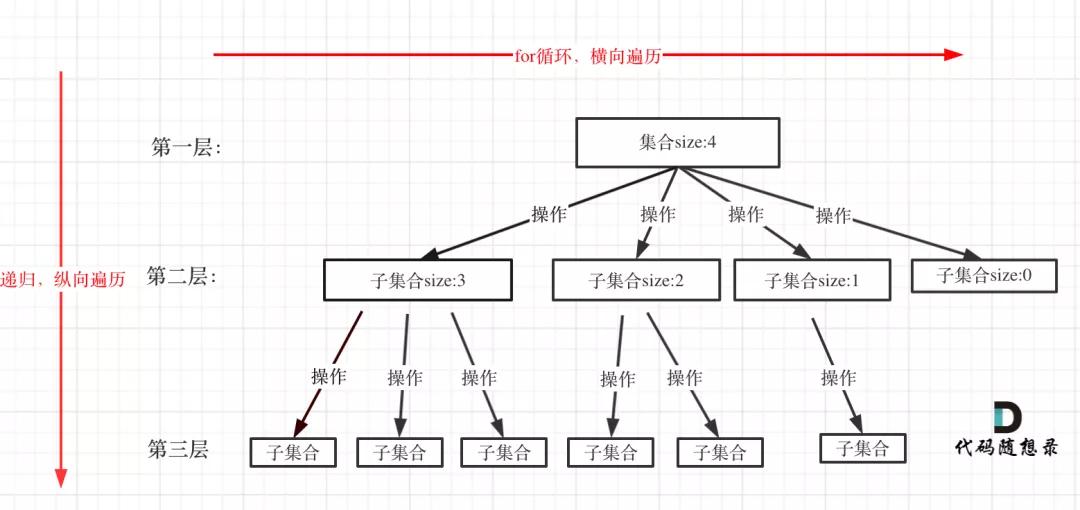
在上面我們提到了,回溯法一般是在集合中遞歸搜索,集合的大小構成了樹的寬度,遞歸的深度構成的樹的深度。
如圖:
回溯算法理論基礎
注意圖中,我特意舉例集合大小和孩子的數量是相等的!
回溯函數遍歷過程偽代碼如下:
- for (選擇:本層集合中元素(樹中節點孩子的數量就是集合的大小)) {
- 處理節點;
- backtracking(路徑,選擇列表); // 遞歸
- 回溯,撤銷處理結果
- }
for循環就是遍歷集合區間,可以理解一個節點有多少個孩子,這個for循環就執行多少次。
backtracking這里自己調用自己,實現遞歸。
大家可以從圖中看出for循環可以理解是橫向遍歷,backtracking(遞歸)就是縱向遍歷,這樣就把這棵樹全遍歷完了,一般來說,搜索葉子節點就是找的其中一個結果了。
分析完過程,回溯算法模板框架如下:
- void backtracking(參數) {
- if (終止條件) {
- 存放結果;
- return;
- }
- for (選擇:本層集合中元素(樹中節點孩子的數量就是集合的大小)) {
- 處理節點;
- backtracking(路徑,選擇列表); // 遞歸
- 回溯,撤銷處理結果
- }
- }
這份模板很重要,后面做回溯法的題目都靠它了!
如果從來沒有學過回溯算法的錄友們,看到這里會有點懵,后面開始講解具體題目的時候就會好一些了,已經做過回溯法題目的錄友,看到這里應該會感同身受了。
總結
本篇我們講解了,什么是回溯算法,知道了回溯和遞歸是相輔相成的。
接著提到了回溯法的效率,回溯法其實就是暴力查找,并不是什么高效的算法。
然后列出了回溯法可以解決幾類問題,可以看出每一類問題都不簡單。
最后我們講到回溯法解決的問題都可以抽象為樹形結構(N叉樹),并給出了回溯法的模板。