面試官問我索引為什么這快?我好像解釋不清楚了
阿粉相信大家肯定都知道,在數據庫中加一定量的索引,會讓你的查詢語句,從原來的 3 秒縮短到零點幾秒的程度,但是很多人都不知道為什么要加索引,為什么加了索引之后,你的查詢語句就會起飛呢?今天阿粉來聊一下索引。
索引的類型(常見的)
- 主鍵索引(primary key):主鍵索引這個阿粉從剛開始接觸開發的時候,就被各種灌輸,表的主鍵就默認是索引,不允許出現空值。
- 普通索引(index/normal):MySQL中基本索引類型,沒有什么限制,允許在定義索引的列中插入重復值和空值。
- 全文索引(fulltext):只能在文本類型CHAR,VARCHAR,TEXT類型字段上創建全文索引。MyISAM和InnoDB中都可以使用全文索引。
- 唯一索引(unique):索引列中的值必須是唯一的,但是允許為空值。
索引的類型肯定不限制于這幾項,既然我們知道分類了,我們接下來再來看看不同索引的創建方式。
不同索引的創建方式
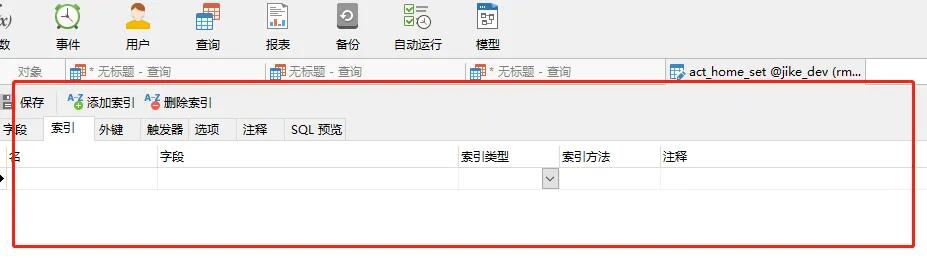
其實如果你真的不會去寫 SQL 去創建索引,最簡單的,Navicat 你總是會用的吧,圖形化的界面操作,你肯定也是了解的吧,那圖形化直接操作不就好了。
這樣子操作是不是簡單明了,選擇你想要創建索引的類型,然后指名你想要創建索引的字段,最后再給他加上個注釋,完美解決,但是我們還是要寫語句來看一下的。
1. 創建普通的索引
- ALTER TABLE table_name ADD INDEX index_name (column)
比如我們有一張表叫做 user 我們想給 user 表中的一個叫做 phone 字段增加一個索引,應該怎么去寫呢?
- ALTER TABLE user ADD INDEX phoneIndex (phone)
這時候我們就創建好了一個索引了,索引的刪除,相對來說也是非常的簡單。其實說是創建索引,實際上就是給我們原有表中的某個字段上增加一個索引,這個大家一定得清楚哈,千萬別和 Create 給搞混了。下面阿粉就直接簡單的給大家稱之為創建吧。
- ALTER TABLE testalter_tb1 DROP INDEX index_name
這樣刪除我們剛才建立的索引就是
- ALTER TABLE user DROP INDEX phoneIndex
這時候我們就能看到刪除成功了。
- > OK
- > 時間: 0.012s
2. 創建唯一索引(unique)并刪除
- ALTER TABLE user ADD unique phoneIndex (phone)
- ALTER TABLE user DROP INDEX phoneIndex;
千萬不要想當然的認為創建的時候我指定了索引的類型,然后刪除的時候也執行一個 ALTER TABLE user DROP unique phoneIndex; 阿粉親身實踐,確實是不成功的。
3. 創建主鍵索引(primary key)并刪除
- ALTER TABLE user ADD PRIMARY KEY (phone):
- ALTER TABLE user DROP PRIMARY KEY
一般我們在建表的時候,都把這個主鍵索引都建好了,所以使用的場景并不是很多見。
4. 創建全文索引(fulltext)并刪除
創建方式都差不多就是這樣
- ALTER TABLE user ADD FULLTEXT phoneIndex (phone)
- ALTER TABLE user DROP INDEX phoneIndex;
既然我們了解了創建的方式了,那是不是該回歸正題,說說為什么使用索引就會快,這就得涉及到索引的底層知識了,
索引的實現
在沒有索引的情況下,我們查找數據只能按照從頭到尾的順序逐行查找,每查找一行數據,意味著我們要到到磁盤相應的位置去讀取一條數據。
如果把查詢一條數據分為到磁盤中查詢和比對查詢條件兩步的話,到磁盤中查詢的時間會遠遠大于比對查詢條件的時間,這意味著在一次查詢中,磁盤io占用了大部分的時間。更進一步地說,一次查詢的效率取絕于磁盤io的次數,如果我們能夠在一次查詢中盡可能地降低磁盤io的次數,那么我們就能加快查詢的速度。
所以我們就要開始引入索引,然后分析索引底層是如何實現查找迅速的。
實際上索引的底層實際上就是樹,也就 B 樹和 B+ 樹,也可以稱之為變種的 B+ 樹。大家也都知道 Mysql中最常用的引擎像InnoDB和MyISAM,最終都選擇了B+樹作為索引。
那我們來說說這個B樹和B+樹。
B-樹,也稱為B樹,是一種平衡的多叉樹(可以對比一下平衡二叉查找樹),它比較適用于對外查找。
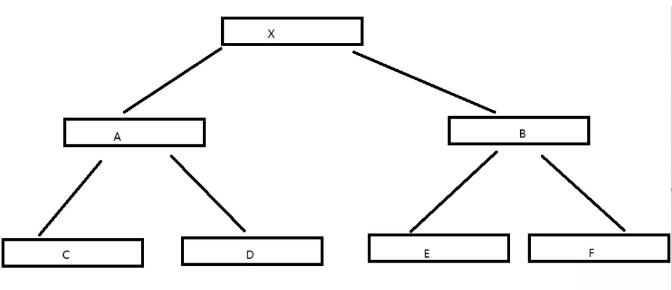
畫一個二階B樹:
二階B樹
那么我們為什么稱他為二階 B 樹呢?這個階數實際上就是說一個 節點 最多有幾個 子節點。
我們上面的圖,X元素,有2個子節點,A 元素,又有2個 子節點 C 和 D ,而 B 元素,又有 2 個子節點 E F ,也就是說一個節點最多有多少個子節點,我們就稱它為幾階的樹,通常這個值一般用 m 來表示。
注意我們所說的,也就是一個節點上 最多 的子節點數,如果有一個分支是有三個節點,而有一個是 兩個節點 ,那我們就稱它為 三階 B 樹。
一顆m階的 B 樹 要滿足什么條件呢?
- 每個節點至多可以擁有m棵子樹。
- 根節點,只有至少有2個節點(要么極端情況,就是一棵樹就一個根節點,單細胞生物,即是根,也是葉,也是樹)。
- 非根非葉的節點至少有的Ceil(m/2)個子樹(Ceil表示向上取整,圖中3階B樹,每個節點至少有2個子樹,也就是至少有2個叉)。
- 非葉節點中的信息包括[n,A0,K1,A1,K2,A2,…,Kn,An],,其中n表示該節點中保存的關鍵字個數,K為關鍵字且Ki
- 從根到葉子的每一條路徑都有相同的長度,也就是說,葉子節點在相同的層,并且這些節點不帶信息,實際上這些節點就表示找不到指定的值,也就是指向這些節點的指針為空。
B樹的查詢過程和二叉排序樹比較類似,從根節點依次比較每個節點,因為每個節點中的關鍵字和左右子樹都是有序的,所以只要比較節點中的關鍵字,或者沿著指針就能很快地找到指定的關鍵字,如果查找失敗,則會返回葉子節點,即空指針。
B樹搜索的簡單偽算法如下:
- BTree_Search(node, key) {
- if(node == null) return null;
- foreach(node.key)
- {
- if(node.key[i] == key) return node.data[i];
- if(node.key[i] > key) return BTree_Search(point[i]->node);
- }
- return BTree_Search(point[i+1]->node);
- }
- data = BTree_Search(root, my_key);
這就是個偽算法,寫的不好,大家見諒,那么什么是 B+ 樹呢?
B+ 樹是一種樹數據結構,是一個n叉樹,每個節點通常有多個孩子,一顆B+樹包含根節點、內部節點和葉子節點。根節點可能是一個葉子節點,也可能是一個包含兩個或兩個以上孩子節點的節點。
B+ 樹通常用于數據庫和操作系統的文件系統中。
NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和BFS等文件系統都在使用B+樹作為元數據索引。
B+ 樹的特點是能夠保持數據穩定有序,其插入與修改擁有較穩定的對數時間復雜度。
B+ 樹元素自底向上插入。
那 B+ 樹又有哪些比較顯著的特點呢?
- 每個父節點的元素都出現在了子節點中,分別是子節點最大或者最小的元素。
- 在上面的這一棵樹中,根節點元素8是子節點258的最大的元素,根元素15也是。這時候要注意了,根節點最大的元素等同于整個B+樹的最大的元素,以后無論是怎么插入或者是刪除,始終都要保持最大的元素在根節點中。
- 葉子節點,因為父節點的元素都出現在了子節點當中,因此所有的葉子節點包含了全量的元素信息。
B+樹與B樹差異
- 有k個子節點的節點必然有k個元素
- 非葉子節點僅具有索引作用,跟記錄有關的信息均存放在葉子節點中
- 樹的所有葉子節點構成一個有序鏈表,可以按照元素排序的次序遍歷全部記錄
- B樹和B+樹的區別在于,B+樹的非葉子節點只包含導航信息,不包含實際的值,所有的葉子節點和相連的節點使用鏈表相連,便于區間查找和遍歷。
說到這里,就會有讀者開始想,說了半天,沒有說到重點,為什么加了索引就快呢?
剛才阿粉也說了,數據庫讀取數據,是從磁盤上通過 IO 來進行數據的操作,一次磁盤IO操作可以取出物理存儲中相鄰的一大片數據,如果查詢的索引數據(就是B+樹中從根節點一直到葉子節點整個過程中查詢的節點數)都集中在該區域,那么只需要一次磁盤IO,否則就需要多次磁盤IO。
這么說是不是就相對的簡單明了了。
再舉出一個簡單的例子:
比如我們想要查詢 user 表中 name 為 xiaohong 的數據,在我們寫 SQL 的時候
- select * from user where name = 'xiaohong'
這時候沒有索引的情況下,數據庫直接就把整個表全部掃描一遍,然后去找 name = ‘xiaohong’ 的數據
而我們給他加上索引之后,會通過索引查找去查詢名為 ‘xiaohong‘ 的數據,因為該索引已經按照字母順序排列,因此要查找名為 ‘xiaohong' 的記錄時會快很多。
大家明白了么?就像是一個詞典,我把 x 開頭的數據都給你羅列出來,然后你從 x 開頭的數據中去尋找,和你直接沒有任何處理,直接一頁一頁的翻詞典的速度,哪一個更快,相信大家也都明白了吧。