清華大學(第一作者為王建勇教授的在讀博士生王焯)聯合華東師范大學(張偉,2016 年博士畢業于清華大學)和山東大學(劉寧,2021 年博士畢業于清華大學)提出了一種基于規則表征學習的分類模型 RRL。RRL 同時具備類似決策樹模型的高可解釋性和類似隨機森林和 XGBoost 等集成學習器的分類性能。相關論文已入選 NeurIPS2021。

- 論文鏈接:https://arxiv.org/abs/2109.15103
- 代碼鏈接:https://github.com/12wang3/rrl
為了同時獲得良好的可解釋性和分類性能,論文提出了一種新的分類模型——規則表征學習器(RRL)。RRL 能夠通過自動學習可解釋的非模糊規則進行數據表征和分類。為了高效地訓練不可導的 RRL 模型,論文提出了一種新的訓練方法——梯度嫁接法。借助梯度嫁接法,離散的 RRL 可以直接使用梯度下降法進行優化。此外,論文還設計了一種改進版的邏輯激活函數,既提高了 RRL 的可擴展性,又使其能夠端到端地離散化連續特征。
在九個小規模和四個大規模數據集上的實驗表明,RRL 的分類性能顯著優于其他可解釋方法(如第二屆「AI 諾獎」得主 Cynthia Rudin 教授團隊提出的 SBRL),并能與不可解釋的復雜模型(如集成學習模型隨機森林和 XGBoost、分段線性神經網絡 PLNN)取得近似的分類性能。此外,RRL 能夠方便地在分類精度和模型復雜度之間進行權衡,進而滿足不同場景的需求。
研究背景與動機
盡管深度神經網絡已在很多機器學習任務中取得了令人矚目的成果,其不可解釋的特性仍使其飽受詬病。即使人們可以使用代理模型(Surrogate Models),隱層探查法(Hidden Layer Investigation),以及其他事后(Post-hoc)方法對深度網絡進行解釋,這些方法的忠實度、一致性和具體程度都存在或多或少的問題。
反觀基于規則的模型(Rule-based Model),例如決策樹,得益于其透明的內部結構和良好的模型表達能力,仍在醫療、金融和政治等對模型可解釋性要求較高的領域發揮著重要作用。然而,傳統的基于規則的模型由于其離散的參數和結構而難以優化,尤其在大規模數據集上,這嚴重限制了規則模型的應用范圍。而集成模型、軟規則和模糊規則等,雖然提升了分類預測能力,但犧牲了模型可解釋性。
為了在更多場景中利用規則模型的優勢,迫切需要解決以下問題:如何在保持可解釋性的同時提高基于規則的模型的可擴展性?
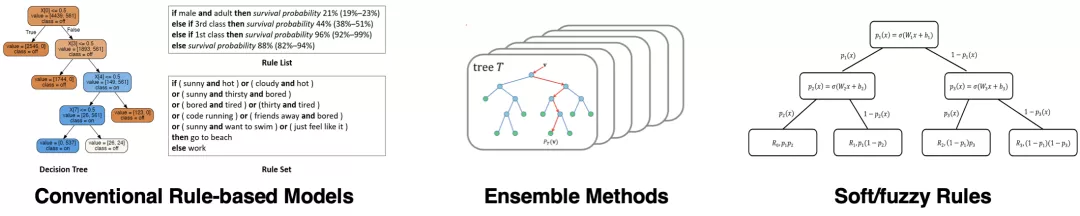
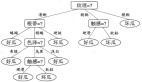
圖 1:傳統的基于規則的模型及其拓展模型
規則表征學習器
為了解決以上問題,論文提出了一種新的基于規則的模型,規則表征學習器(Rule-based Representation Learner, RRL),用于可解釋分類任務。為了獲得良好的模型透明度和表達能力,RRL 被設計為一個層級模型(如圖 2 所示),由一個二值化層,若干邏輯層,一個線性層,以及層與層之間的連邊構成:
二值化層(Binarization Layer)
- 用于對連續值特征進行劃分。
- 結合邏輯層可實現特征端到端離散化。
邏輯層(Logical Layer)
- 用于自動學習規則表征。
- 每個邏輯層由一個合取層和一個析取層構成。
- 兩層邏輯層即可表示合取范式和析取范式。
線性層(Linear Layer)
- 用于輸出分類結果。
- 可以更好地擬合數據的線性部分.
- 權重可用于衡量規則重要度。
跳連接(Skip Connection)
- 用于自動跳過不必要的層。
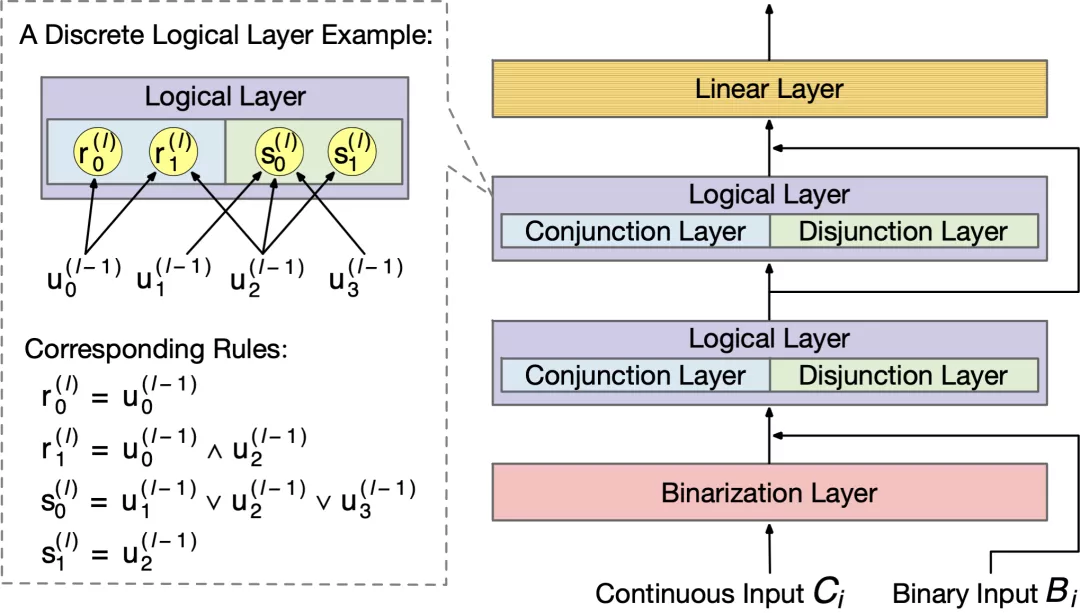
圖 2:規則表征學習器舉例。虛線框中展示了一個離散邏輯層及其對應的規則。
邏輯層
邏輯層(Logical Layer)使用邏輯規則自動學習數據表征。為了實現這一點,邏輯層被設計為同時具有離散版本和連續版本。二者共用參數,但離散版本用于訓練、測試和解釋,而連續版本僅用于訓練。
離散邏輯層
邏輯層中的每個節點都代表了一個邏輯運算,包括合取和析取,而層與層之間邊的連接則指明了運算有哪些變量參與。離散邏輯層節點對應的邏輯運算如下,其中
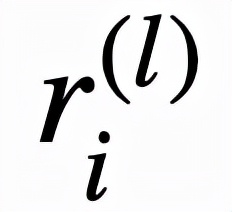
和
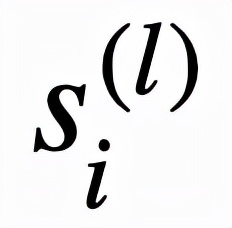
分別為合取層和析取層中的節點,
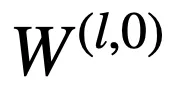
和
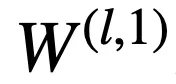
則是鄰接矩陣。圖 2 虛線框中展示了一個離散邏輯層的具體例子。
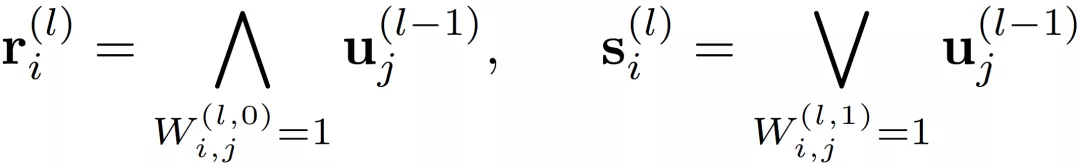
通過學習邊的連接,邏輯層便可以靈活地表示有著合取或析取范式形式的離散分類規則。然而問題在于,雖然離散的邏輯層可解釋性好,但自身不可導,難以訓練,這也是為什么還需要一個對應的連續版本的邏輯層。
連續邏輯層
連續邏輯層必須是可導的,并且當二值化連續邏輯層的參數時,可以直接得到它相對應的離散邏輯層。為此需要:
- 將 0/1 鄰接矩陣替換為 [0, 1] 之間的實數權重矩陣
- 用邏輯激活函數替換邏輯運算
傳統的邏輯激活函數(Payani and Fekri, 2019)如下,其中
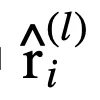
和
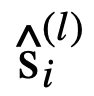
分別為連續合取層和連續析取層中的節點。
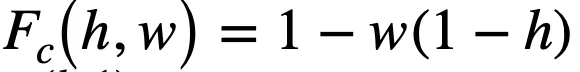
而
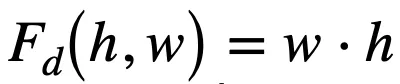
,二者通過
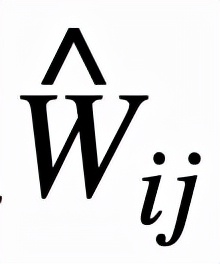
的大小來決定
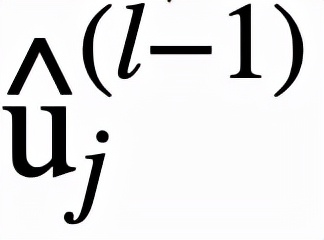
對最終結果的影響的大小。
如果
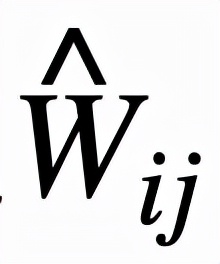
=0,則
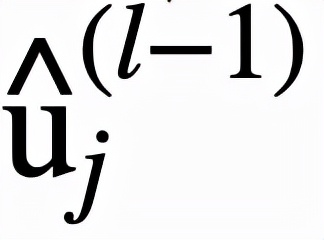
對最終結果沒有影響。
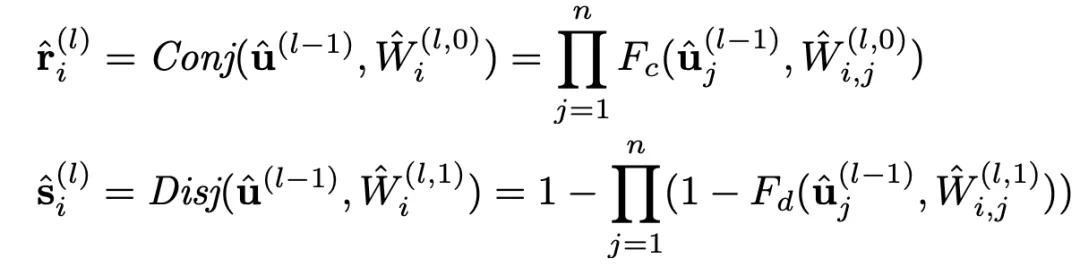
雖然這兩個邏輯激活函數能夠較好地用可導的實數運算模擬邏輯運算,但其存在嚴重的梯度消失問題,無法處理特征數較多的情況,可擴展性較差。分析邏輯激活函數
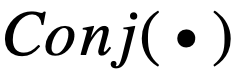
和
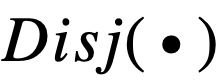
以及相應的導數可以發現,使用連乘來模擬邏輯運算是導致梯度消失的主要原因。
以
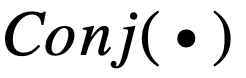
為例,其對應導數如下:
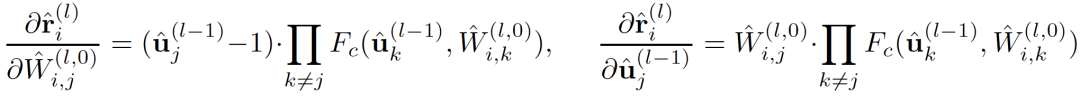
由于
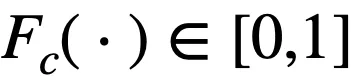
,則當相乘的
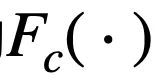
數量較多時(一般指特征數較多或節點數較多),導數結果都會趨向于 0,即出現了梯度消失的問題。
邏輯激活函數改進
傳統邏輯激活函數因為使用連乘模擬邏輯運算,因而在處理較多特征時會產生梯度消失的問題,嚴重損害了模型的可擴展性。一個直接的改進思路是使用對數函數將連乘轉化為連加。然而對數函數使得激活函數無法保持邏輯運算的特性。因而需要一個映射函數
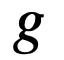
,該映射函數至少需要滿足以下三個條件:
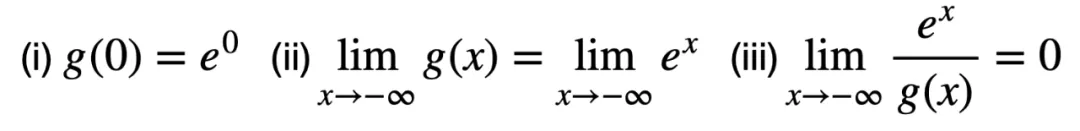
條件 (i) 和(ii)用于保持邏輯激活函數的范圍和趨勢,而條件 (iii) 要求
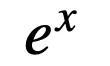
是
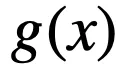
的高階無窮小,主要用于減緩當
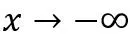
時其趨向于 0 的速度。
取
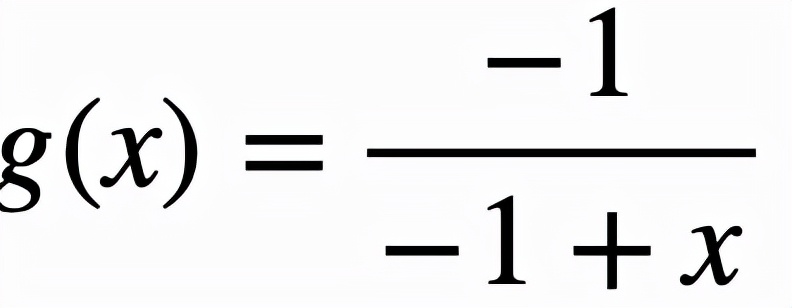
,這樣對邏輯激活函數的改進可以
總結為
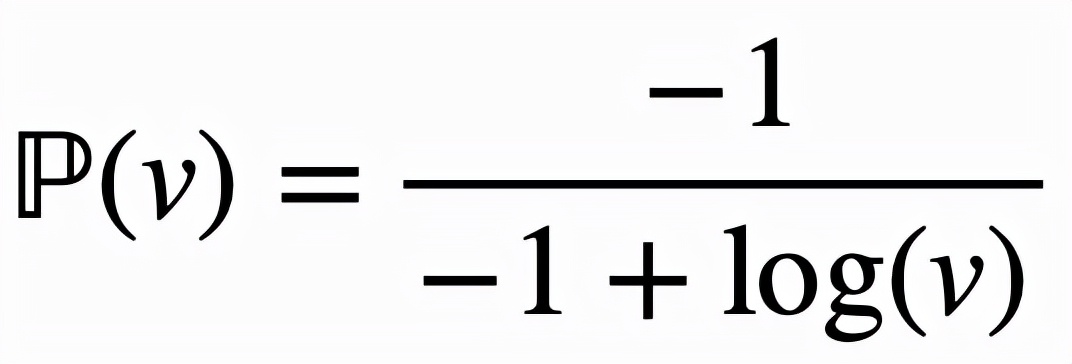
,而改進后的邏輯激活函數為:
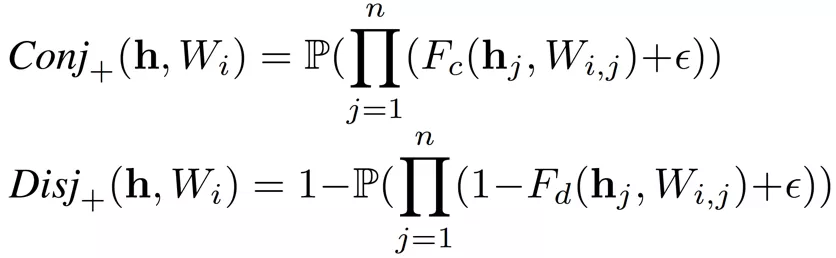
二值化層
二值化層主要用于將連續的特征值劃分為若干個單元。對于第 j 個連續值特征
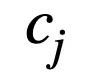
,有 k 個隨機下界
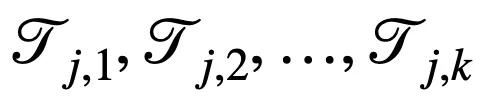
和 k 個隨機上界
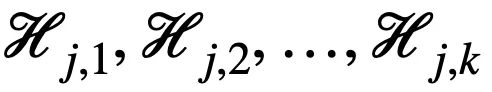
對其進行劃分,進而得到以下二值向量
,其中
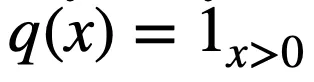
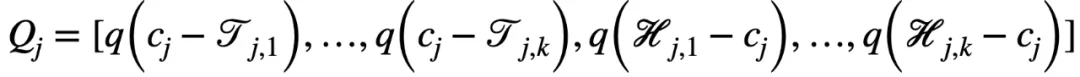
由于邏輯層的邊的連接是可以學習的,因此通過組合一個二值化層和一個邏輯層,模型可以實現自動選擇適當的邊界進行特征離散化(二值化),即以端到端的方式對特征進行二值化。例如:
- 當一個合取層節點連接了和,其表示區間
- 當一個析取層節點連接了和,其表示區間
梯度嫁接法
雖然連續值版本的邏輯層能夠使得整個 RRL 可導,但是在連續空間內搜索一個離散值解仍是一個巨大的挑戰。此外,邏輯激活函數的特性導致 RRL 在離散點處的梯度幾乎不含有用的信息,因此像 Straight-Through Estimator (STE)這類方法無法訓練 RRL。
為了高效地對不可導的 RRL 進行訓練,論文提出了一種新的基于梯度的離散模型訓練方法,梯度嫁接法。在植物嫁接中(如圖 3a 所示),一種植物的枝或芽作為接穗,而另一種植物的根或莖作為砧木,嫁接到一起,則得到了一種結合了二者優點的「新植物」。梯度嫁接法(Gradient Grafting)受植物嫁接方式的啟發,將損失函數對離散模型的輸出的梯度作為接穗,連續模型的輸出對模型參數的梯度作為砧木,進而構造出了一條完整的從損失函數到參數的反向傳播路徑(如圖 3b 所示)。令
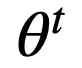
為 t 時刻的參數,
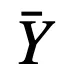
和
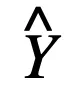
分別為離散模型和連續模型的輸出,則:
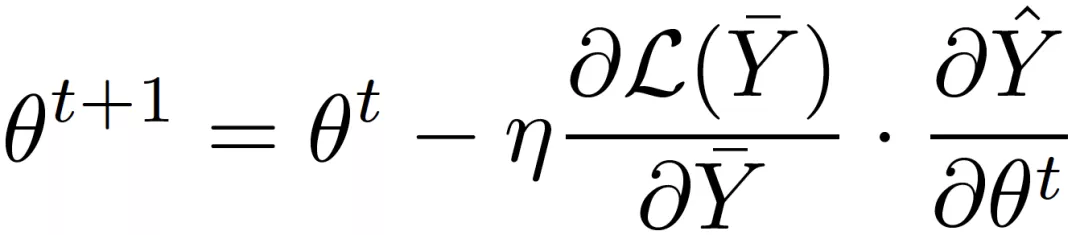
梯度嫁接法同時使用了參數空間中連續點和離散點處的梯度信息,并通過對兩者的拆分組合,實現了對離散模型的直接優化。
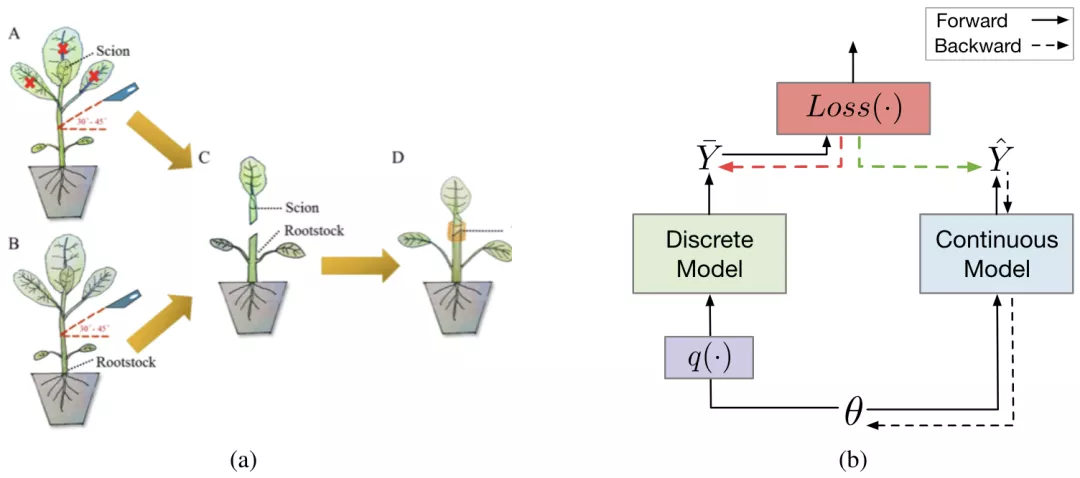
圖 3:(a) 植物嫁接示例(Chen et al., 2019)。(b) 梯度嫁接法的簡化計算圖。實線和虛線箭頭分別表示正向和反向傳播。綠色箭頭代表嫁接的梯度,它是紅色箭頭代表的梯度的一個拷貝。嫁接后,損失函數和參數之間存在一條反向傳播路徑。
實驗
論文通過實驗來評估 RRL 并回答了如下問題:
- RRL 的分類性能和模型復雜度如何?
- 相較于其他離散模型訓練方法,梯度嫁接法收斂如何?
- 改進后的邏輯激活函數的可擴展性如何?
作者在 9 個小規模數據集和 4 個大規模數據集上進行了實驗。這些數據集被廣泛用于測試模型的分類效果以及可解釋性。表 1 總結了這 13 個數據集的基本信息,可以看出,這 13 個數據集充分體現了數據的多樣性:實例數從 178 到 102944,類別數從 2 到 26,原始特征數從 4 到 4714。此外,數據集的特征類型和稀疏程度也各有差異。
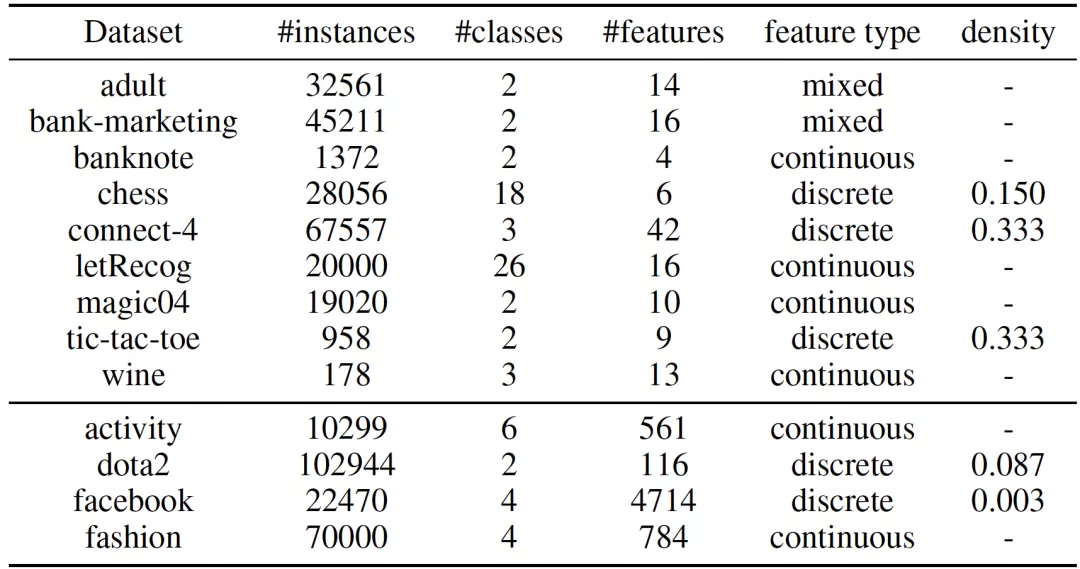
表 1:數據集統計信息
分類效果
論文將 RRL 的分類效果(F1 Score)與六個可解釋模型以及五個復雜模型進行了對比,結果如表 2 所示。其中 C4.5(Quinlan, 1993), CART(Breiman, 2017),Scalable Bayesian Rule Lists(SBRL)(Yang et al., 2017),Certifiably Optimal Rule Lists(CORELS)(Angelino et al., 2017)和 Concept Rule Sets(CRS)(Wang et al., 2020)是基于規則的模型,而 Logistic Regression(LR)(Kleinbaum et al., 2002) 是一個線性模型。這六個模型被認為是可解釋的。Piecewise Linear Neural Network(PLNN)(Chu et al., 2018), Support Vector Machines(SVM)(Scholkopf and Smola, 2001),Random Forest(Breiman, 2001),LightGBM(Ke et al., 2017)和 XGBoost(Chen and Guestrin, 2016)被認為是難以解釋的復雜模型。PLNN 是一類使用分段線性激活函數的多層邏輯感知機(Multilayer Perceptron, MLP)。RF,LightGBM 和 XGBoost 均為集成模型。
可以看出,RRL 顯著優于其他可解釋模型,只有兩個復雜模型,即 LightGBM 和 XGBoost 有著相當的結果。此外,RRL 在所有數據集上均取得了較好的結果,這也證明了 RRL 良好的可擴展性。
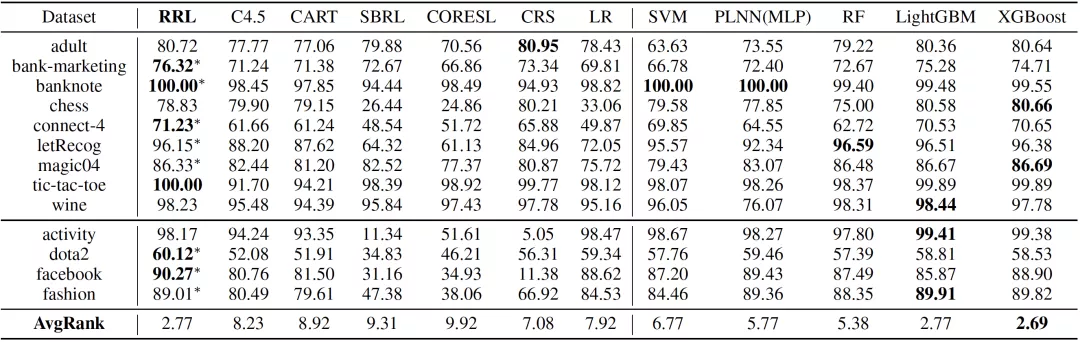
表 2:13 個數據集上各模型的分類效果(五折交叉驗證的 F1 Score)
模型復雜度
可解釋模型追求在確保準確率可接受的前提下,盡可能降低模型復雜度。如果模型分類效果太差,那么再低的模型復雜度也沒有意義。因此,從業人員真正關心的是模型分類效果與復雜度之間的關系。
考慮到存在規則復用的情況,論文使用邊的總數而不是規則總數來衡量基于規則的模型的復雜度(可解釋性)。RRL,CART,CRS 以及 XGBoost 的模型復雜度與模型分類效果之間的關系如圖 4 所示,其中橫軸為復雜度,縱軸為分類效果。可以看出,相比其他規則模型和集成模型,RRL 能夠更加高效地利用規則,即用更低的模型復雜度獲得更好的分類效果。結果還表明,通過參數設置,RRL 可以輕松地在模型復雜度和分類性能間進行權衡。
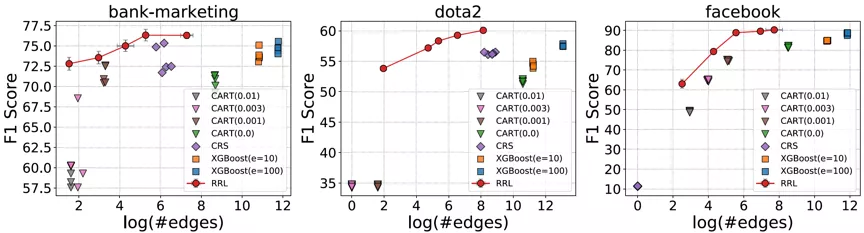
圖 4:RRL 與基線模型的模型復雜度與分類效果散點圖。
消融實驗
離散模型訓練方法
通過訓練結構相同的 RRL,作者將梯度嫁接法與 STE(Courbariaux et al., 2015, 2016),ProxQuant(Bai et al., 2018)以及 RB(Wang et al., 2020)這三類離散模型訓練方法進行了對比,訓練損失函數結果如圖 5 所示。由于 RRL 本身特殊的結構(即在離散點處的梯度具有極少的信息),只有使用梯度嫁接法訓練的 RRL 才能夠很好的收斂。
改進的邏輯激活函數
改進前后的邏輯激活函數的結果同樣在圖 5 中展示。可以看出,當處理大規模數據時,邏輯激活函數會發生梯度消失的問題,從而導致不收斂。而改進后的邏輯激活函數則克服了該問題。
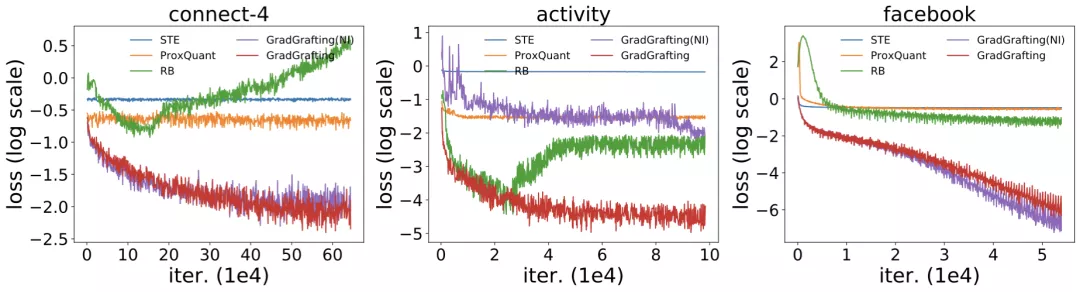
圖 5:梯度嫁接和另外三種離散模型訓練方法的訓練損失,以及使用改進前后的邏輯激活函數的訓練損失。
實例展示
權重分布
圖 6 展示的是不同正則項系數所對應的 RRL 線性層權重(規則重要度)的分布情況。當正則項系數比較小時,RRL 產生的規則比較復雜,數量較多。但從分布可以看出,大多數是權重絕對值較小的規則。因此,可以先去理解權重值較大的重要規則,當對模型整體和數據有了更好的認識后,再去理解權重較小的規則。而當正則項系數較大時,RRL 整體復雜度較低,則可以直接理解模型整體。
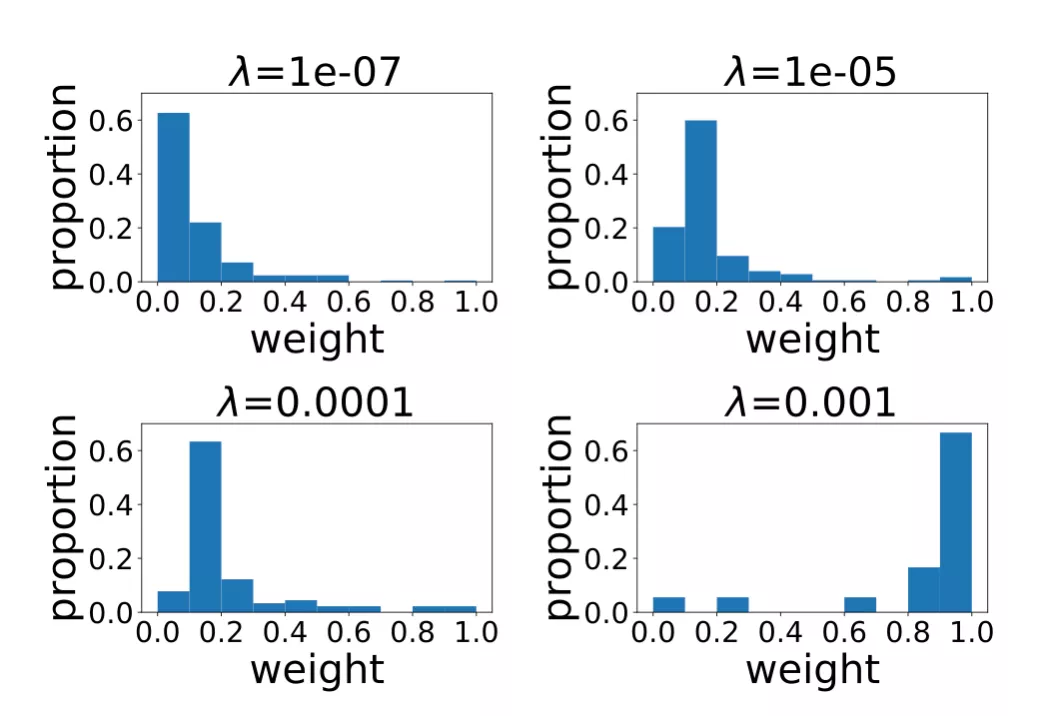
圖 6:不同正則項系數所對應的線性層權重分布。
具體規則
圖 7 為 bank-marketing 數據集所學到的部分規則,這些規則被用于預測用戶是否會在電話銷售中接受銀行的貸款。可以從這些規則中直觀看出哪些用戶狀態以及公司行為會對銷售結果產生影響,例如中年已婚的低存款用戶更可能接受貸款。銀行可以根據這些可解釋的規則來調整自己的營銷策略,以增加銷量。
雖然 RRL 并非專門設計用于圖像分類任務,但得益于其較好的可擴展性,RRL 仍可以通過可視化的方式為圖像分類任務提供直觀的解釋。圖 8 是對 fashion-mnist 圖像數據集上 RRL 所學到的規則的可視化。從中可以直觀地總結出模型的決策模式,例如通過袖子長短區分 T 恤和套頭衫。

圖 7:RRL 在 bank-marketing 數據集上學到的部分規則。
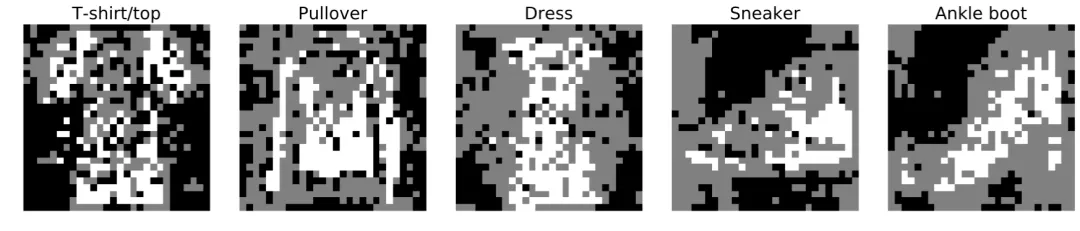
圖 8:RRL 在 fashion-mnist 圖像數據集上學到的規則的可視化。
總結
論文提出了一種新的可擴展分類器,規則表征學習器(RRL)。RRL 能夠通過自動學習可解釋的非模糊規則進行數據表征和分類。得益于自身的模型結構設計、梯度嫁接法以及改進版邏輯激活函數的使用,RRL 不僅有著較強的可擴展性,還能在模型復雜度較低的前提下獲得較好的分類效果。
RRL 的提出,不僅使得可解釋規則模型能夠適用于更大的數據規模和更廣的應用場景,還為從業人員提供了一個更好的在模型復雜度和分類效果之間權衡的方式。在未來工作中,把 RRL 拓展到非結構化數據上,如圖像和文本等,從而提升此類數據模型的可解釋性。