在上月于費(fèi)城舉辦的編程語言原理大會上，麻省理工學(xué)院(MIT)計(jì)算機(jī)科學(xué)與人工智能實(shí)驗(yàn)室(CSAIL)二年級博士生 Amanda Liu 表示，使用他們專為高性能計(jì)算而設(shè)計(jì)的新編程語言，可以很好地兼顧速度與正確性。此前人們普遍認(rèn)為，速度與可靠性存在不可避免的權(quán)衡。

據(jù)悉，Liu 與加州大學(xué)伯克利分校博士后 Gilbert Louis Bernstein、MIT 副教授 Adam Chlipala 和助理教授 Jonathan Ragan-Kelley 一道，描述了他們最近開發(fā)的“張量語言”(A Tensor Language)。

ATL 語言旨在產(chǎn)生一個數(shù)字或張量，所謂張量就向向量和矩陣的泛化。

向量是一維對象(通常由單獨(dú)的箭頭表示)，矩陣是相對臉熟的二維數(shù)字?jǐn)?shù)組。

而張量是 n 維數(shù)組，例如可用 3×3×3 的數(shù)組形式、或更高 / 更低的維度。

計(jì)算機(jī)算法或程序的全部意義，在于啟動特定的計(jì)算。不過想要實(shí)現(xiàn)目的，可用諸多不同的方式來編寫。正如該研究團(tuán)隊(duì)在即將發(fā)表的會議論文中所寫的那樣：

各種不同的代碼實(shí)現(xiàn)方式讓人眼花繚亂，某些方案的速度要快得多。

但鑒于高性能計(jì)算的資源開銷極其夸張，ATL 希望用更高效的方式來修改或重寫程序。

普通開發(fā)者習(xí)慣從最容易著手的地方開始編程，但這顯然沒有考慮到最佳的運(yùn)行效率，因而需要進(jìn)一步調(diào)整優(yōu)化。

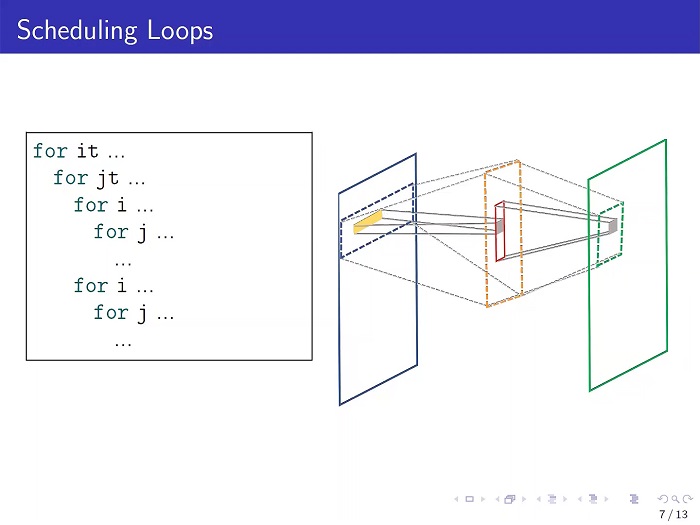
假設(shè)圖像由 100×100 的數(shù)字?jǐn)?shù)組表示，每個數(shù)字對應(yīng)一個像素，且希望獲得這些數(shù)字的均值。

這項(xiàng)工作可通過兩階計(jì)算完成，首先確定每行的平均值，然后獲取每列的平均值。

ATL 提供了一個相關(guān)的工具包 —— 計(jì)算機(jī)科學(xué)家稱之為“框架”—— 能夠展示如何將這兩個步驟轉(zhuǎn)換為更快的一步過程。

Liu 補(bǔ)充道：我們可借助所謂的“證明助手”(proof assistant)，來確保這種優(yōu)化的正確性。

有鑒于此，團(tuán)隊(duì)在現(xiàn)有的 Coq 語言的基礎(chǔ)上構(gòu)建了新語言。而其中包含的證明助手，具有以數(shù)學(xué)嚴(yán)謹(jǐn)?shù)姆绞阶C明其斷言的內(nèi)在能力。

不過在 MIT 團(tuán)隊(duì)看來，Coq 有另一個值得稱道的內(nèi)在特性 —— 用它編寫或適配的程序，是無法在無限循環(huán)中無止境地運(yùn)行的。

舉個例子，用 Java 編寫的程序，可能會發(fā)生這種狀況。我們運(yùn)行一個程序來得到一個單一的答案 —— 一個數(shù)字、或一個張量。

一個永不終止的程序，對我們說來毫無用處，但終止(terminate)是我們可使用 Coq 免費(fèi)獲得的一項(xiàng)特性。

只得一提的是，ATL 項(xiàng)目結(jié)合了 Ragan-Kelley 和 Chlipala 兩項(xiàng)研究的成果，前者長期持續(xù)關(guān)注著高性能計(jì)算背景下的算法優(yōu)化。

與此同時，Chlipala 更關(guān)注算法優(yōu)化的形式化(例如基于數(shù)學(xué)的驗(yàn)證)，但 ATL 是兩者都首次合作 —— Bernstein 和 Liu 與去年攜手，并產(chǎn)出了 ATL 這個成果。

據(jù)悉，ATL 是首個、也是迄今唯一一個具有正式驗(yàn)證優(yōu)化的張量語言。目前 ATL 仍處于原型階段，但研究團(tuán)隊(duì)已在許多小程序上展開了測試，可知其具有相當(dāng)光明的前景。

展望未來，他們的主要目標(biāo)之一是提升 ATL 的可擴(kuò)展性，以便它能夠用于我們在現(xiàn)實(shí)世界中看到的更大型的程序。

此前這些程序的優(yōu)化工作，通常需要人工來完成。除了總有臨時需要解決的問題、還總涉及反復(fù)實(shí)驗(yàn)，因而難免發(fā)生大量的錯誤。

好消息是，借助 ATL，我們有望遵循一種更具原則的方法來重寫這些程序 —— 且這么做更加容易，也更能保證程序的正確性。