作者 | 伊璉
一、前言
唯一不變的是變化,在擁抱它前,請事先探知、歸因、并充分準備。
在相對完善的指標體系建設背景下,我們需要通過指標以及指標波動的解讀來描述、追蹤、推動業務。當一個指標波動時,我們首先需要從業務視角判斷其波動是否異常,即異動檢測,其次判斷異常背后的原因是什么,即異動歸因。
歸因的方法有多種,這篇文章的重點是指標拆解,也是我們做業務分析時最常用到的方法。我們的目的是解放人力,將指標拆解實現自動化,一方面可以加快業務迭代速度,快速定位問題;另一方面可以對可能產生異動的維度進行全局量化,增強可比性,明確下一步的業務行動點的優先級。自動化異變歸因的目的是為了盡快判斷并抓住機遇,尋求以數據驅動作為燈塔指引業務航向。
二、目的
將目標指標定義為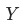 , 波動為
, 波動為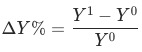 ,其中
,其中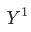 是當月的數據,
是當月的數據,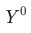 為上個月(同比/環比)的數據。
為上個月(同比/環比)的數據。
文章目的是為了研究組成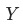 的集合
的集合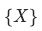 對于
對于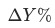 的貢獻:
的貢獻:
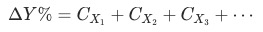 其中,
其中,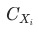 表示指標(或維度)
表示指標(或維度)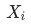 對于
對于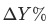
的貢獻度(contribution)。
另外,貢獻的拆解算法是根據組合方式不同決定,集合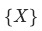 組成
組成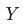 的方式包括:
的方式包括:
加法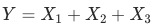 (例,各渠道uv加和)。
(例,各渠道uv加和)。
乘法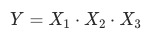 (例,已知rpm=cpc*ctr下,算出cpc、ctr分別對rpm的貢獻)。
(例,已知rpm=cpc*ctr下,算出cpc、ctr分別對rpm的貢獻)。
比率型指標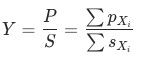 (例,各廣告計劃的cpf, 或者各個渠道的cpuv等)。
(例,各廣告計劃的cpf, 或者各個渠道的cpuv等)。
三、貢獻率的拆解方法
1. 加法拆解
已知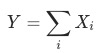 目標波動
目標波動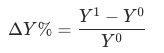 貢獻等于
貢獻等于
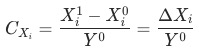 ,證明見附錄。
,證明見附錄。
舉例針對絕對值指標的維度拆解都是加法拆解。絕對量指標的同比/環比變化,就是各個分指標變化的加權求和,例如訪問uv總和等于各渠道uv加總, 那么總uv的變化下鉆貢獻率等于各渠道分別的變化除以上個月的總uv數。
2. 乘法拆解
已知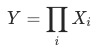 目標波動
目標波動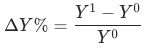 貢獻等于
貢獻等于
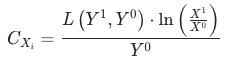 證明見附錄。
證明見附錄。
其中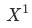 是當月的數據
是當月的數據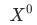 ,為上個月(同比/環比)的數據,
,為上個月(同比/環比)的數據,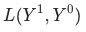
為平均對數權重:
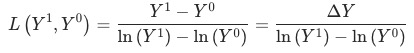
舉例 漏斗模型,借助用戶動線,拆解指標。
以全站商品詳情頁的瀏覽量(ipv)為例,其變動涉及流量、承接頁到商品詳情頁的轉化(uv-d轉化)、商品詳情頁用戶人均瀏覽量(人均pv),分別對應了用戶增長、搜推場景承接以及私域用戶活躍度等業務域或用戶行為指標。借此對全站ipv的構成鏈路進行靜態乘法拆解:
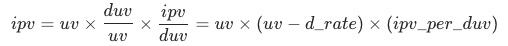
同時,我們可以計算各乘積因子對目標指標變化的貢獻率 ,衡量3個指標的重要性:
,衡量3個指標的重要性:
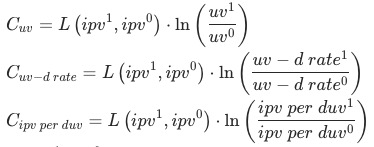
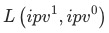 是平均對數權重,
是平均對數權重,
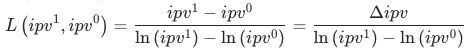
3. 比率型指標拆解
已知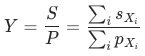 ,
,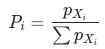 ,
,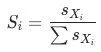 ,
,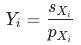 當分析比率指標進行維度下鉆,分項對整體的貢獻,受兩個因素影響。
當分析比率指標進行維度下鉆,分項對整體的貢獻,受兩個因素影響。
分項的相對數指標波動貢獻 ,即當期與基期的分項規模一致時,分項指標帶來的變化:分項的指標波動貢獻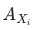 = 指標同比變化值 * 上期基數占比。
= 指標同比變化值 * 上期基數占比。
分項的結構變化 ,即當期與基期分項規模變化部分的指標變化:分項的結構變化
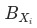 = 占比同比變化值 * (分項本期指標 - 整體上期指標 )。
= 占比同比變化值 * (分項本期指標 - 整體上期指標 )。
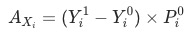 , 其中
, 其中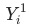 是當月的數據,
是當月的數據,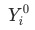 為上個月(同比/環比)的數據。
為上個月(同比/環比)的數據。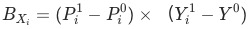
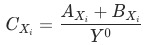 , 證明見附錄。
, 證明見附錄。
舉例 以承接頁到商品詳情頁的轉化率(uv-d轉化率rate)為例,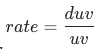 ,流量渠道可分為付費、免費、自然、其他,每種渠道的uv-d轉化率為
,流量渠道可分為付費、免費、自然、其他,每種渠道的uv-d轉化率為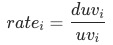 ,各渠道的商詳頁訪問人數(duv)占比用
,各渠道的商詳頁訪問人數(duv)占比用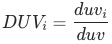 表示,各渠道人數(uv)占比用
表示,各渠道人數(uv)占比用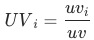 ,如果uv-d轉化率同比下跌,我們想定位出哪個渠道出現了問題;各渠道的貢獻
,如果uv-d轉化率同比下跌,我們想定位出哪個渠道出現了問題;各渠道的貢獻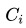 是怎么樣計算為:
是怎么樣計算為:
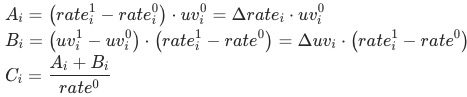
4. 實例應用
根據上文提到的不同指標的計算方法,支持全類型指標下鉆求貢獻的場景, 可根據先驗業務輸入搭建多層的歸因邏輯模型, 層層下鉆,最終將指標波動定位。
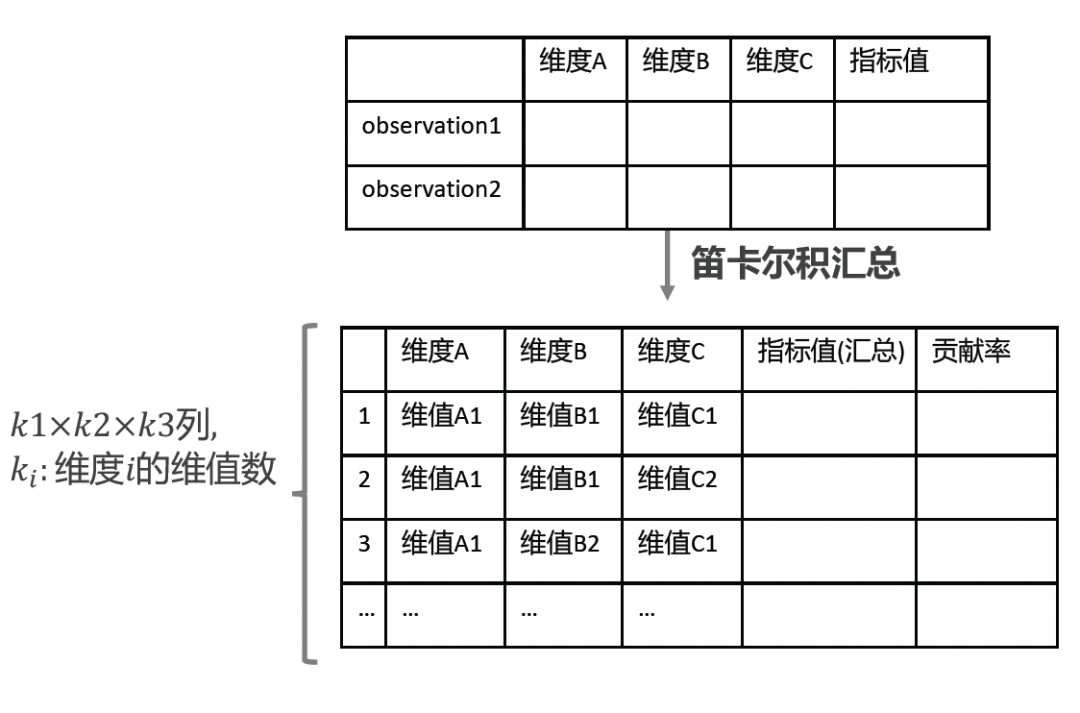
圖二:計算貢獻率之后的數據結果樣式
以2011年某日ipv同比下跌的異動分析為例:
第一層拆解,借助用戶動線,將存在異動變化的指標ipv構成鏈路進行乘法拆解,如下:
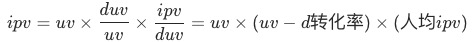
這里幫助我們定位到可能導致指標異動的關鍵節點,這有助于我們將問題定位到具體業務域,例如是uv的問題,轉化的問題,還是人均ipv的問題?
第二層拆解,對關鍵節點處的多個維度進行下鉆,將問題定位到某些維度的某些水平上,同時避免陷入辛普森悖論等陷阱,這有助于我們形成具體業務域有所行動, 例如如果是轉化的問題,究竟是哪個渠道的轉化減少了?
下圖“異動分析拆解流程圖”是根據先驗的業務輸入搭建的歸因模型,根據其框架得以進行貢獻率拆解與問題定位:
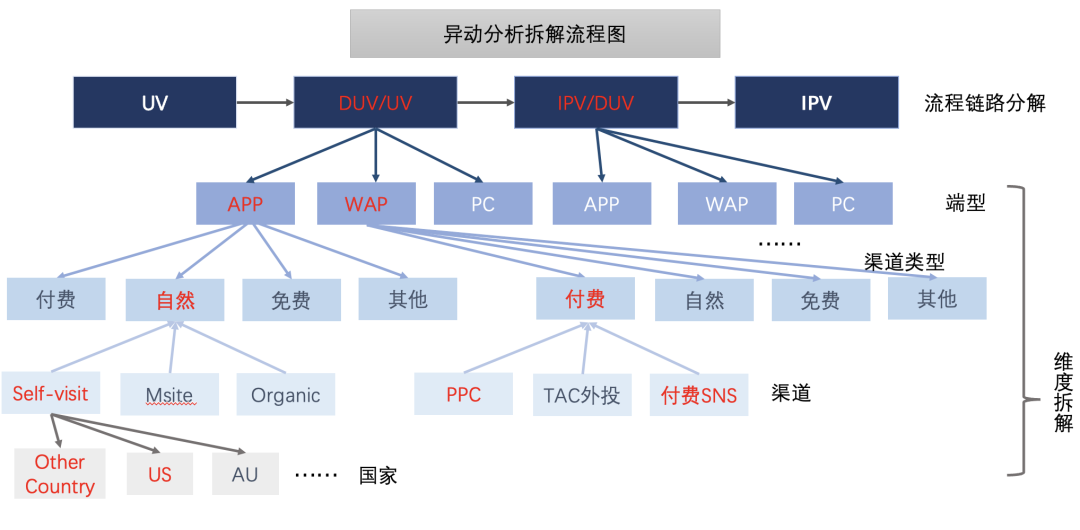
圖三:指標拆解逐層歸因
紅色表示的鏈路指標或維度代表對總值下跌貢獻率較大,經過一層一層的拆解定位到app端自然流量中轉化的降低導致總轉化下降。
基于流量跨端調控以及流量預算減投的業務背景,我們現將對ipv貢獻最大的uv/duv根據端型、流量渠道類型、流量渠道、國家四個維度進行貢獻率拆解。
在本實例中,通過本文對貢獻率拆解方法與業務人工看數得到的問題定位基本一致,該方法可以實現異動貢獻率量化與提效的目的,具體核心結論如下:
結論一 (第一層拆解)ipv下降主要影響因素是uv-d轉化率的波動。
結論二 (第二層拆解)uv-d比率的波動主要由APP端與WAP端導致,兩種端型貢獻持平。
結論三 (第三/四層拆解)APP端的自然流量和wap端的付費流量是uv-d總比率波動的主要貢獻維度。
結論四 (第五層拆解)APP端self-visit中美國對uv-d比率的波動貢獻較大。
通過建立多層歸因下鉆維度模型, 用自動化的方式層層剝析,從而能盡求完善且正確的歸因到某個維度,從而節省人力,提高準確和科學性。
四、多層下鉆歸因方案—決策樹
本節重點在拆解求出貢獻率之后,如何探查異動。我們已經把不同維度下,每個維值的貢獻率求出, 下一步的目的是求出貢獻最大(有異動的)的維度維值組合,測三種拆解方案,包括逐層下鉆(同上文3.4的下鉆方式)、多層同步下鉆、 決策樹模型,發現決策樹模型效果最好。這里決策樹輸入為不同的維值組合,輸出為貢獻率,做的是回歸預測。
主要做法是求貢獻率的熵,找到信息增益最高切割方法。這里自然而然想到決策樹模型,通過貪心算法,切割數據空間, 找到貢獻率絕對值最高的維度組合空間。圖四長方形整體表示數據空間,表示兩個維度,其下角標表示維度下的維值。下圖具象的看出通過不同維值的組合,把數據空間切割成不同塊,用不同的顏色代表。
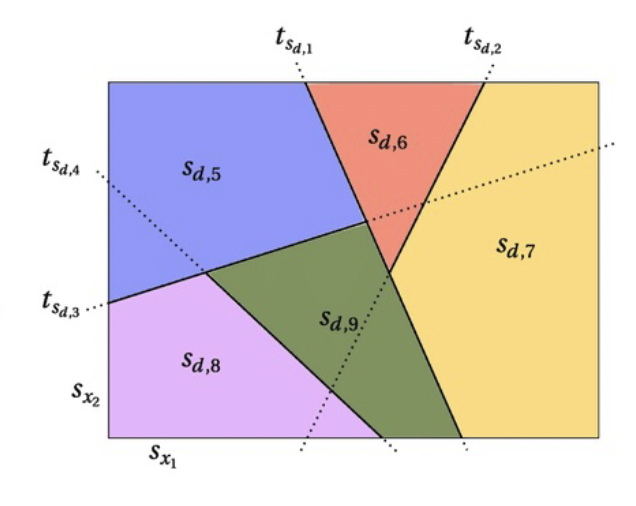
圖四:決策樹對數據空間的切割可視化
1. 剪枝
決策樹存在過擬合的問題, 為了解決這個問題,我們決定了剪枝的方法,采用后剪枝(Post-pruning)。后剪枝就是先把整顆決策樹構造完畢,然后自底向上的對非葉結點進行考察,若將該結點對應的子樹換為葉結點能夠帶來泛華性能的提升,則把該子樹替換為葉結點。
后剪枝的方法包括:REP-錯誤率降低剪枝, PEP-悲觀剪枝, CCP-代價復雜度剪枝, MEP-最小錯誤剪枝。
我們借鑒了CCP—代價復雜度的方法。選擇節點表面誤差率增益值大的層級的非葉子節點,刪除該非葉子節點的左右子節點,若有多個非葉子節點的表面誤差率增益值相同小,則選擇非葉子節點中子節點數最多的非葉子節點進行剪枝。這個算法的參數為
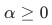 , 表示算法的復雜度:
, 表示算法的復雜度: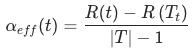
其中,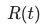 表示的是結點
表示的是結點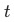 的方差(近似加權熵的概念:impurity,下文都泛稱為熵,計算公式),
的方差(近似加權熵的概念:impurity,下文都泛稱為熵,計算公式),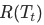 是結點
是結點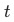 的子樹
的子樹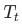 的熵的總和,
的熵的總和,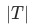 為決策樹結點個數 。
為決策樹結點個數 。
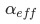 高,表示結點
高,表示結點 往下分的信息增益高。圖五表示異動維數的個數與決策樹層結點熵的平均數的關系:以黃線為例,
當異動的維數為2時,決策樹在第二層的熵最高,從第二層往后,再往下分熵越小,信息增益少,過擬合明顯。從折線明顯看到,熵的拐點在第二層,決策樹最大深度等于2。
往下分的信息增益高。圖五表示異動維數的個數與決策樹層結點熵的平均數的關系:以黃線為例,
當異動的維數為2時,決策樹在第二層的熵最高,從第二層往后,再往下分熵越小,信息增益少,過擬合明顯。從折線明顯看到,熵的拐點在第二層,決策樹最大深度等于2。
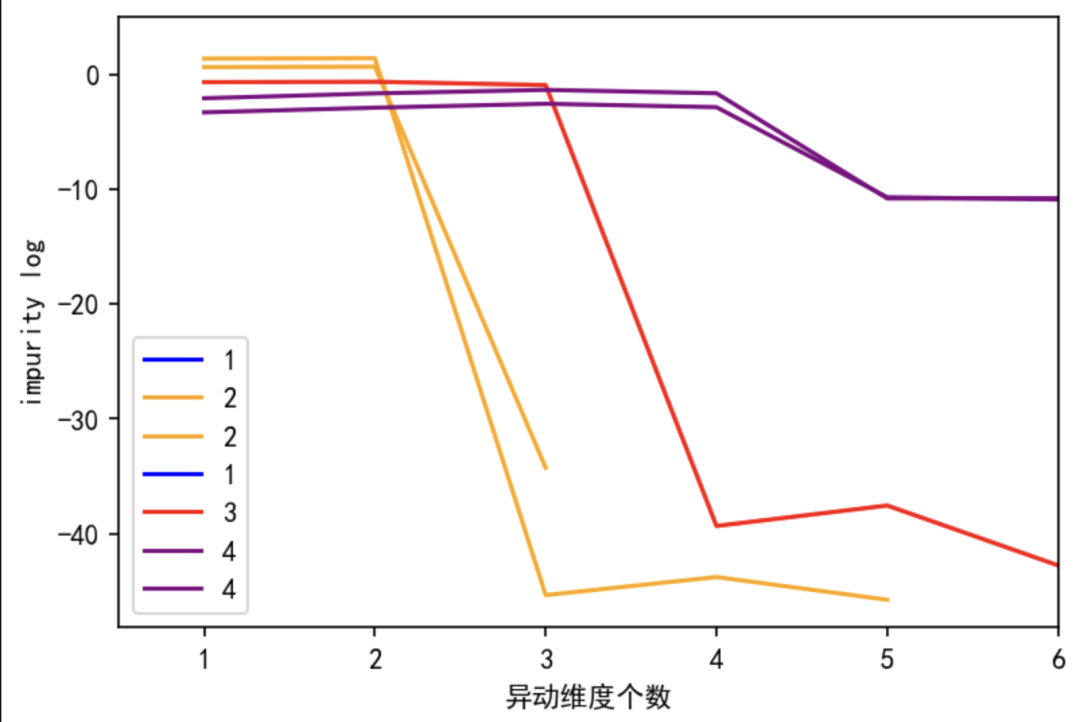
圖五:異動維數的個數與結點方差(熵)的關系
我們從圖五的事例啟發,按照CPP的方法, 找躍層增益較大的“拐點”,找到合適的
進行剪枝。
五、模型表現
1. 模擬數據
我們模擬的維度和維值如下,共4個維度(兩兩獨立), 涉及維值共40個,4個維度維值組合(笛卡爾積 31*2*3*4=744)共744個。模擬的時間對比為月環比,模擬指標為廣告消耗。
維度字段 | country_cn_name | is_free | terminal_type_cd | imps_cnt_bins |
維度 | 國家 | 渠道 | 端型 | 曝光檔位 |
維值數 | 31 | 2 | 3 | 4 |
舉例 | 馬來西亞 | 免費 | WAP | (-1.0, 0.0] |
無異動數據:用白噪音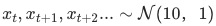 模擬無異動的維度組合的時間序列,見圖六:
模擬無異動的維度組合的時間序列,見圖六:
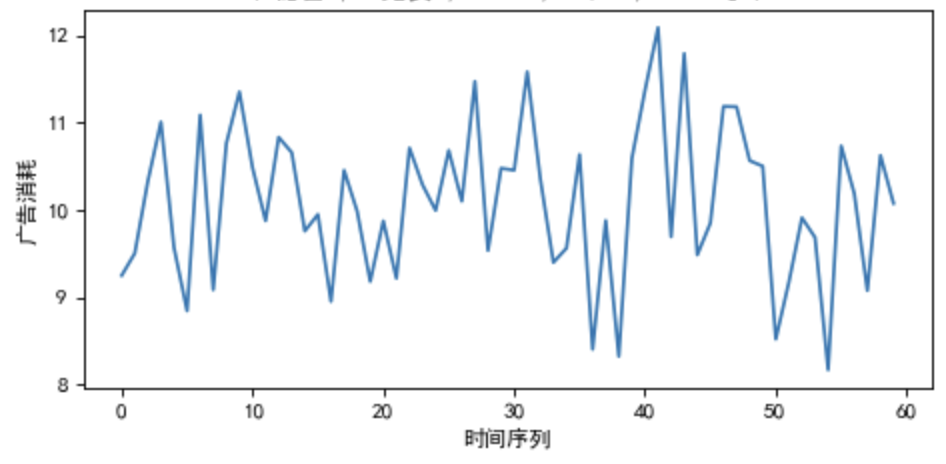
圖六:無異動的時間序列
有異動數據:用隨機游走的累積和來模擬異動,公式如下,見圖七:
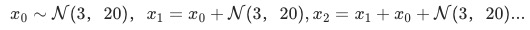
圖七(a):有異動的時間序列1
2. 模型評估
在上圖四個維度(國家、渠道、端型、曝光檔位),指定特定的維度和維值在3月有異動,通過決策樹模型,測試是否找到正確異動點。模擬case考慮的主要是可能存在異動的真實情況:
- 某個PID數據錄入異常,會影響單維度的異動(僅那個PID的數據)。
- 某個渠道且某個端型的減投,會影響多個維度組合的異動。由于指標異動涉及的業務繁雜,不同團隊在不同方向的優化,影響到不同的維值組合。
例一:異動維度在兩處
異動維值組合:
a. 國家=伊拉克, 渠道=免費, 端型='WAP', 曝光檔位=[5:100]
b. 國家=法國, 渠道=免費, 端型='PC', 曝光檔位=[0:5]
將貢獻度算出,數據輸入決策樹模型, 結果見圖八,可以看出決策樹精確的找到異動的數據(共精確找到7個維值,共8個), 且這兩組標紅數據對于異動的貢獻絕對值最大。我們自定義樹結構找父節點的方法,自動剪掉冗余分支,只截取重點枝干呈現。
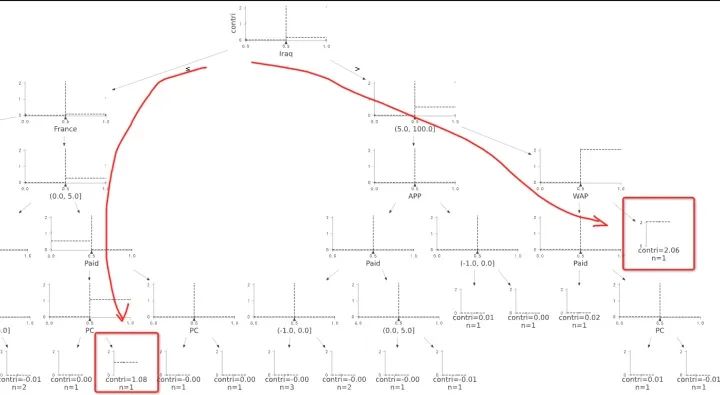
圖八:決策樹結果呈現
特征重要性也符合預期:
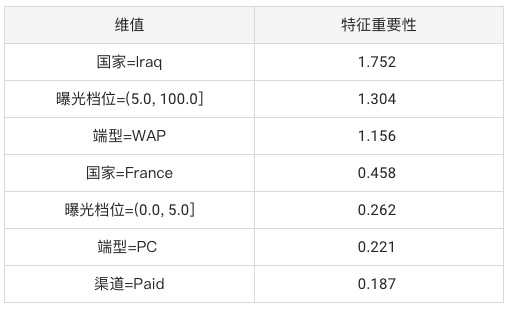
例二:異動維度在一處,只異動一個維度在付費上
異動維值組合:a. 渠道=付費
通過剪枝,模型成功找到一維信息,避免提供太多噪音令用戶混淆。
更多
表一包含更多維值組合案例, 以及模型表現,包括F1-score,模型輸出的結果,和特征重要性。已探索11個案例,平均F1-score達到91.9%。
下面的數量是異動的維值個數:
| Positive Prediction | Negative PredictionPositive Class | True Positive (TP) 34 | False Negative (FN) 6Negative Class | False Positive (FP) 0 | True Negative (TN) 0
最后結果:
Precision = 34 / (34 + 0) = 100%Recall = 34 / (34 + 6) = 85% F-1 Score Overall = 91.9%
異動維值組合(label/y_true) | F1-Score | 模型結果1:模型輸出(結果可視化展現,自動剪掉冗余分支,只截取貢獻高的枝干呈現) | 模型結果2:特征重要性 | |
1 | APP | 100% | APP ->貢獻率為 0.58 | APP: 0.790 |
2 | 法國 | 100% | 法國 ->貢獻率為 0.84 | 法國 : 0.542; |
3 | 付費 | 100% | 付費 ->貢獻率為 0.43 | 付費 : 0.570; |
4 | 法國&付費 | 100% | 法國 -> 付費 -> 貢獻率為 0.81 | 法國 : 1.988; 付費 : 1.019; |
5 | 法國&APP | 100% | 法國 -> APP -> 貢獻率為 0.84 | 法國 : 1.895;APP: 1.360 |
6 | APP&付費 | 100% | APP -> 付費 -> 貢獻率為 0.41 | APP: 1.591付費 : 1.203; |
7 | APP&付費&法國 | 100% | 法國 -> APP -> 付費 ->貢獻率為 0.88 | 法國 : 1.944;APP: 1.374;付費 : 1.047; |
8 | APP&付費&法國&(5.0, 100.0] | 100% | 法國 -> (5.0, 100.0] -> APP -> 付費 ->貢獻率為 0.90 | 法國 : 1.836;APP: 1.469;(5.0, 100.0]: 1.369;付費 : 1.302; |
9 | APP&付費&法國&(5.0, 100.0]orPC&免費&伊拉克 | 83% | 非伊拉克 -> 法國 -> (5.0, 100.0] ->貢獻率為 0.14 伊拉克 -> PC -> 非付費 ->貢獻率為 0.87 | 伊拉克: 1.610;PC : 1.027;付費 : 0.772;法國 : 0.062;(5.0, 100.0]: 0.052; |
10 | APP&付費&法國orPC&免費&伊拉克&(5.0, 100.0] | 83% | 非法國 -> 伊拉克 -> (5.0, 100.0] ->貢獻率為 0.14 法國 -> APP -> 非免費 ->貢獻率為 0.87 | 法國 : 1.559;APP: 1.101;免費 : 0.839;伊拉克: 0.064;(5.0, 100.0]: 0.058;PC : 0.000 |
11 | APP&付費&法國orPC&免費&伊拉克&(5.0, 100.0]or美國&免費&APP | 88% | 非美國-> 非法國-> 伊拉克-> (5.0, 100.0]->貢獻率為 0.14 非美國-> 法國-> APP-> 付費->貢獻率為 0.84 美國-> APP-> 非付費->貢獻率為 0.84 | APP : 1.218 美國 : 0.936 付費 : 0.907 法國 : 0.863 伊拉克 : 0.035 (5.0, 100.0]: 0.033 土耳其 : 0.000 |
六、局限
但此方法論還是有其局限性的,主要在于歸因變量(下鉆維度)有限,大多數情況下是按照業務的理解和先驗的經驗來判斷。本方法只能識別業務已經認可的拆解維度和鏈路定位,拆解到的指標或維度都是已知業務系統內的指標,諸如工程問題、宏觀政策等因素難以識別,需要輔以定性分析。具體來說,我們看到pv下降,下意識要去從渠道下鉆,主要原因是我們因為渠道作為變量,是和pv數有正向(或者因果)關系的。舉個極端的例子,有可能是服務器的故障,導致全平臺的pv下跌。這樣的潛在變量,如果和常用下鉆變量彼此相互獨立的條件下,是無法通過此方法論探查得到的。我們后續的工作將重點放在對相互獨立的指標和相關事件的角度做進一步更全面的因果推斷算法研究。
七、技術產品化
我們工作中月報和周報中通常分析的方法與此類似,不同的是,因為人力有限,數據龐雜,往往下鉆維度和層數局限,比率類型指標不知道如何下鉆等等,導致科學性和嚴謹性很難保持。這套方法實現了自動化,保證計算的準確性,節省人日。我們將此技術沉淀在內部數據產品“象數”上。象數中心是ICBU數據驅動的基石產品,是集數據資產定義與管理、A/B實驗、洞察分析于一體的數據平臺。它提供的核心價值在于好找、敢用、持續保鮮的數據資產,大規模、可信的端到端實驗能力,以及因果、異動等智能化的分析工具。

八、附錄
證明 加法貢獻算法
已知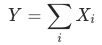 貢獻等于
貢獻等于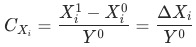 ,
,
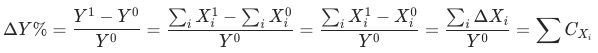
證明 乘法貢獻算法
已知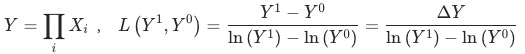 ,
,
貢獻等于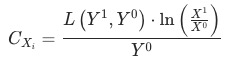 ,目標波動
,目標波動
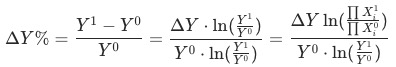
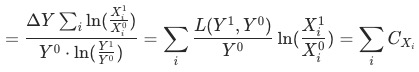
證明 比率貢獻算法
已知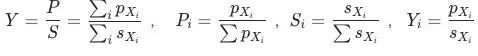
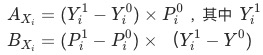 , 其中
, 其中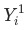 是當月的數據,
是當月的數據,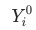 為上個月(同比/環比)的數據。
為上個月(同比/環比)的數據。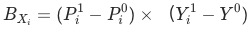 貢獻等于
貢獻等于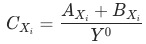
算法得到的貢獻率依舊相互獨立,符合MECE原則,且通過分別觀測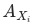 和
和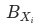
有助于我們避開辛普森悖論帶來的陷阱。

備注: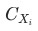 符合mece原則證明:相互獨立:
符合mece原則證明:相互獨立: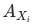 和
和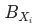 的計算公式中不涉及其他分項的完全窮盡。
的計算公式中不涉及其他分項的完全窮盡。
參考
Ang, Beng W., F. Q. Zhang, and Ki-Hong Choi. "Factorizing changes in energy and environmental indicators through decomposition." Energy 23.6 (1998): 489-495.
Ang B W . The LMDI approach to decomposition analysis: a practical guide[J]. Energy Policy, 2005, 33(7):867-871.
《波動解讀—指標拆解的加減乘除雙因素》https://zhuanlan.zhihu.com/p/412117828