使用Python從頭開始手寫回歸樹
為了簡單起見這里將使用遞歸來創建樹節點,雖然遞歸不是一個完美的實現,但是對于解釋原理他是最直觀的。
首先導入庫
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
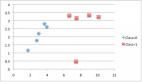
首先需要創建訓練數據,我們的數據將具有獨立變量(x)和一個相關的變量(y),并使用numpy在相關值中添加高斯噪聲,可以用數學表達為
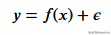
這里的 是噪聲。代碼如下所示。
def f(x):
mu, sigma = 0, 1.5
return -x**2 + x + 5 + np.random.normal(mu, sigma, 1)
num_points = 300
np.random.seed(1)
x = np.random.uniform(-2, 5, num_points)
y = np.array( [f(i) for i in x] )
plt.scatter(x, y, s = 5)
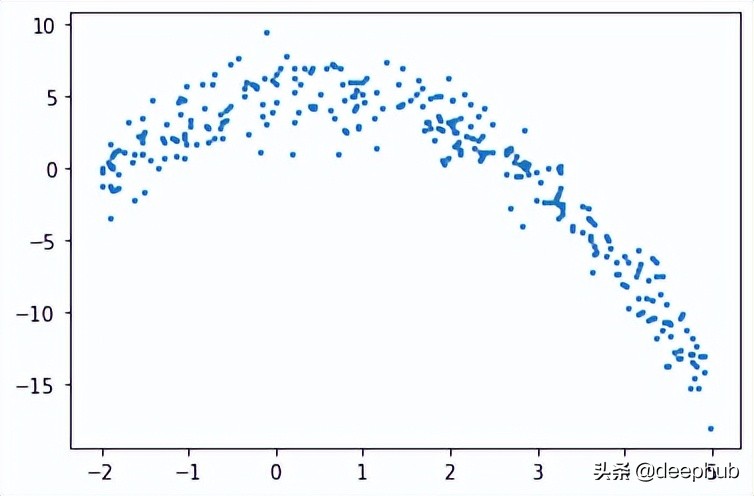
回歸樹
在回歸樹中是通過創建一個多個節點的樹來預測數值數據的。 下圖展示了一個回歸樹的樹結構示例,其中每個節點都有其用于劃分數據的閾值。
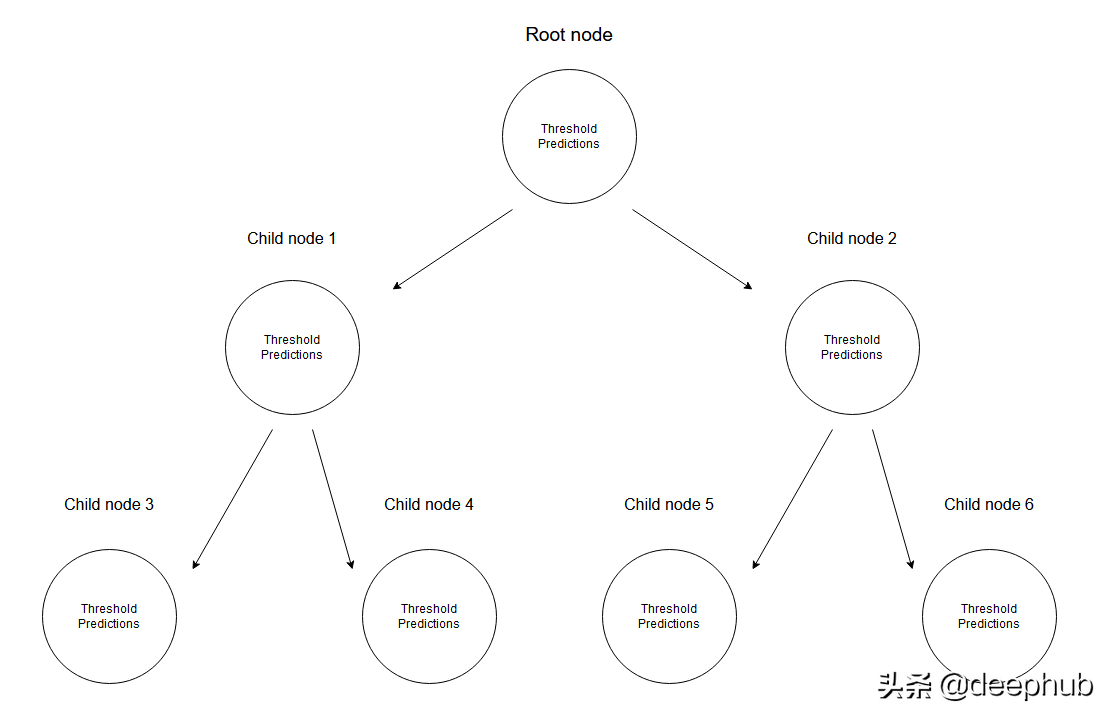
給定一組數據,輸入值將通過相應的規格達到葉子節點。 達到節點M的所有輸入值可以用X的子集表示。從數學上講,讓我們用一個函數表達此情況,如果給定的輸入值達到節點M,則可以給出1個,否則為0。
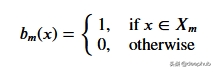
找到分裂數據的閾值:通過在每個步驟中選擇2個連續點并計算其平均值來迭代訓練數據。 計算的平均值將數據分為兩個的閾值。
首先讓我們考慮隨機閾值以演示任何給定的情況。
threshold = 1.5
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
plt.scatter(x, y, s = 5, label = 'Data')
plt.plot([threshold]*2, [-16, 10], 'b--', label = 'Threshold line')
plt.plot([-2, threshold], [low.mean()]*2, 'r--', label = 'Left child prediction line')
plt.plot([threshold, 5], [high.mean()]*2, 'r--', label = 'Right child prediction line')
plt.plot([-2, 5], [y.mean()]*2, 'g--', label = 'Node prediction line')
plt.legend()
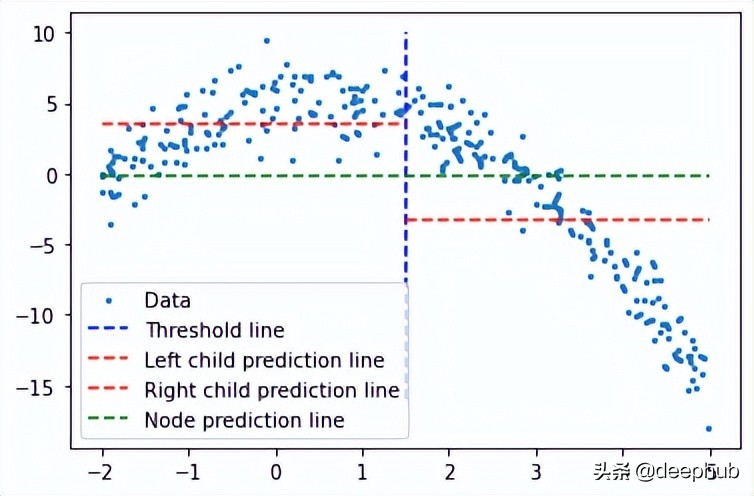
藍色垂直線表示單個閾值,我們假設它是任意兩點的均值,并稍后將其用于劃分數據。
我們對這個問題的第一個預測是所有訓練數據(y軸)的平均值(綠色水平線)。而兩條紅線是要創建的子節點的預測。
很明顯這些平均值都不能很好地代表我們的數據,但它們的差異也是很明顯的:主節點預測(綠線)得到所有訓練數據的均值,我們將其分為2個子節點,這2個子節點有自己的預測(紅線)。與綠線相比這2個子節點更好地代表了它們對應的訓練數據。回歸樹就是將不斷地將數據分成2個部分——從每個節點創建2個子節點,直到達到給定的停止值(這是一個節點所能擁有的最小數據量)。它會提前停止樹的構建過程,我們將其稱為預修剪樹。
為什么會有早停的機制?如果我們要繼續進行分配直到節點只有一個值是,這創建一個過度擬合的方案,每個訓練數據都只能預測自己。
說明:當模型完成時,它不會使用根節點或任何中間節點來預測任何值;它將使用回歸樹的葉子(這將是樹的最后一個節點)進行預測。
為了得到最能代表給定閾值數據的閾值,我們使用殘差平方和。它可以在數學上定義為
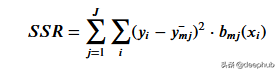
讓我們看看這一步是如何工作的。
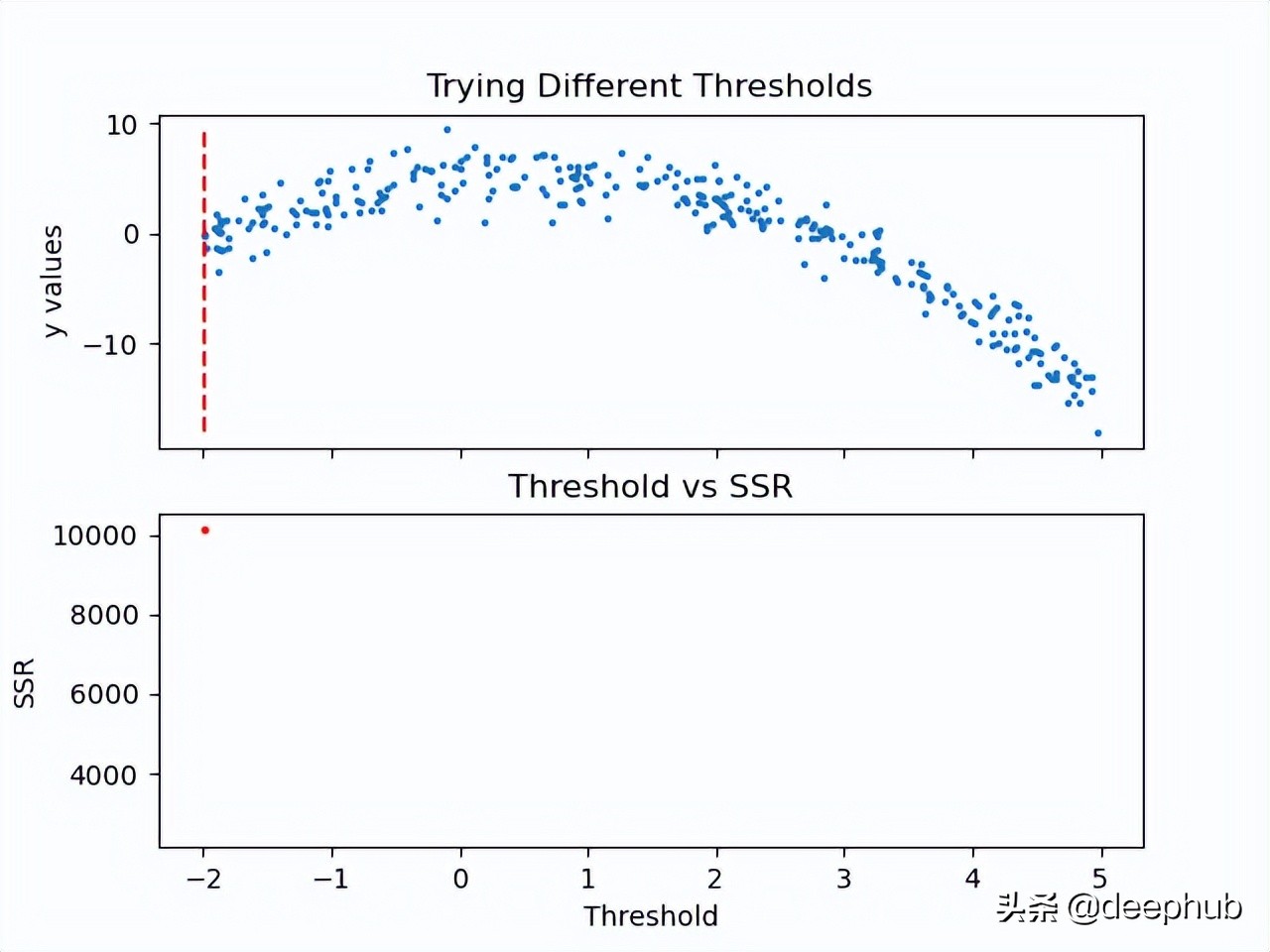
既然計算了閾值的SSR值,那么可以采用具有最小SSR值的閾值。使用該閾值將訓練數據分為兩個(低和高部分),其中其中低部分將用于創建左子節點,高部分將用于創建右子節點。
def SSR(r, y):
return np.sum( (r - y)**2 )
SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
guess_low = low.mean()
guess_high = high.mean()
SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)
print('Minimum residual is: {:.2f}'.format(min(SSRs)))
print('Corresponding threshold value is: {:.4f}'.format(thresholds[SSRs.index(min(SSRs))]))

在進入下一步之前,我將使用pandas創建一個df,并創建一個用于尋找最佳閾值的方法。所有這些步驟都可以在沒有pandas的情況下完成,這里使用他是因為比較方便。
df = pd.DataFrame(zip(x, y.squeeze()), columns = ['x', 'y'])
def find_threshold(df, plot = False):
SSRs, thresholds = [], []
for i in range(len(df) - 1):
threshold = df.x[i:i+2].mean()
low = df[(df.x <= threshold)]
high = df[(df.x > threshold)]
guess_low = low.y.mean()
guess_high = high.y.mean()
SSRs.append(SSR(low.y.to_numpy(), guess_low) + SSR(high.y.to_numpy(), guess_high))
thresholds.append(threshold)
if plot:
plt.scatter(thresholds, SSRs, s = 3)
plt.show()
return thresholds[SSRs.index(min(SSRs))]
創建子節點
在將數據分成兩個部分后就可以為低值和高值找到單獨的閾值。需要注意的是這里要增加一個停止條件;因為對于每個節點,屬于該節點的數據集中的點會變少,所以我們為每個節點定義了最小數據點數量。如果不這樣做,每個節點將只使用一個訓練值進行預測,會導致過擬合。
可以遞歸地創建節點,我們定義了一個名為TreeNode的類,它將存儲節點應該存儲的每一個值。使用這個類我們首先創建根,同時計算它的閾值和預測值。然后遞歸地創建它的子節點,其中每個子節點類都存儲在父類的left或right屬性中。
在下面的create_nodes方法中,首先將給定的df分成兩部分。然后檢查是否有足夠的數據單獨創建左右節點。如果(對于其中任何一個)有足夠的數據點,我們計算閾值并使用它創建一個子節點,用這個新節點作為樹再次調用create_nodes方法。
class TreeNode():
def __init__(self, threshold, pred):
self.threshold = threshold
self.pred = pred
self.left = None
self.right = None
def create_nodes(tree, df, stop):
low = df[df.x <= tree.threshold]
high = df[df.x > tree.threshold]
if len(low) > stop:
threshold = find_threshold(low)
tree.left = TreeNode(threshold, low.y.mean())
create_nodes(tree.left, low, stop)
if len(high) > stop:
threshold = find_threshold(high)
tree.right = TreeNode(threshold, high.y.mean())
create_nodes(tree.right, high, stop)
threshold = find_threshold(df)
tree = TreeNode(threshold, df.y.mean())
create_nodes(tree, df, 5)
這個方法在第一棵樹上進行了修改,因為它不需要返回任何東西。雖然遞歸函數通常不是這樣寫的(不返回),但因為不需要返回值,所以當沒有激活if語句時,不做任何操作。
在完成后可以檢查此樹結構,查看它是否創建了一些可以擬合數據的節點。 這里將手動選擇第一個節點及其對根閾值的預測。
plt.scatter(x, y, s = 0.5, label = 'Data')
plt.plot([tree.threshold]*2, [-16, 10], 'r--',
label = 'Root threshold')
plt.plot([tree.right.threshold]*2, [-16, 10], 'g--',
label = 'Right node threshold')
plt.plot([tree.threshold, tree.right.threshold],
[tree.right.left.pred]*2,
'g', label = 'Right node prediction')
plt.plot([tree.left.threshold]*2, [-16, 10], 'm--',
label = 'Left node threshold')
plt.plot([tree.left.threshold, tree.threshold],
[tree.left.right.pred]*2,
'm', label = 'Left node prediction')
plt.plot([tree.left.left.threshold]*2, [-16, 10], 'k--',
label = 'Second Left node threshold')
plt.legend()
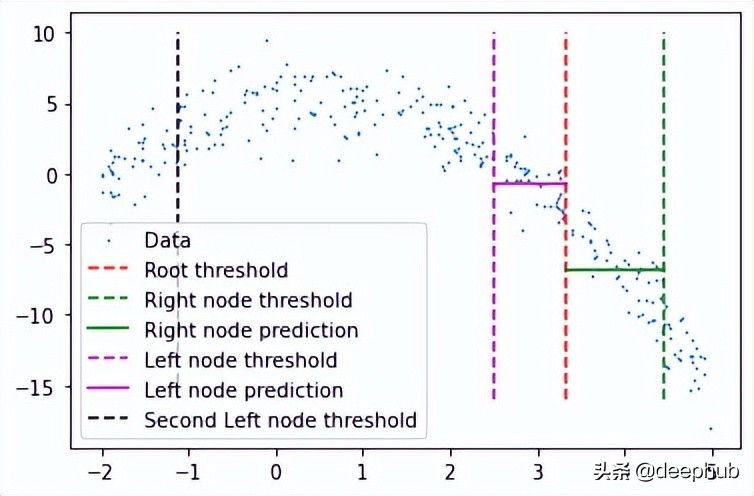
這里看到了兩個預測:
- 第一個左節點對高值的預測(高于其閾值)
- 第一個右節點對低值(低于其閾值)的預測
這里我手動剪切了預測線的寬度,因為如果給定的x值達到了這些節點中的任何一個,則將以屬于該節點的所有x值的平均值表示,這也意味著沒有其他x值參與 在該節點的預測中(希望有意義)。
這種樹形結構遠不止兩個節點那么簡單,所以我們可以通過如下調用它的子節點來檢查一個特定的葉子節點。
tree.left.right.left.left
這當然意味著這里有一個向下4個子結點長的分支,但它可以在樹的另一個分支上深入得多。
預測
我們可以創建一個預測方法來預測任何給定的值。
def predict(x):
curr_node = tree
result = None
while True:
if x <= curr_node.threshold:
if curr_node.left: curr_node = curr_node.left
else:
break
elif x > curr_node.threshold:
if curr_node.right: curr_node = curr_node.right
else:
break
return curr_node.pred
預測方法做的是沿著樹向下,通過比較我們的輸入和每個葉子的閾值。如果輸入值大于閾值,則轉到右葉,如果小于閾值,則轉到左葉,以此類推,直到到達任何底部葉子節點。然后使用該節點自身的預測值進行預測,并與其閾值進行最后的比較。
使用x = 3進行測試(在創建數據時,可以使用上面所寫的函數計算實際值。-3**2+3+5 = -1,這是期望值),我們得到:
predict(3)
# -1.23741
計算誤差
這里用相對平方誤差驗證數據
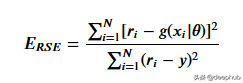
def RSE(y, g):
return sum(np.square(y - g)) / sum(np.square(y - 1 / len(y)*sum(y)))
x_val = np.random.uniform(-2, 5, 50)
y_val = np.array( [f(i) for i in x_val] ).squeeze()
tr_preds = np.array( [predict(i) for i in df.x] )
val_preds = np.array( [predict(i) for i in x_val] )
print('Training error: {:.4f}'.format(RSE(df.y, tr_preds)))
print('Validation error: {:.4f}'.format(RSE(y_val, val_preds)))
可以看到誤差并不大,結果如下

概括的步驟

更深入的模型
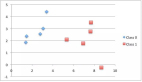
一個更適合回歸樹模型的數據:因為我們的數據是多項式生成的數據,所以使用多項式回歸模型可以更好地擬合。我們更換一下訓練數據,把新函數設為
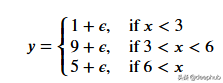
def f(x):
mu, sigma = 0, 0.5
if x < 3: return 1 + np.random.normal(mu, sigma, 1)
elif x >= 3 and x < 6: return 9 + np.random.normal(mu, sigma, 1)
elif x >= 6: return 5 + np.random.normal(mu, sigma, 1)
np.random.seed(1)
x = np.random.uniform(0, 10, num_points)
y = np.array( [f(i) for i in x] )
plt.scatter(x, y, s = 5)
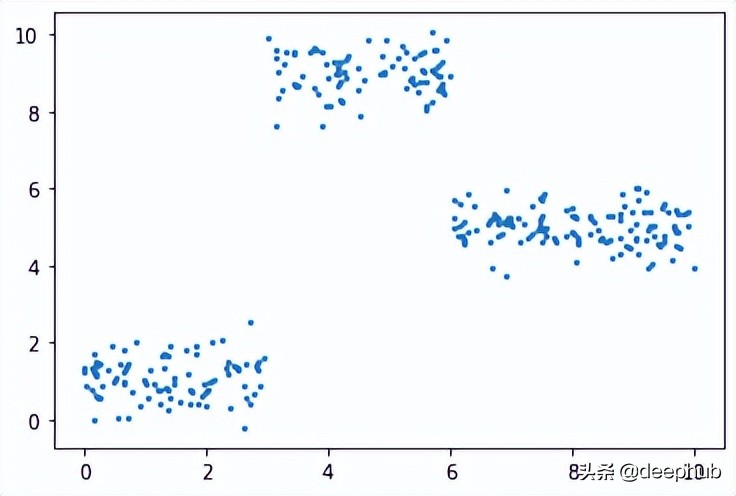
在此數據集上運行了上面的所有相同過程,結果如下

比我們從多項式數據中獲得的誤差低。
最后共享一下上面動圖的代碼:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
#===================================================Create Data
def f(x):
mu, sigma = 0, 1.5
return -x**2 + x + 5 + np.random.normal(mu, sigma, 1)
np.random.seed(1)
x = np.random.uniform(-2, 5, 300)
y = np.array( [f(i) for i in x] )
p = x.argsort()
x = x[p]
y = y[p]
#===================================================Calculate Thresholds
def SSR(r, y): #send numpy array
return np.sum( (r - y)**2 )
SSRs, thresholds = [], []
for i in range(len(x) - 1):
threshold = x[i:i+2].mean()
low = np.take(y, np.where(x < threshold))
high = np.take(y, np.where(x > threshold))
guess_low = low.mean()
guess_high = high.mean()
SSRs.append(SSR(low, guess_low) + SSR(high, guess_high))
thresholds.append(threshold)
#===================================================Animated Plot
fig, (ax1, ax2) = plt.subplots(2,1, sharex = True)
x_data, y_data = [], []
x_data2, y_data2 = [], []
ln, = ax1.plot([], [], 'r--')
ln2, = ax2.plot(thresholds, SSRs, 'ro', markersize = 2)
line = [ln, ln2]
def init():
ax1.scatter(x, y, s = 3)
ax1.title.set_text('Trying Different Thresholds')
ax2.title.set_text('Threshold vs SSR')
ax1.set_ylabel('y values')
ax2.set_xlabel('Threshold')
ax2.set_ylabel('SSR')
return line
def update(frame):
x_data = [x[frame:frame+2].mean()] * 2
y_data = [min(y), max(y)]
line[0].set_data(x_data, y_data)
x_data2.append(thresholds[frame])
y_data2.append(SSRs[frame])
line[1].set_data(x_data2, y_data2)
return line
ani = FuncAnimation(fig, update, frames = 298,
init_func = init, blit = True)
plt.show()