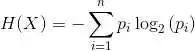決策樹算法是一個強大的預測方法，它非常流行。因為它們的模型能夠讓新手輕而易舉地理解得和專家一樣好，所以它們比較流行。同時，最終生成的決策樹能夠解釋做出特定預測的確切原因，這使它們在實際運用中倍受親睞。

同時，決策樹算法也為更高級的集成模型(如 bagging、隨機森林及 gradient boosting)提供了基礎。

在這篇教程中，你將會從零開始，學習如何用 Python 實現《Classification And Regression Tree algorithm》中所說的內容。

在學完該教程之后，你將會知道：

如何計算并評價數據集中地候選分割點(Candidate Split Point)

如何在決策樹結構中排分配這些分割點

如何在實際問題中應用這些分類和回歸算法

一、概要

本節簡要介紹了關于分類及回歸樹(Classification and Regression Trees)算法的一些內容，并給出了將在本教程中使用的鈔票數據集(Banknote Dataset)。

1.1 分類及回歸樹

分類及回歸樹(CART)是由 Leo Breiman 提出的一個術語，用來描述一種能被用于分類或者回歸預測模型問題的回歸樹算法。

我們將在本教程中主要討論 CART 在分類問題上的應用。

二叉樹(Binary Tree)是 CART 模型的代表之一。這里所說的二叉樹，與數據結構和算法里面所說的二叉樹別無二致，沒有什么特別之處(每個節點可以有 0、1 或 2 個子節點)。

每個節點代表在節點處有一個輸入變量被傳入，并根據某些變量被分類(我們假定該變量是數值型的)。樹的葉節點(又叫做終端節點，Terminal Node)由輸出變量構成，它被用于進行預測。

在樹被創建完成之后，每個新的數據樣本都將按照每個節點的分割條件，沿著該樹從頂部往下，直到輸出一個最終決策。

創建一個二元分類樹實際上是一個分割輸入空間的過程。遞歸二元分類(Recursive Binary Splitting)是一個被用于分割空間的貪心算法。這實際上是一個數值過程：當一系列的輸入值被排列好后，它將嘗試一系列的分割點，測試它們分類完后成本函數(Cost Function)的值。

有最優成本函數(通常是最小的成本函數，因為我們往往希望該值最小)的分割點將會被選擇。根據貪心法(greedy approach)原則，所有的輸入變量和所有可能的分割點都將被測試，并會基于它們成本函數的表現被評估。(譯者注：下面簡述對回歸問題和分類問題常用的成本函數。)

• 回歸問題：對落在分割點確定區域內所有的樣本取誤差平方和(Sum Squared Error)。
• 分類問題：一般采用基尼成本函數(Gini Cost Function)，它能夠表明被分割之后每個節點的純凈度(Node Purity)如何。其中，節點純凈度是一種表明每個節點分類后訓練數據混雜程度的指標。

分割將一直進行，直到每個節點(分類后)都只含有最小數量的訓練樣本或者樹的深度達到了最大值。

1.2 Banknote 數據集

Banknote 數據集，需要我們根據對紙幣照片某些性質的分析，來預測該鈔票的真偽。

該數據集中含有 1372 個樣本，每個樣本由 5 個數值型變量構成。這是一個二元分類問題。如下列舉 5 個變量的含義及數據性質：

1. 圖像經小波變換后的方差(Variance)(連續值)

2. 圖像經小波變換后的偏度(Skewness)(連續值)

3. 圖像經小波變換后的峰度(Kurtosis)(連續值)

4. 圖像的熵(Entropy)(連續值)

5. 鈔票所屬類別(整數，離散值)

如下是數據集前五行數據的樣本。

3.6216,8.6661,-2.8073,-0.44699,0  
4.5459,8.1674,-2.4586,-1.4621,0  
3.866,-2.6383,1.9242,0.10645,0  
3.4566,9.5228,-4.0112,-3.5944,0  
0.32924,-4.4552,4.5718,-0.9888,0  
4.3684,9.6718,-3.9606,-3.1625,0 

使用零規則算法(Zero Rule Algorithm)來預測最常出現類別的情況(譯者注：也就是找到最常出現的一類樣本，然后預測所有的樣本都是這個類別)，對該問的基準準確大概是 50%。

你可以在這里下載并了解更多關于這個數據集的內容：UCI Machine Learning Repository。

請下載該數據集，放到你當前的工作目錄，并重命名該文件為 data_banknote_authentication.csv。

二、教程

本教程分為五大部分：

1. 對基尼系數(Gini Index)的介紹

2.(如何)創建分割點

3.(如何)生成樹模型

4.(如何)利用模型進行預測

5. 對鈔票數據集的案例研究

這些步驟能幫你打好基礎，讓你能夠從零實現 CART 算法，并能將它應用到你子集的預測模型問題中。

2.1 基尼系數

基尼系數是一種評估數據集分割點優劣的成本函數。

數據集的分割點是關于輸入中某個屬性的分割。對數據集中某個樣本而言，分割點會根據某閾值對該樣本對應屬性的值進行分類。他能根據訓練集中出現的模式將數據分為兩類。

基尼系數通過計算分割點創建的兩個類別中數據類別的混雜程度，來表現分割點的好壞。一個完美的分割點對應的基尼系數為 0(譯者注：即在一類中不會出現另一類的數據，每個類都是「純」的)，而最差的分割點的基尼系數則為 1.0(對于二分問題，每一類中出現另一類數據的比例都為 50%，也就是數據完全沒能被根據類別不同區分開)。

下面我們通過一個具體的例子來說明如何計算基尼系數。

我們有兩組數據，每組有兩行。第一組數據中所有行都屬于類別 0(Class 0)，第二組數據中所有的行都屬于類別 1(Class 1)。這是一個完美的分割點。

首先我們要按照下式計算每組數據中各類別數據的比例：

proportion = count(class_value) / count(rows) 

那么，對本例而言，相應的比例為：

group_1_class_0 = 2 / 2 = 1 
group_1_class_1 = 0 / 2 = 0 
group_2_class_0 = 0 / 2 = 0 
group_2_class_1 = 2 / 2 = 1 

基尼系數按照如下公式計算：

gini_index = sum(proportion * (1.0 - proportion)) 

將本例中所有組、所有類數據的比例帶入到上述公式：

gini_index = (group_1_class_0 * (1.0 - group_1_class_0)) + 
(group_1_class_1 * (1.0 - group_1_class_1)) + 
(group_2_class_0 * (1.0 - group_2_class_0)) + 
(group_2_class_1 * (1.0 - group_2_class_1)) 

化簡，得：

gini_index = 0 + 0 + 0 + 0 = 0 

如下是一個叫做 gini_index() 的函數，它能夠計算給定數據的基尼系數(組、類別都以列表(list)的形式給出)。其中有些算法魯棒性檢測，能夠避免對空組除以 0 的情況。

# Calculate the Gini index for a split dataset 
def gini_index(groups, class_values): 
gini = 0.0 
for class_value in class_values: 
for group in groups: 
size = len(group) 
if size == 0: 
continue 
proportion = [row[-1] for row in group].count(class_value) / float(size) 
gini += (proportion * (1.0 - proportion)) 
return gini 

我們可以根據上例來測試該函數的運行情況，也可以測試最差分割點的情況。完整的代碼如下：

# Calculate the Gini index for a split dataset 
def gini_index(groups, class_values): 
gini = 0.0 
for class_value in class_values: 
for group in groups: 
size = len(group) 
if size == 0: 
continue 
proportion = [row[-1] for row in group].count(class_value) / float(size) 
gini += (proportion * (1.0 - proportion)) 
return gini 
# test Gini values 
print(gini_index([[[1, 1], [1, 0]], [[1, 1], [1, 0]]], [0, 1])) 
print(gini_index([[[1, 0], [1, 0]], [[1, 1], [1, 1]]], [0, 1])) 

運行該代碼，將會打印兩個基尼系數，其中第一個對應的是最差的情況為 1.0，第二個對應的是最好的情況為 0.0。

1.0 
0.0 

2.2 創建分割點

一個分割點由數據集中的一個屬性和一個閾值構成。

我們可以將其總結為對給定的屬性確定一個分割數據的閾值。這是一種行之有效的分類數據的方法。

創建分割點包括三個步驟，其中第一步已在計算基尼系數的部分討論過。余下兩部分分別為：

1. 分割數據集。

2. 評價所有(可行的)分割點。

我們具體看一下每個步驟。

2.2.1 分割數據集

分割數據集意味著我們給定數據集某屬性(或其位于屬性列表中的下表)及相應閾值的情況下，將數據集分為兩個部分。

一旦數據被分為兩部分，我們就可以使用基尼系數來評估該分割的成本函數。

分割數據集需要對每行數據進行迭代，根據每個數據點相應屬性的值與閾值的大小情況將該數據點放到相應的部分(對應樹結構中的左叉與右叉)。

如下是一個名為 test_split() 的函數，它能實現上述功能：

# Split a dataset based on an attribute and an attribute value 
def test_split(index, value, dataset): 
 left, right = list(), list() 
 for row in dataset: 
 if row[index] < value: 
 left.append(row) 
 else: 
 right.append(row) 
 return left, right 

代碼還是很簡單的。

注意，在代碼中，屬性值大于或等于閾值的數據點被分類到了右組中。

2.2.2 評價所有分割點

在基尼函數 gini_index() 和分類函數 test_split() 的幫助下，我們可以開始進行評估分割點的流程。

對給定的數據集，對每一個屬性，我們都要檢查所有的可能的閾值使之作為候選分割點。然后，我們將根據這些分割點的成本(cost)對其進行評估，最終挑選出最優的分割點。

當最優分割點被找到之后，我們就能用它作為我們決策樹中的一個節點。

而這也就是所謂的窮舉型貪心算法。

在該例中，我們將使用一個詞典來代表決策樹中的一個節點，它能夠按照變量名儲存數據。當選擇了最優分割點并使用它作為樹的新節點時，我們存下對應屬性的下標、對應分割值及根據分割值分割后的兩部分數據。

分割后地每一組數據都是一個更小規模地數據集(可以繼續進行分割操作)，它實際上就是原始數據集中地數據按照分割點被分到了左叉或右叉的數據集。你可以想象我們可以進一步將每一組數據再分割，不斷循環直到建構出整個決策樹。

如下是一個名為 get_split() 的函數，它能實現上述的步驟。你會發現，它遍歷了每一個屬性(除了類別值)以及屬性對應的每一個值，在每次迭代中它都會分割數據并評估該分割點。

當所有的檢查完成后，最優的分割點將被記錄并返回。

# Select the best split point for a dataset 
def get_split(dataset): 
 class_values = list(set(row[-1] for row in dataset)) 
 b_index, b_value, b_score, b_groups = 999, 999, 999, None 
 for index in range(len(dataset[0])-1): 
 for row in dataset: 
 groups = test_split(index, row[index], dataset) 
 gini = gini_index(groups, class_values) 
 if gini < b_score: 
 b_index, b_value, b_score, b_groups = index, row[index], gini, groups 
 return {'index':b_index, 'value':b_value, 'groups':b_groups} 

我們能在一個小型合成的數據集上來測試這個函數以及整個數據集分割的過程。

X1 X2 Y 
2.771244718 1.784783929 0 
1.728571309 1.169761413 0 
3.678319846 2.81281357 0 
3.961043357 2.61995032 0 
2.999208922 2.209014212 0 
7.497545867 3.162953546 1 
9.00220326 3.339047188 1 
7.444542326 0.476683375 1 
10.12493903 3.234550982 1 
6.642287351 3.319983761 1 

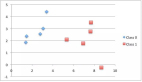
同時，我們可以使用不同顏色標記不同的類，將該數據集繪制出來。由圖可知，我們可以從 X1 軸(即圖中的 X 軸)上挑出一個值來分割該數據集。

 

范例所有的代碼整合如下：

# Split a dataset based on an attribute and an attribute value 
def test_split(index, value, dataset): 
 left, right = list(), list() 
 for row in dataset: 
 if row[index] < value: 
 left.append(row) 
 else: 
 right.append(row) 
 return left, right 
  
# Calculate the Gini index for a split dataset 
def gini_index(groups, class_values): 
 gini = 0.0 
 for class_value in class_values: 
 for group in groups: 
 size = len(group) 
 if size == 0: 
 continue 
 proportion = [row[-1] for row in group].count(class_value) / float(size) 
 gini += (proportion * (1.0 - proportion)) 
 return gini 
  
# Select the best split point for a dataset 
def get_split(dataset): 
 class_values = list(set(row[-1] for row in dataset)) 
 b_index, b_value, b_score, b_groups = 999, 999, 999, None 
 for index in range(len(dataset[0])-1): 
 for row in dataset: 
 groups = test_split(index, row[index], dataset) 
 gini = gini_index(groups, class_values) 
 print('X%d < %.3f Gini=%.3f' % ((index+1), row[index], gini)) 
 if gini < b_score: 
 b_index, b_value, b_score, b_groups = index, row[index], gini, groups 
 return {'index':b_index, 'value':b_value, 'groups':b_groups} 
  
dataset = [[2.771244718,1.784783929,0], 
 [1.728571309,1.169761413,0], 
 [3.678319846,2.81281357,0], 
 [3.961043357,2.61995032,0], 
 [2.999208922,2.209014212,0], 
 [7.497545867,3.162953546,1], 
 [9.00220326,3.339047188,1], 
 [7.444542326,0.476683375,1], 
 [10.12493903,3.234550982,1], 
 [6.642287351,3.319983761,1]] 
split = get_split(dataset) 
print('Split: [X%d < %.3f]' % ((split['index']+1), split['value'])) 

優化后的 get_split() 函數能夠輸出每個分割點及其對應的基尼系數。

運行如上的代碼后，它將 print 所有的基尼系數及其選中的最優分割點。在此范例中，它選中了 X1<6.642 作為最終完美分割點(它對應的基尼系數為 0)。

X1 < 2.771 Gini=0.494 
X1 < 1.729 Gini=0.500 
X1 < 3.678 Gini=0.408 
X1 < 3.961 Gini=0.278 
X1 < 2.999 Gini=0.469 
X1 < 7.498 Gini=0.408 
X1 < 9.002 Gini=0.469 
X1 < 7.445 Gini=0.278 
X1 < 10.125 Gini=0.494 
X1 < 6.642 Gini=0.000 
X2 < 1.785 Gini=1.000 
X2 < 1.170 Gini=0.494 
X2 < 2.813 Gini=0.640 
X2 < 2.620 Gini=0.819 
X2 < 2.209 Gini=0.934 
X2 < 3.163 Gini=0.278 
X2 < 3.339 Gini=0.494 
X2 < 0.477 Gini=0.500 
X2 < 3.235 Gini=0.408 
X2 < 3.320 Gini=0.469 
Split: [X1 < 6.642] 

既然我們現在已經能夠找出數據集中最優的分割點，那我們現在就來看看我們能如何應用它來建立一個決策樹。

2.3 生成樹模型

創建樹的根節點(root node)是比較方便的，可以調用 get_split() 函數并傳入整個數據集即可達到此目的。但向樹中增加更多的節點則比較有趣。

建立樹結構主要分為三個步驟：

1. 創建終端節點

2. 遞歸地分割

3. 建構整棵樹

2.3.1 創建終端節點

我們需要決定何時停止樹的「增長」。

我們可以用兩個條件進行控制：樹的深度和每個節點分割后的數據點個數。

最大樹深度：這代表了樹中從根結點算起節點數目的上限。一旦樹中的節點樹達到了這一上界，則算法將會停止分割數據、增加新的節點。更神的樹會更為復雜，也更有可能過擬合訓練集。

最小節點記錄數：這是某節點分割數據后分個部分數據個數的最小值。一旦達到或低于該最小值，則算法將會停止分割數據、增加新的節點。將數據集分為只有很少數據點的兩個部分的分割節點被認為太具針對性，并很有可能過擬合訓練集。

這兩個方法基于用戶給定的參數，參與到樹模型的構建過程中。

此外，還有一個情況。算法有可能選擇一個分割點，分割數據后所有的數據都被分割到同一組內(也就是左叉、右叉只有一個分支上有數據，另一個分支沒有)。在這樣的情況下，因為在樹的另一個分叉沒有數據，我們不能繼續我們的分割與添加節點的工作。

基于上述內容，我們已經有一些停止樹「增長」的判別機制。當樹在某一結點停止增長的時候，該節點被稱為終端節點，并被用來進行最終預測。

預測的過程是通過選擇組表征值進行的。當遍歷樹進入到最終節點分割后的數據組中，算法將會選擇該組中最普遍出現的值作為預測值。

如下是一個名為 to_terminal() 的函數，對每一組收據它都能選擇一個表征值。他能夠返回一系列數據點中最普遍出現的值。

# Create a terminal node value 
def to_terminal(group): 
outcomes = [row[-1] for row in group] 
return max(set(outcomes), key=outcomes.count) 

2.3.2 遞歸分割

在了解了如何及何時創建終端節點后，我們現在可以開始建立樹模型了。

建立樹地模型，需要我們對給定的數據集反復調用如上定義的 get_split() 函數，不斷創建樹中的節點。

在已有節點下加入的新節點叫做子節點。對樹中的任意節點而言，它可能沒有子節點(則該節點為終端節點)、一個子節點(則該節點能夠直接進行預測)或兩個子節點。在程序中，在表示某節點的字典中，我們將一棵樹的兩子節點命名為 left 和 right。

一旦一個節點被創建，我們就可以遞歸地對在該節點被分割得到的兩個子數據集上調用相同的函數，來分割子數據集并創建新的節點。

如下是一個實現該遞歸過程的函數。它的輸入參數包括：某一節點(node)、最大樹深度(max_depth)、最小節點記錄數(min_size)及當前樹深度(depth)。

顯然，一開始運行該函數時，根節點將被傳入，當前深度為 1。函數的功能分為如下幾步：

1. 首先，該節點分割的兩部分數據將被提取出來以便使用，同時數據將被在節點中刪除(隨著分割工作的逐步進行，之前的節點不需要再使用相應的數據)。

2. 然后，我們將會檢查該節點的左叉及右叉的數據集是否為空。如果是，則其將會創建一個終端節點。

3. 同時，我們會檢查是否到達了最大深度。如果是，則其將會創建一個終端節點。

4. 接著，我們將對左子節點進一步操作。若該組數據個數小于閾值，則會創建一個終端節點并停止進一步操作。否則它將會以一種深度優先的方式創建并添加節點，直到該分叉達到底部。

5. 對右子節點同樣進行上述操作，不斷增加節點直到達到終端節點。

2.3.3 建構整棵樹

我們將所有的內容整合到一起。

創建一棵樹包括創建根節點及遞歸地調用 split() 函數來不斷地分割數據以構建整棵樹。

如下是實現上述功能的 bulid_tree() 函數的簡化版本。

# Build a decision tree 
def build_tree(train, max_depth, min_size): 
root = get_split(dataset) 
split(root, max_depth, min_size, 1) 
return root 

我們可以在如上所述的合成數據集上測試整個過程。如下是完整的案例。

在其中還包括了一個 print_tree() 函數，它能夠遞歸地一行一個地打印出決策樹的節點。經過它打印的不是一個明顯的樹結構，但它能給我們關于樹結構的大致印象，并能幫助決策。

# Split a dataset based on an attribute and an attribute value 
def test_split(index, value, dataset): 
left, right = list(), list() 
for row in dataset: 
if row[index] < value: 
left.append(row) 
else: 
right.append(row) 
return left, right 
 
# Calculate the Gini index for a split dataset 
def gini_index(groups, class_values): 
gini = 0.0 
for class_value in class_values: 
for group in groups: 
size = len(group) 
if size == 0: 
continue 
proportion = [row[-1] for row in group].count(class_value) / float(size) 
gini += (proportion * (1.0 - proportion)) 
return gini 
 
# Select the best split point for a dataset 
def get_split(dataset): 
class_values = list(set(row[-1] for row in dataset)) 
b_index, b_value, b_score, b_groups = 999, 999, 999, None 
for index in range(len(dataset[0])-1): 
for row in dataset: 
groups = test_split(index, row[index], dataset) 
gini = gini_index(groups, class_values) 
if gini < b_score: 
b_index, b_value, b_score, b_groups = index, row[index], gini, groups 
return {'index':b_index, 'value':b_value, 'groups':b_groups} 
 
# Create a terminal node value 
def to_terminal(group): 
outcomes = [row[-1] for row in group] 
return max(set(outcomes), key=outcomes.count) 
 
# Create child splits for a node or make terminal 
def split(node, max_depth, min_size, depth): 
left, right = node['groups'] 
del(node['groups']) 
# check for a no split 
if not left or not right: 
node['left'] = node['right'] = to_terminal(left + right) 
return 
# check for max depth 
if depth >= max_depth: 
node['left'], node['right'] = to_terminal(left), to_terminal(right) 
return 
# process left child 
if len(left) <= min_size: 
node['left'] = to_terminal(left) 
else: 
node['left'] = get_split(left) 
split(node['left'], max_depth, min_size, depth+1) 
# process right child 
if len(right) <= min_size: 
node['right'] = to_terminal(right) 
else: 
node['right'] = get_split(right) 
split(node['right'], max_depth, min_size, depth+1) 
 
# Build a decision tree 
def build_tree(train, max_depth, min_size): 
root = get_split(dataset) 
split(root, max_depth, min_size, 1) 
return root 
 
# Print a decision tree 
def print_tree(node, depth=0): 
if isinstance(node, dict): 
print('%s[X%d < %.3f]' % ((depth*' ', (node['index']+1), node['value']))) 
print_tree(node['left'], depth+1) 
print_tree(node['right'], depth+1) 
else: 
print('%s[%s]' % ((depth*' ', node))) 
 
dataset = [[2.771244718,1.784783929,0], 
[1.728571309,1.169761413,0], 
[3.678319846,2.81281357,0], 
[3.961043357,2.61995032,0], 
[2.999208922,2.209014212,0], 
[7.497545867,3.162953546,1], 
[9.00220326,3.339047188,1], 
[7.444542326,0.476683375,1], 
[10.12493903,3.234550982,1], 
[6.642287351,3.319983761,1]] 
tree = build_tree(dataset, 1, 1) 
print_tree(tree) 

在運行過程中，我們能修改樹的最大深度，并在打印的樹上觀察其影響。

當最大深度為 1 時(即調用 build_tree() 函數時第二個參數)，我們可以發現該樹使用了我們之前發現的完美分割點(作為樹的唯一分割點)。該樹只有一個節點，也被稱為決策樹樁。

[X1 < 6.642]  
[0]  
[1] 

當最大深度加到 2 時，我們迫使輸算法不需要分割的情況下強行分割。結果是，X1 屬性在左右叉上被使用了兩次來分割這個本已經完美分割的數據。

[X1 < 6.642] 
[X1 < 2.771] 
[0] 
[0] 
[X1 < 7.498] 
[1] 
[1] 

最后，我們可以試試最大深度為 3 的情況：

[X1 < 6.642] 
[X1 < 2.771] 
[0] 
[X1 < 2.771] 
[0] 
[0] 
[X1 < 7.498] 
[X1 < 7.445] 
[1] 
[1] 
[X1 < 7.498] 
[1] 
[1] 

這些測試表明，我們可以優化代碼來避免不必要的分割。請參見延伸章節的相關內容。

現在我們已經可以(完整地)創建一棵決策樹了，那么我們來看看如何用它來在新數據上做出預測吧。

2.4 利用模型進行預測

使用決策樹模型進行決策，需要我們根據給出的數據遍歷整棵決策樹。

與前面相同，我們仍需要使用一個遞歸函數來實現該過程。其中，基于某分割點對給出數據的影響，相同的預測規則被應用到左子節點或右子節點上。

我們需要檢查對某子節點而言，它是否是一個可以被作為預測結果返回的終端節點，又或是他是否含有下一層的分割節點需要被考慮。

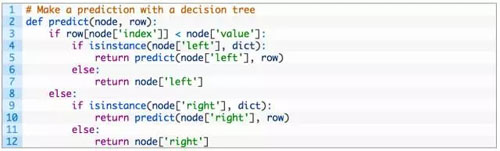
如下是實現上述過程的名為 predict() 函數，你可以看到它是如何處理給定節點的下標與數值的。

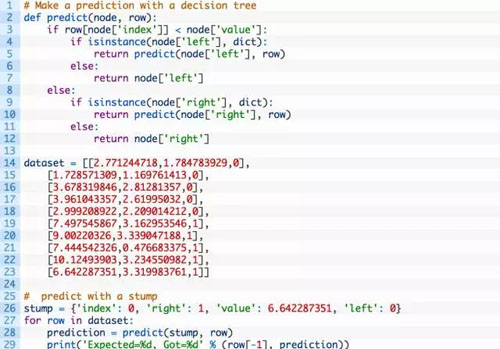
接著，我們使用合成的數據集來測試該函數。如下是一個使用僅有一個節點的硬編碼樹(即決策樹樁)的案例。該案例中對數據集中的每個數據進行了預測。

運行該例子，它將按照預期打印出每個數據的預測結果。

Expected=0, Got=0 
Expected=0, Got=0 
Expected=0, Got=0 
Expected=0, Got=0 
Expected=0, Got=0 
Expected=1, Got=1 
Expected=1, Got=1 
Expected=1, Got=1 
Expected=1, Got=1 
Expected=1, Got=1 

現在，我們不僅掌握了如何創建一棵決策樹，同時還知道如何用它進行預測。那么，我們就來試試在實際數據集上來應用該算法吧。

2.5 對鈔票數據集的案例研究

該節描述了在鈔票數據集上使用了 CART 算法的流程。

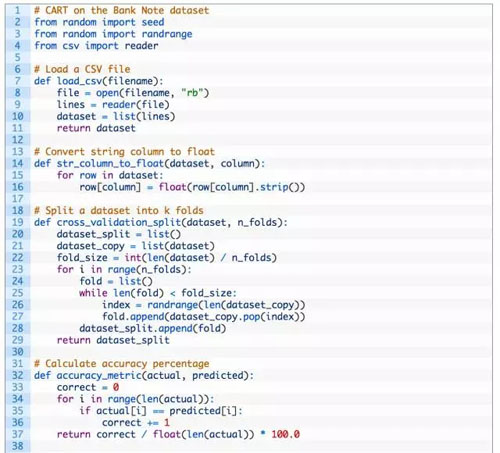
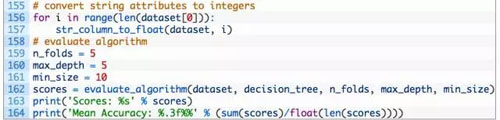
第一步是導入數據，并轉換載入的數據到數值形式，使得我們能夠用它來計算分割點。對此，我們使用了輔助函數 load_csv() 載入數據及 str_column_to_float() 以轉換字符串數據到浮點數。

我們將會使用 5 折交叉驗證法(5-fold cross validation)來評估該算法的表現。這也就意味著，對一個記錄，將會有 1273/5=274.4 即 270 個數據點。我們將會使用輔助函數 evaluate_algorithm() 來評估算法在交叉驗證集上的表現，用 accuracy_metric() 來計算預測的準確率。

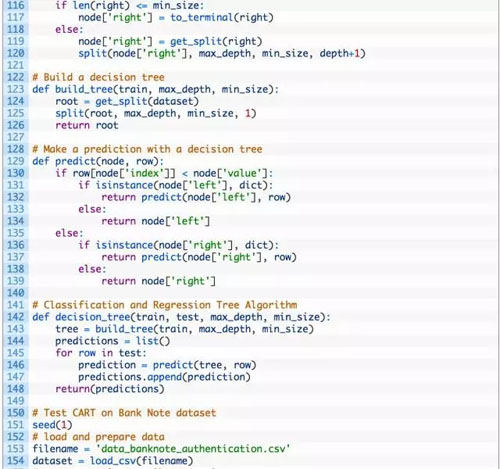
完成的代碼如下：

上述使用的參數包括：max_depth 為 5，min_size 為 10。經過了一些實現后，我們確定了上述 CART 算法的使用的參數，但這不代表所使用的參數就是最優的。

運行該案例，它將會 print 出對每一部分數據的平均分類準確度及對所有部分數據的平均表現。

從數據中你可以發現，CART 算法選擇的分類設置，達到了大約 83% 的平均分類準確率。其表現遠遠好于只有約 50% 正確率的零規則算法(Zero Rule algorithm)。

Scores: [83.57664233576642, 84.30656934306569, 85.76642335766424, 81.38686131386861, 81.75182481751825]

Mean Accuracy: 83.358%

三、延伸

本節列出了關于該節的延伸項目，你可以根據此進行探索。

1. 算法調參(Algorithm Tuning)：在鈔票數據集上使用的 CART 算法未被調參。你可以嘗試不同的參數數值以獲取更好的更優的結果。

2. 交叉熵(Cross Entropy)：另一個用來評估分割點的成本函數是交叉熵函數(對數損失)。你能夠嘗試使用該成本函數作為替代。

3. 剪枝(Tree Pruning)：另一個減少在訓練過程中過擬合程度的重要方法是剪枝。你可以研究并嘗試實現一些剪枝的方法。

4. 分類數據集(Categorical Dataset)：在上述例子中，其樹模型被設計用于解決數值型或有序數據。你可以嘗試修改樹模型(主要修改分割的屬性，用等式而非排序的形式)，使之能夠應對分類型的數據。

5. 回歸問題(Regression)：可以通過使用不同的成本函數及不同的創建終端節點的方法，來讓該模型能夠解決一個回歸問題。

6. 更多數據集：你可以嘗試將該算法用于 UCI Machine Learning Repository 上其他的數據集。

【本文是51CTO專欄機構機器之心的原創文章，微信公眾號“機器之心( id: almosthuman2014)”】

戳這里，看該作者更多好文