大家好，我是年年！今天的內容是關于一道算法題——青蛙跳臺階。這是一個面試很喜歡考的題，看到它，大部分人腦海中應該立馬出現：斐波那契亞數列——遞歸——f(n)=f(n-1)+f(n-2)。

但輔導的小伙伴上周在面試中遇到的問題是：除了遞歸，能不能寫出別的解法，降低算法的時間復雜度。這篇文章給出這道題的更優解。

題目

一只青蛙一次可以跳上1級臺階，也可以跳上2級臺階。求該青蛙跳上一個n級的臺階總共有多少種跳法？

分析

這是一個最基礎的動態規劃類問題，首先來講一下思路：當n較小時，可以直接枚舉得到結果：

1. n=1時，青蛙僅有直接跳上一級臺階這種跳法，即一種跳法;
2. n=2時，青蛙可以先跳 上 1 級，然后再跳 上 1 級到達2級臺階，；也可以直接跳 2 級臺階，即一共有兩種解法;

當n較大時，去枚舉不現實了。但可以想象一下青蛙“最后一跳”有哪些情況：因為青蛙一次可以跳1個或2個臺階，所以只可能是兩種情況：從n-1級跳1級上去，以及從n-2階的位置跳2級上去。我們想要知道跳n級臺階有多少種解法，只需要知道跳n-1級臺階和跳n-2級臺階的跳法，把他們加起來就可以。即得到一個公式f(n)=f(n-1)+f(n-2)。

常規解法(遞歸)

看到這個式子f(n)=f(n-1)+f(n-2)，應該很快能反應：斐波那契亞數列，代碼很容易寫出來。遞歸的關鍵是確認遞歸出口，即：當只有1級臺階，只有一種跳法；只有2級臺階時，有兩種跳法。

代碼如下：

function frogJump(n) {
  if (n >= 3) {
    let result = frogJump(n - 1) + frogJump(n - 2)
    return result
  } else if (n === 1) {
    return 1
  }else if(n===2) {
    return 2
  }
}
let result = frogJump(6) // 13
console.log(result)

復雜度分析

上面這張遞歸解法只有60分，因為時間復雜度太高。

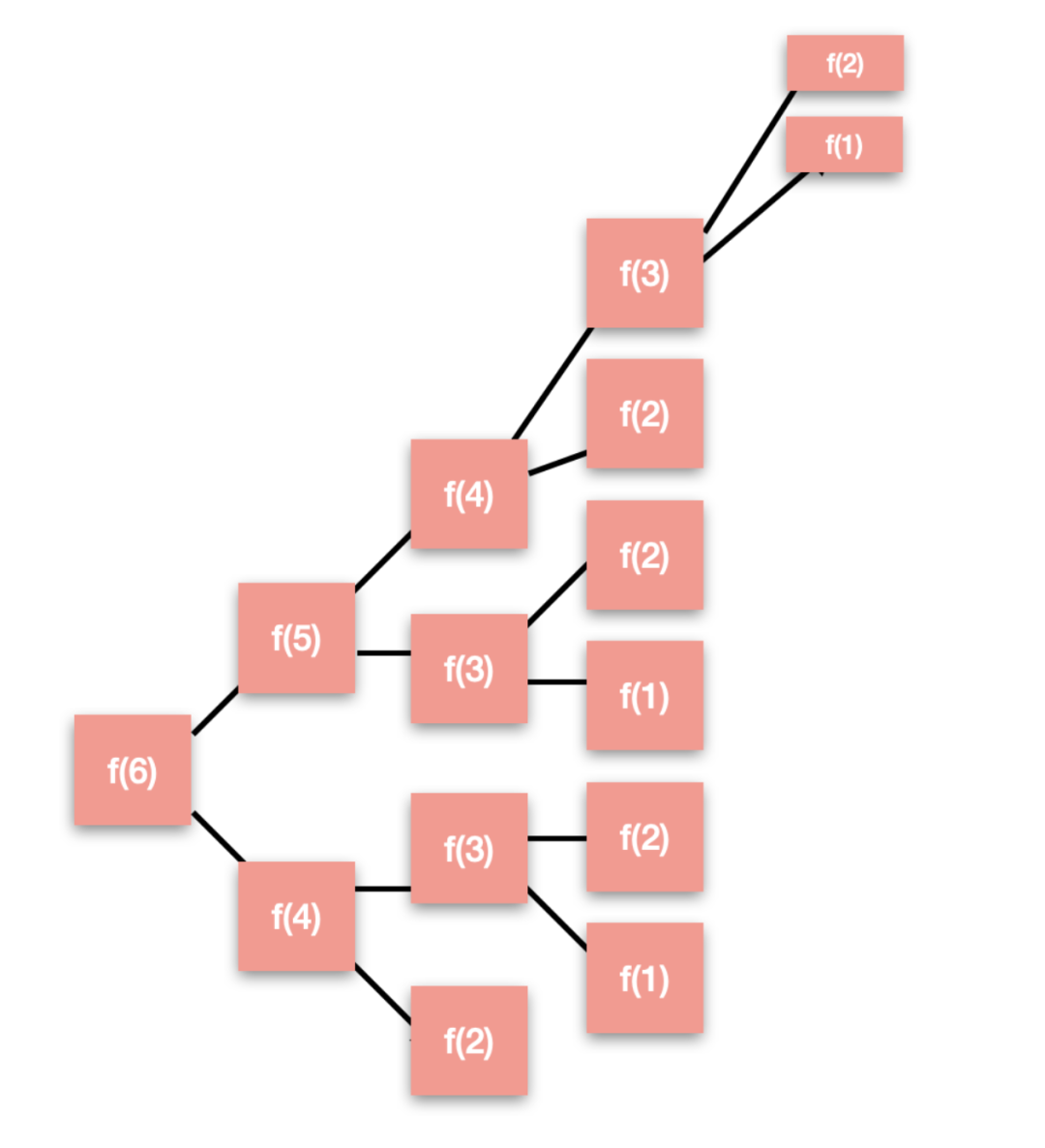
可以看到，因為沒有把結果保存，出現了很多重復計算的步驟：為了得到f(6)的結果，需要計算f(5)和f(4),為了得到f(5)的結果，需要計算f(4)和f(3)，這里兩次計算f(4)是獨立的事件，也就是說，我們做了很多重復工作。

把上面這棵樹補充成一個完全樹，如下：

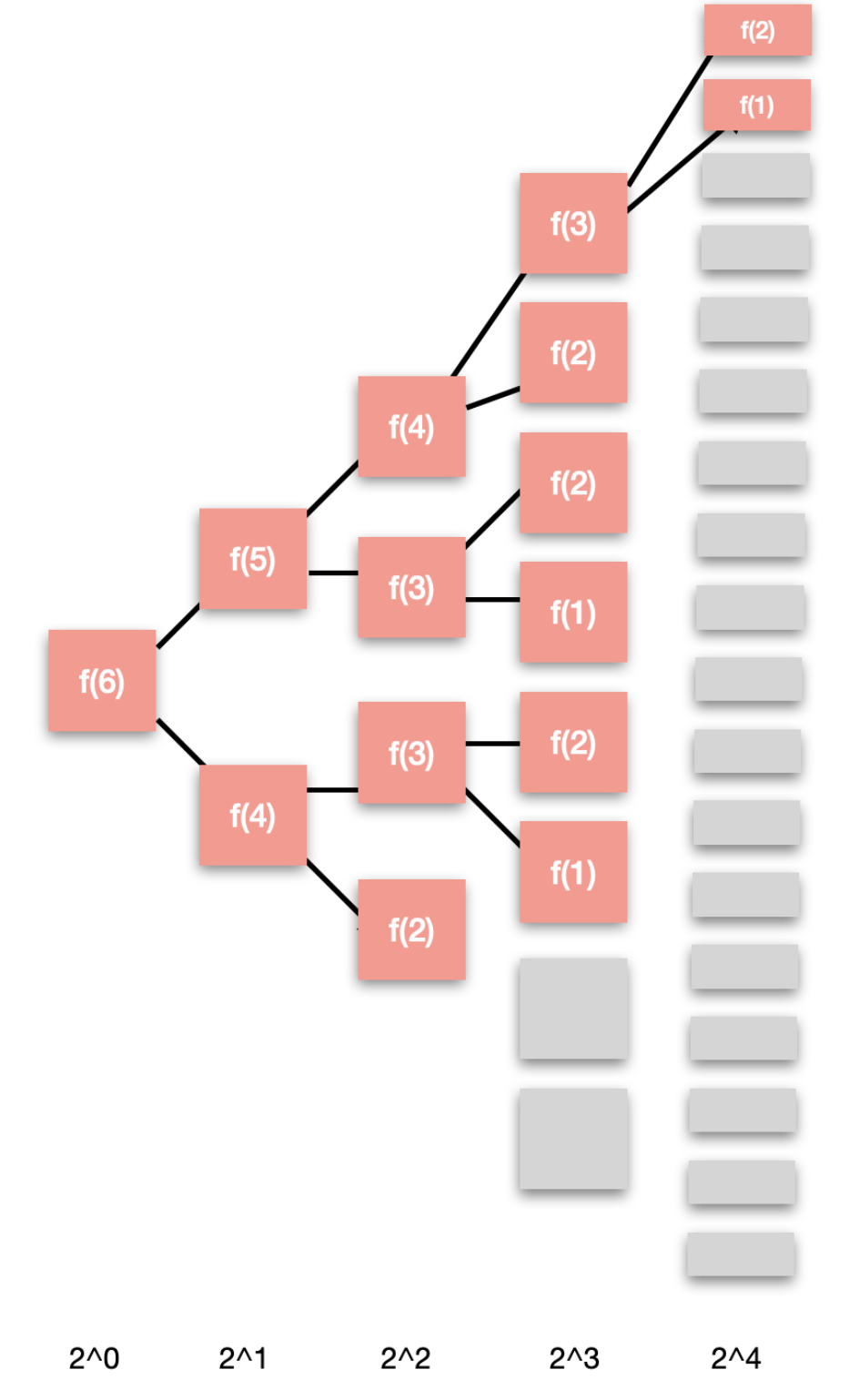
這種算法復雜度可以用2^0+2^1+2^2+...+2^4表示，即時間復雜度近似為O(2^N)(回憶一下高中數學的等比數列)。

而空間復雜度是調用棧的深度，從上面的圖可以看出來，最大的棧深是n-1，即空間復雜度是O(n)

進階解法（尾遞歸）

上面這種解法時間復雜度很高在于做了很多重復計算，從遞歸公式能看出來：f(n)=f(n-1)+f(n-2)=f(n-2)+f(n-3)+f(n-3)+f(n-4)，一生二，二生四，四生八，整個計算過程就像是發散開來一樣。每一次調用都沒有保留下“狀態”，造成了大量的計算浪費。

只要我們保留下計算的結果，就可以把時間復雜度控制在O(n)，也就是下面“尾遞歸”。

代碼如下：

function frogJump(first, second, n) {
  let a = first,
  b = second
  let c = first + second
  if (n > 3) {
    a = second
    b = first + second
    return frogJump(a, b, n - 1)
  } else if (n === 3) {
    return c
  } else if ( n === 2) {
    return 2
  } else if(n===1) {
    return 1
  }
}
let result = frogJump(1, 2, 6)
console.log(result)

我們用abc三個變量，把計算的結果保存下來，避免重復的工作。從first=1,second=2開始計算，每次遞歸調用更新first和second的值，這就是在保存下每次計算的結果，供下一次遞歸使用。直到n=3，滿足遞歸終止條件。

復雜度分析

這種尾遞歸，時間復雜度只有O(N)，但他是幾種解法里面最難想到，也最難理解的。空間復雜度即遞歸的深度，是O(N)。

進階解法（循環）

循環和遞歸是可以相互轉化的，所以一種優化思路是用循環把上面的邏輯實現。

function frogJump(n) {
  if (n === 1) {
    return 1
  } else if(n===2) {
    return 2
  }else {
    let a = 1,
      b = 2,
      c
    let count = 0
    while (count < n - 2) {
      c = a + b
      a = b
      b = c
      count++
    }
    return c
  }
}
let result = frogJump(6)
console.log(result)

我們首先知道了計算公式f(n)=f(n-1)+f(n-2);并且知道：當只有一級臺階時，只有一種解法，只有兩級臺階時，只有兩種解法。如果有三級臺階，計算一次即可（計算F(3)）；有四級臺階，計算兩次即可（計算f(3)、f(4)）所以可推，當計算f（n）時，需要計算的次數是n-2，這就是循環的次數。上面的代碼便不難寫出。

復雜度分析

通過循環，我們同樣保留下了計算的結果，減少了重復的工作，時間復雜度是O(N)。空間復雜度是O(1)。

結語

通過這道算法題，能感受到循環通常比遞歸在時間復雜度上有優勢，但它更難想到，代碼塊也會更復雜。通常一個算法的遞歸和循環是可以相互轉化的，可以試著把之前刷過的題用不同的思路實現一下。