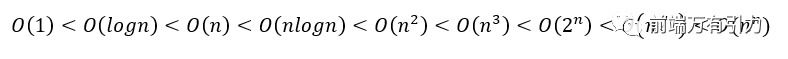[[407579]]

寫在前面

大廠秋招提前批已經(jīng)開啟，吹響了應(yīng)屆生秋招的號(hào)角，也就意味著大家要加入殘酷的招聘競爭。筆試面試是規(guī)范求職過去的坎，而算法對于大多數(shù)人而言是是道難關(guān)，只有通過系統(tǒng)學(xué)習(xí)和理解刷題才能征服它。

為了幫助更多人去理解數(shù)據(jù)結(jié)構(gòu)和算法，將開辟新的博文系列《懂點(diǎn)算法》，希望大家能夠渡過痛苦的日子。本人在算法研究上，能力有限，希望大家能夠取其精華，汲取干貨。

什么是算法

算法(Algorithm)是指用來操作數(shù)據(jù)、解決程序問題的一組方法。

衡量不同算法之間的優(yōu)劣有兩種方法：

• 事后統(tǒng)計(jì)法：通過統(tǒng)計(jì)、監(jiān)控，利用計(jì)算機(jī)計(jì)時(shí)器對不同算法的運(yùn)行時(shí)間進(jìn)行比較，從而確定算法效率的高低，但是具有非常大的局限性。
• 事前分析估算法：在計(jì)算機(jī)程序編制前，依據(jù)統(tǒng)計(jì)方法對算法進(jìn)行估算。

舉個(gè)栗子，我們知道斐波那契數(shù)列的規(guī)律是：數(shù)列從第3項(xiàng)開始，每一項(xiàng)數(shù)值是前兩項(xiàng)數(shù)值之和。即：0,1,1,2,3,5,8...

分析：我們觀察斐波那契數(shù)列的規(guī)律，可以看到數(shù)列在使用算法進(jìn)行表示的時(shí)候，需要分為兩種情況，即前兩項(xiàng)，和第三項(xiàng)開始后的元素的計(jì)算。

最簡單的方法是使用遞歸進(jìn)行實(shí)現(xiàn)斐波那契數(shù)列的算法：

function fib(num){ 
  if(num <= 1) return num; 
  return fib(num - 1) + fib(num - 2); 
} 

當(dāng)然，也可以使用循環(huán)方法進(jìn)行實(shí)現(xiàn)：

function fib(num){ 
  if(num <= 1) return num; 
  let num1 = 0, num2 = 1; 
  for(let i = 0; i < num - 1; i++){ 
    // 每次加都是前兩項(xiàng)之和 
    let sum = num1 + num2; 
    // 相加之前num2要作為下一次相加的num1 
    num1 = num2; 
    // 相加的結(jié)果要作為下一個(gè)num2 
    num2 = sum; 
    // 但是呢，上面兩句代碼不可交換哦 
  } 
  return num2; 
} 

其實(shí)，高級(jí)程序語言編寫的程序在計(jì)算機(jī)上運(yùn)行的消耗時(shí)間取決于以下因素：

• 算法采用的策略、方法(算法的好壞)
• 編譯產(chǎn)生的代碼質(zhì)量(軟件性能)
• 問題的輸入規(guī)模(輸入量的多少)
• 機(jī)器執(zhí)行指令的速度(硬件性能)

總的來說，程序的運(yùn)行時(shí)間主要取決于算法的好壞和問題的輸入規(guī)模。

時(shí)間復(fù)雜度和空間復(fù)雜度

我們都學(xué)過高斯的故事，主要內(nèi)容是這樣的：在高斯上學(xué)時(shí)老師提問如何計(jì)算100以內(nèi)非0自然數(shù)的和，即計(jì)算1+2+……+99+100=? 當(dāng)時(shí)很多同學(xué)都在從頭加到尾計(jì)算，但是高斯并沒有忙著去計(jì)算，而是思考問題。

經(jīng)過高斯觀察后發(fā)現(xiàn)，第一項(xiàng)與最后一項(xiàng)的和等于第二項(xiàng)與倒數(shù)第二項(xiàng)的和一樣，都是101，同時(shí)他發(fā)現(xiàn)其他項(xiàng)也符合這樣的規(guī)律。而總共有50對，所以結(jié)果就是101×50=5050。于是，他成為班里第一個(gè)計(jì)算出答案的人。

告訴我們道理：磨刀不誤砍柴工，用對方法更輕松。

那么，我們仔細(xì)分析下高斯算法和常規(guī)算法的優(yōu)劣。

常規(guī)算法：

function commonFunc(){ 
  let sum = 0; //執(zhí)行一次 
  for(let i = 1; i <= 100; i++){ //執(zhí)行n+1次 
    sum += i;//執(zhí)行n次 
  } 
  return sum;//執(zhí)行1次 
} 

高斯算法：

function guassFunc(){ 
  let sum = 0;//執(zhí)行1次 
  sum = (1 * ｎ) ＊ ｎ／２；//執(zhí)行1次 
  return sum;//執(zhí)行1次 
} 

如上所示，常規(guī)算法的執(zhí)行次數(shù)是2n+3次，而高斯算法的執(zhí)行次數(shù)是3次。由于首尾語句的執(zhí)行次數(shù)是相同，主要關(guān)注中間算法部分則是n次與1次的區(qū)別，很顯然高斯算法遠(yuǎn)優(yōu)于常規(guī)算法。

算法時(shí)間復(fù)雜度

我們看下《大話數(shù)據(jù)結(jié)構(gòu)》中是如何定義算法時(shí)間復(fù)雜度的。

算法時(shí)間復(fù)雜度：在進(jìn)行算法分析時(shí)，語句總的執(zhí)行次數(shù)T(n)是關(guān)于問題規(guī)模n的函數(shù)，進(jìn)而分析得到T(n)隨n的變化情況并確定T(n)的數(shù)量級(jí)。算法的時(shí)間復(fù)雜度，就是算法的時(shí)間量度，記作：T(n)=O(f(n))。它表示隨時(shí)間規(guī)模n的增大，算法執(zhí)行時(shí)間的增長率和f(n)的增長率相同，稱作算法的漸進(jìn)時(shí)間復(fù)雜度，簡稱時(shí)間復(fù)雜度。

我給你翻譯翻譯，就是說時(shí)間復(fù)雜度是用于估算程序運(yùn)行時(shí)間的量度。假設(shè)算法的問題規(guī)模為n，那么操作單元數(shù)量(用于表示程序消耗的時(shí)間)，隨著數(shù)據(jù)規(guī)模n的增大，算法執(zhí)行時(shí)間的增長率和f(n)的增長率相同，稱作時(shí)間復(fù)雜度O(f(n))。

T(n)=O(f(n))

• T(n)表示代碼執(zhí)行的時(shí)間
• n表示數(shù)據(jù)規(guī)模的大小
• f(n)表示每行代碼執(zhí)行的次數(shù)總和
• O表示代碼執(zhí)行時(shí)間T(n)與T(n)成正比

我們看到上面描述中提到了O()來體現(xiàn)算法時(shí)間復(fù)雜度，也被稱為大O計(jì)法。大O用于表示上界，即用于表示算法最壞情況下運(yùn)行時(shí)間的上界，也就是在最壞情況下運(yùn)行所花費(fèi)的時(shí)間。

推導(dǎo)大O階方法：

• 用常數(shù)1取代運(yùn)行時(shí)間中的所有加法常數(shù)
• 在修改后的運(yùn)行函數(shù)次數(shù)中，只保留最高階項(xiàng)
• 如果最高階項(xiàng)存在且不是1，則去除與這個(gè)項(xiàng)相乘的常數(shù)

接著，我們自己動(dòng)手練習(xí)下算法時(shí)間復(fù)雜度的計(jì)算方法，如下：

function testFunc(n){ 
  for(let i = 0; i < n; i += i){ //執(zhí)行1+log2(n)次 
    for(let j = 0; j < n; j++){ //執(zhí)行n+1次 
      console.log("yichuan");//執(zhí)行(1+log2(n))*(n+1)次 
    } 
  } 
} 

我們看到，在第一次for循環(huán)中，i+=i即i=i+i=2i，那么當(dāng)2i=n時(shí)得到n=log2(n)，要跳出循環(huán)即要執(zhí)行1+log2(n)次語句。而在第二次for循環(huán)中語句要執(zhí)行n+1次才能跳出循環(huán)，而打印語句的執(zhí)行次數(shù)是(1+log2(n))*(n+1)次。其實(shí)采用大O記數(shù)法忽略加法常數(shù)和最高次項(xiàng)系數(shù)，那么得到就是執(zhí)行nlogn次，記作O(nlogn)。

記住，在計(jì)算算法時(shí)間復(fù)雜度時(shí)，可以根據(jù)高階次數(shù)的實(shí)際情況忽略其加法常數(shù)和最高次項(xiàng)系數(shù)、對數(shù)項(xiàng)的底數(shù)。

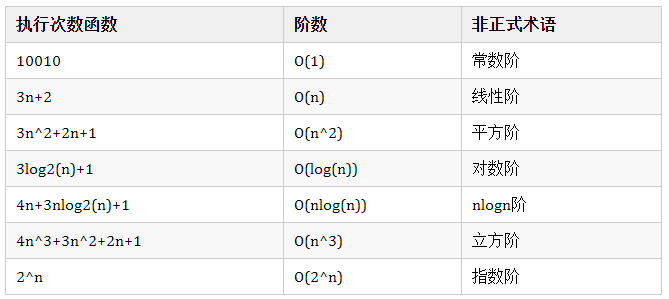
常見的計(jì)數(shù)階數(shù)有：

我們可以看到常見的算法時(shí)間復(fù)雜度計(jì)算階數(shù)所耗費(fèi)時(shí)間的比較：

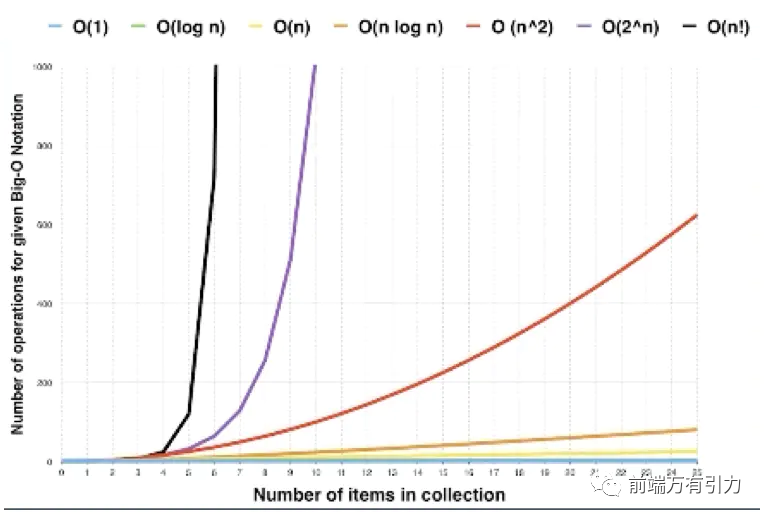
各種時(shí)間復(fù)雜度曲線如下：

算法空間復(fù)雜度

其實(shí)，在代碼時(shí)完全是犧牲空間來換取時(shí)間。類比于算法時(shí)間復(fù)雜度，空間復(fù)雜度表示算法存儲(chǔ)空間與數(shù)據(jù)規(guī)模之間的增長關(guān)系。

算法空間復(fù)雜度：通過計(jì)算算法所需的存儲(chǔ)空間實(shí)現(xiàn)，而計(jì)算公式是：S(n)=O(f(n))。

• n表示問題的規(guī)模
• f(n)表示語句中關(guān)于n所占存儲(chǔ)空間的函數(shù)

function spaceFunc(n){ 
  const arr = [];//第2行代碼 
  arr.length = n;//第3行代碼 
  for(let i = 0; i < n; i++){ 
    arr[i] = i * i; 
  } 
   
  for(let j = n - 1; j >= 0; --j){ 
    console.log(arr[i]); 
  } 
} 

觀察上述代碼可得：在第2行代碼中，在內(nèi)存開辟一塊空間存儲(chǔ)變量arr并對其賦值空數(shù)組;在第3行代碼中，將數(shù)組的長度設(shè)置為n，數(shù)組中會(huì)自動(dòng)填充n個(gè)undefined;此外剩下代碼并未占據(jù)更多空間，因此整段代碼的空間復(fù)雜度為O(n)。

最壞情況和平均情況

最壞情況運(yùn)行時(shí)間是這段程序在運(yùn)行所耗費(fèi)時(shí)間最多的情況，沒有比這更糟糕的情況。通常，我們提到的運(yùn)行時(shí)間指的都是最壞情況的運(yùn)行時(shí)間。

平均情況運(yùn)行時(shí)間所指的是程序所期望的平均時(shí)間，但是在實(shí)際測試中，很難通過分析得到，需要通過一定數(shù)量的實(shí)驗(yàn)數(shù)據(jù)和估算。

我們知道，在進(jìn)行查找n個(gè)隨機(jī)數(shù)中查找某個(gè)數(shù)字，最好的情況是查找第1個(gè)數(shù)字就找到，此時(shí)的時(shí)間復(fù)雜度是O(1)，而最壞的情況下是查找到第n個(gè)數(shù)字才找到。那么，在查找數(shù)字的算法中最壞情況的時(shí)間復(fù)雜度是O(n)，平均情況的時(shí)間復(fù)雜度是O((1+n)/2)即O(n/2)。

小結(jié)

在本文中，筆者介紹了什么是算法、為什么要用算法、如何衡量算法的時(shí)間復(fù)雜度和空間復(fù)雜度以及算法的最壞情況和平均情況的概念。