?譯者 | 朱先忠
審校 | 孫淑娟
1.簡介
貝葉斯定理為我們提供了一種根據新證據更新信念的方法——當然,還要考慮到我們先前信念的強度。運用貝葉斯定理,你可以試圖回答這樣一個問題:根據新的證據,我的假設的可能性是多少?
在本文中,我們將討論貝葉斯定理可以改善數據科學實踐的三種方法:
- 更新
- 溝通
- 分類
到文章最后,我相信您將對貝葉斯定理有關的基本概念有一個深刻的理解。
2.方法1:更新
貝葉斯定理為檢驗假設提供了一種結構,同時考慮了先驗假設和新證據的強度,這個過程稱為貝葉斯更新。
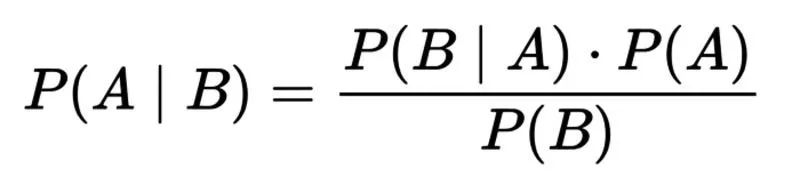
貝葉斯定理:其中A代表假設,B代表與假設相關的新證據
換句話說,這個公式是“在給定B的情況下,A發生的概率等于給定A的情況下B發生的概率乘以A發生的概率除以B發生的概率。”
讓我們再深入分析一下這個公式(注意其中含有隨機變量的定義內容):
“根據新證據作出假設的概率等于新證據成立的概率(假定假設成立)乘以觀察到新證據之前假設成立的概率,除以新證據成立的概率。”
這種表述可以進一步縮短為:
“后驗概率等于似然(likelihood)乘以先驗概率除以邊際似然(marginal likelihood)。”
不管貝葉斯定理現在聽起來是否直觀,我保證你會一直使用它的。
真實世界示例
比方說,你的朋友打電話來告訴你,她很抱歉,她今晚不能來吃飯。她最近收養了一只寵物考拉,它患上了感冒流鼻涕。她真的需要呆在家里監視考拉的癥狀情況。
你的假設是,你的朋友不會無緣無故地拋棄你。那么,考慮到她新寵物的最新癥狀,你的假設成立的似然(likelihood)有多大?

為了評估我們的朋友因為照顧考拉而不在家吃飯的后驗概率,我們需要考慮你的朋友需要和考拉呆在家里的概率,因為假設你的朋友是一個正直的人,不會無故放棄晚餐計劃。你可能會得出這樣的結論:一個通常負責的好朋友很可能會呆在家里照顧寵物。
接下來,我們將似然(likelihood)乘以先驗概率。在你的朋友打電話之前,你對她的晚餐計劃有多大的信心?如果你認為你的朋友堅如磐石,通常不愿意在最后一刻改變計劃,那么你的先驗概率很大,無論有什么新的證據,你都不太可能改變這種觀點。另一方面,如果你的朋友很脆弱,而你已經想知道她是否會打電話取消,那么你的先驗概率很小,這也可能會讓她關于和考拉待在家里的說法受到質疑。
最后,我們將上述計算結果除以你的朋友和考拉呆在家里的邊際似然。
貝葉斯推理是建立在這種靈活的、常識性的方法基礎上的,這種方法根據我們先驗知識的強度和新證據的概率來更新我們關于世界的模型。事實上,貝葉斯定理的最初應用是評估上帝的存在。
當涉及到生命和數據科學的關鍵問題時,你不能抨擊貝葉斯定理是一種直觀的評估信念如何隨時間變化的方法。
3.方法2:溝通
正如貝葉斯定理可以幫助你理解和闡明面對新證據如何更新理論一樣,貝葉斯也可以讓你成為更強大的數據科學傳播者。
數據科學從根本上講是關于應用數據改進決策的一門科學。
“只有兩件事決定你的生活結果:運氣和你的決策質量。你只能控制這兩件事中的一件。”
——安妮·杜克,撲克游戲冠軍兼作家
提高決策質量通常意味著說服決策者。正如每個人的情況一樣,您的組織中的決策者正在參與對話。
真實世界示例
我曾經是一家熱氣球制造商的顧問。我的任務是幫助建立一個數據庫,以提高客戶對其供應鏈、制造流程和銷售的端到端的理解。
第一天,工廠經理帶我們參觀了工廠,他自豪地描述了一份新的供應商合同,該合同涉及更輕質、更便宜的原材料。
但有一個問題。當我的團隊聯系來自整個企業不同數據源的數據表時,我們發現來自新供應商的材料與廢料增加2.5%之間存在一定聯系。

工廠經理有一個非常強烈的預感,那就是新供應商對他的業務來說很受益。但是,我們卻提供了一些相反的證據——我們使用了貝葉斯定理,因為我們理解這樣一個事實,即:先驗知識越強,需要改變它的證據就越多。
在向工廠經理提出我們的調查結果之前,我們需要收集一些額外的證據來證明不存在導致不同廢料水平的其他因素(如磨損的機器、新員工、環境條件等)。
最后,我們向經理提供了更多證據,并幫助他重新談判供應商合同。
4.方法3:分類
貝葉斯定理可以應用于文本分析的場景,這是一種稱為樸素貝葉斯的技術,因為它樸素地假設數據集中每個輸入變量(在本例中為每個單詞)是獨立的。
真實世界示例
假設你發現了一堆你祖父母寫的信。他們之間有著一段“動蕩不安”的關系,并且有足夠的戲劇性浪漫故事——并不局限于真人秀節目中的年輕人間發生的那種。

您需要構建一個情感分類器來確定大部分內容是正面的還是負面的。這其中的一種方法是利用樸素貝葉斯定理。
像樸素貝葉斯這樣的生成式分類器將構建一個類別(在本例中為正面的或者是負面的)模型;然后,根據此類別生成一些輸入數據。給出一個觀察結果(來自字母測試語料庫的一個新句子),它返回最有可能產生觀察結果的類別。這與學習輸入特征預測能力的判別式模型分類器(如邏輯回歸)形成對比。
樸素貝葉斯(Naive Bayes)是建立在單詞袋技術基礎上的。其基本思想是,將文檔轉換為直方圖,以便統計每個單詞的使用次數。
您可以使用我們在第#1部分中研究過的稍微修改過的貝葉斯推斷公式來計算每個觀測值的最可能類別。其實,上面簡單修改的是樸素貝葉斯的樸素部分:即假設每個單詞的概率在給定的類別中是獨立的,于是我們可以將它們相乘,以生成句子隨類別一起“落下”的概率。
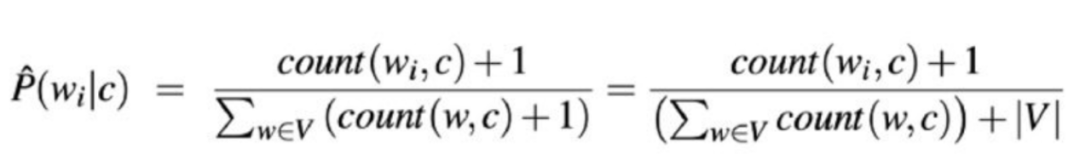
語音和語言處理公式(作者:Daniel Jurafsky和James H.Martin)
在上述公式中,wi表示文檔c中單詞的計數。公式的分母是單詞屬于給定類別的條件概率之和。
公式中的+1防止了在類別中沒有觀察到單詞的情況下乘以零的可能性。這種添加一個的技術稱為拉普拉斯平滑。
最后,|V|由所有類別中所有單詞的并集組成。
貝葉斯定理相關詞匯
- 后驗概率:根據新證據提出假設的可能性。
- 似然(likelihood):假定假設為真,證據為真的可能性。
- 先驗概率:在新證據出現之前,相信假設是真實的。
- 邊際似然:證據。
- 樸素貝葉斯:一種分類器算法,它假設數據集的特征之間具有樸素的獨立性。
- 生成式分類器:建模特定類,以便確定如何生成輸入數據;即是已知類別確定樣本。
- 單詞袋:將文檔轉換為直方圖的簡化文本表示。
- 拉普拉斯平滑:一種簡單的加法平滑技術,可避免乘以零。
5.小結
我有一個強烈的先驗信念,即貝葉斯定理對數據科學家十分有用;但是,我還是會根據您在評論中給我的反饋來更新后驗概率。總之,我期待著您的來信,告訴我您是如何在生活和工作中使用貝葉斯定理的。
原文鏈接:https://www.kdnuggets.com/2022/06/3-ways-understanding-bayes-theorem-improve-data-science.html
譯者介紹
朱先忠,51CTO社區編輯,51CTO專家博客、講師,濰坊一所高校計算機教師,自由編程界老兵一枚。早期專注各種微軟技術(編著成ASP.NET AJX、Cocos 2d-X相關三本技術圖書),近十多年投身于開源世界(熟悉流行全棧Web開發技術),了解基于OneNet/AliOS+Arduino/ESP32/樹莓派等物聯網開發技術與Scala+Hadoop+Spark+Flink等大數據開發技術。?





























