使用可視化工具和統計方法檢測異常值
異常值(離群值)是指距離其他數據值太遠的數據值。數據異常值可能是自然產生的,也可能是由于測量不準確、或系統故障造成的。與缺失值類似,異常值會破壞數據科學項目并返回錯誤的結果或預測。異常值也可能出現在傾斜數據中,這些類型的異常值被認為是自然異常值。
異常值會影響數據的平均值、標準差和四分位范圍。如果我們在去除異常值之前和之后計算這些統計數據,我們會得到不同的結果。
Carla Martins
異常值如何影響機器學習模型?
如果我們的異常值是自然的而不是由于測量誤差,則應該將它保留在數據集中,并執行數據轉換來對其進行規范化處理。如果我們的數據集很大,但異常值很少,我們應該保留這些異常值,因為它們不會顯著影響結果,并且可以為我們的模型帶來泛化的效果。
如果我們非常確定我異常值是由于測量誤差帶來的,則應該從數據集中刪除它們。去除異常值的將減少數據集的大小,并可以讓我們的模型的適用到所包含的度量范圍。但是要記住去掉自然異常值可能導致模型不準確。
使用可視化工具檢測異常值
異常值是不容易被“肉眼”發現的,但是有一些可視化工具可以幫助完成這項任務。最常見的是箱形圖和直方圖。
和往常一樣,我們第一步是加載必要的庫和導入/加載數據集。這里將使用??insurance.csv??。
import numpy as np
import pandas as pd
import seaborn as sns
import statistics
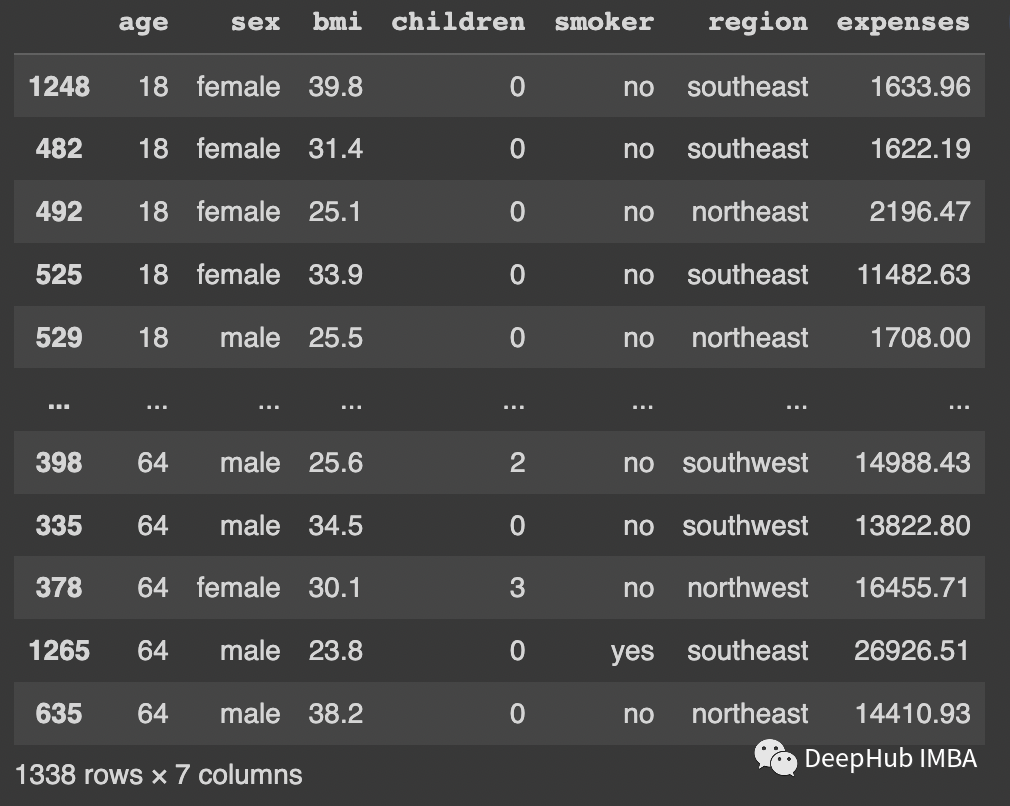
df = pd.read_csv('insurance.csv')
df
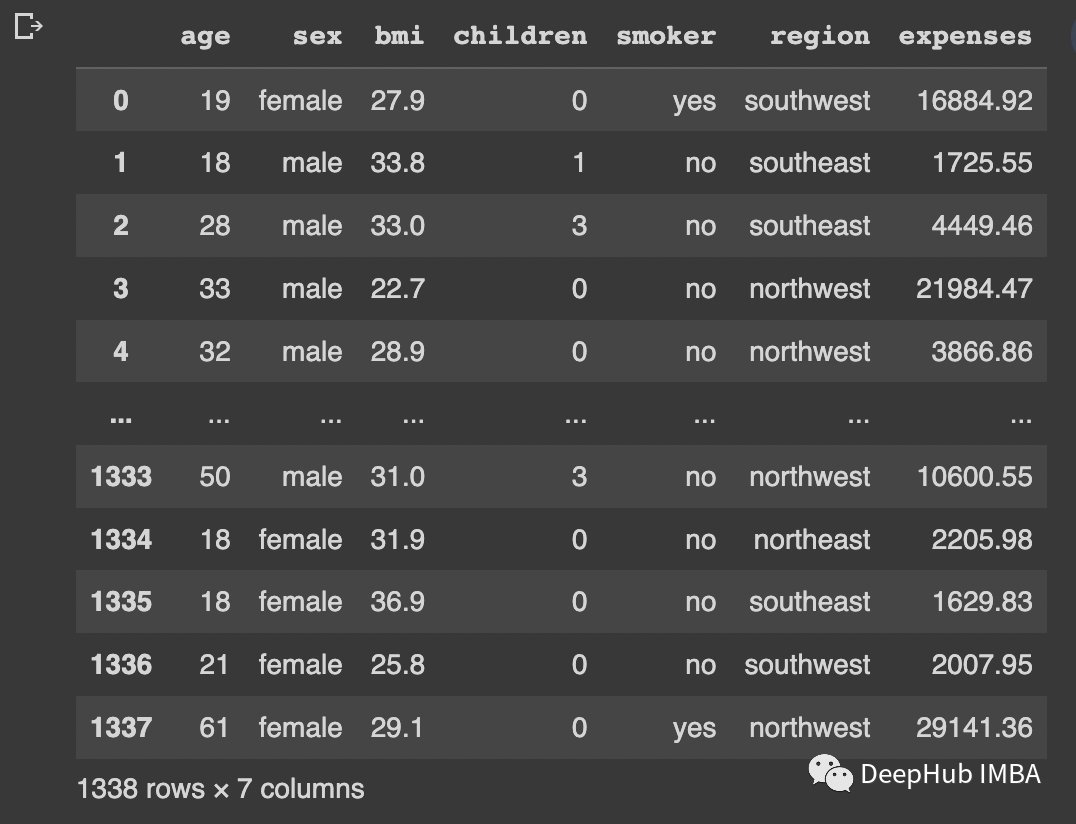
我們將檢查age,bmi和expenses的異常值。
第一種方法是用box - plot表示數據分布:
sns.boxplot(y="age", data=df)
sns.boxplot(y="bmi", data=df)
sns.boxplot(y="expenses", data=df)
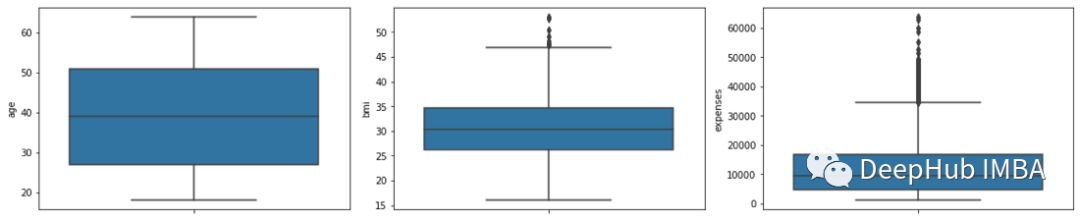
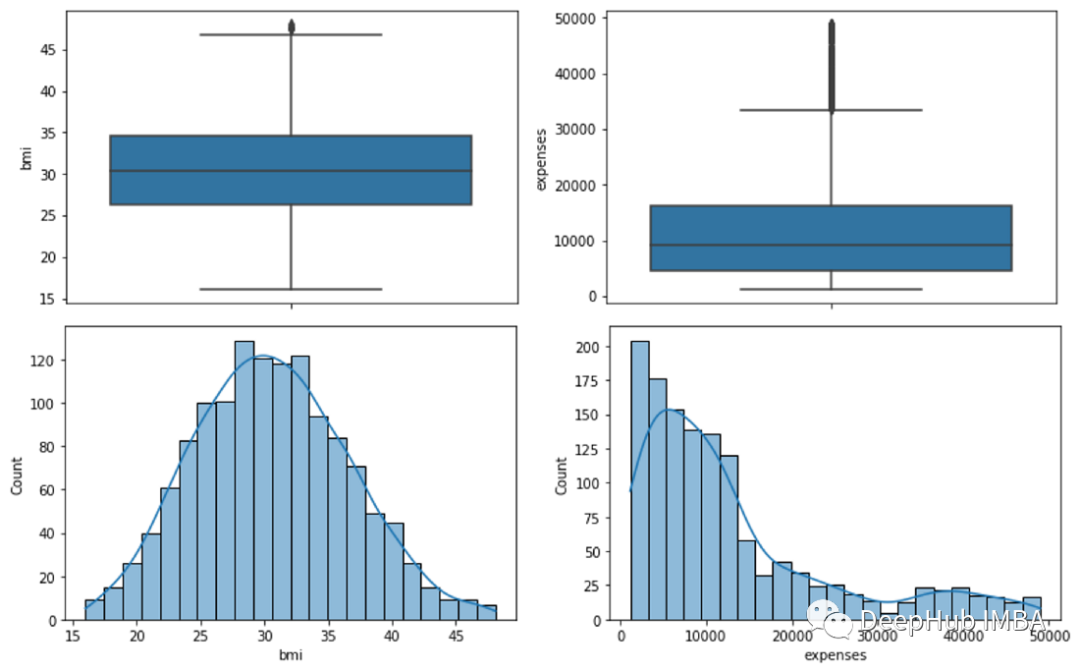
從箱線圖我們可以看到age沒有異常值bmi在上界有一些異常值,而expenses在上界有很多異常值,這表明了這是一個偏態分布。為了檢查這個偏態分布的傾斜程度,我們將使用直方圖。
sns.histplot(df, x="age", kde=True)
sns.histplot(df, x="bmi", kde=True)
sns.histplot(df, x="expenses", kde=True)
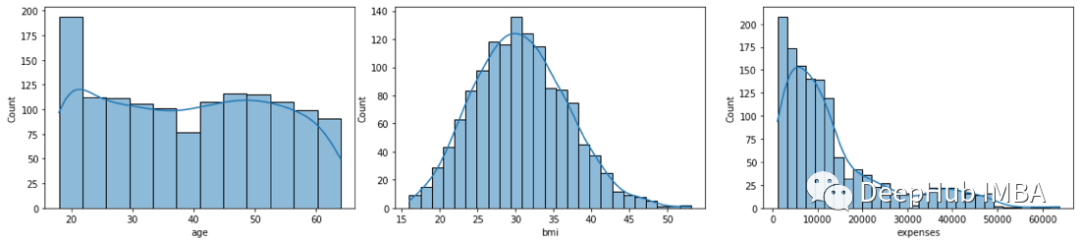
從直方圖中可以看出,年齡變量均勻分布,bmi接近正態分布,expenses偏態分布。通過分析這兩種圖形表示,我們可以決定要排除那些數據。對于年齡不排除任何值。對于bmi我們將排除高于47的值,對于費用,我們將排除高于50000的值。
df.drop(df[df['bmi'] >= 47].index, inplace = True)
df.drop(df[df['expenses'] >= 50000].index, inplace = True)
現在如果再次檢查箱線圖和直方圖:
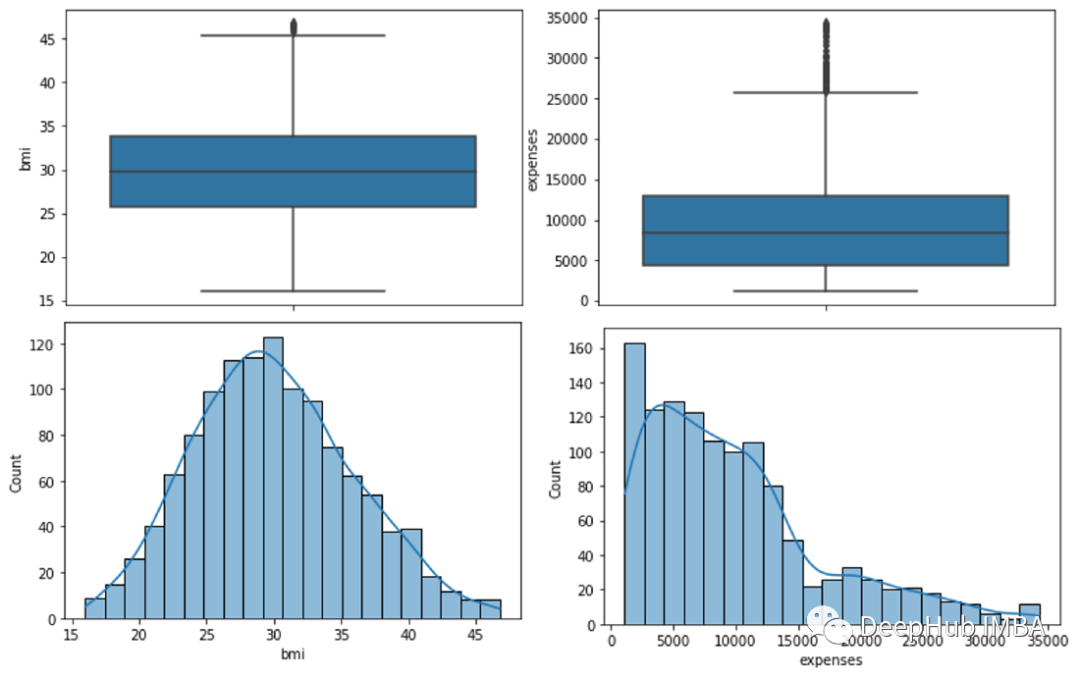
用統計方法檢測異常值
有兩種主要的統計方法可以檢測異常值:使用z分數和使用四分位范圍。
1、使用Z-score檢測異常值
Z-score是一種數學變換,根據其與均值的距離對每個觀察結果進行分類。與平均值之間的距離用標準差(SD)來衡量。如果得到的數值為1.59,我們就知道觀察值比平均值高出1.59個標準差。同理如果得到-2.4的Z-score,我們就會知道觀察值比平均值低-2.4個標準差。高于3SD或低于-3SD的觀測值一般會被認為是異常值。
下面我們用代碼實現,首先查看age:
df = pd.read_csv('insurance.csv')
mean_age = statistics.mean(df['age'])
stdev_age = statistics.stdev(df['age'])
age_z_score = (df['age']-mean_age)/stdev_age
df['age_z_score'] = age_z_score.tolist()
現在查看是否有低于-3SD的值:
df.sort_values(by=['age_z_score'], ascending=True)
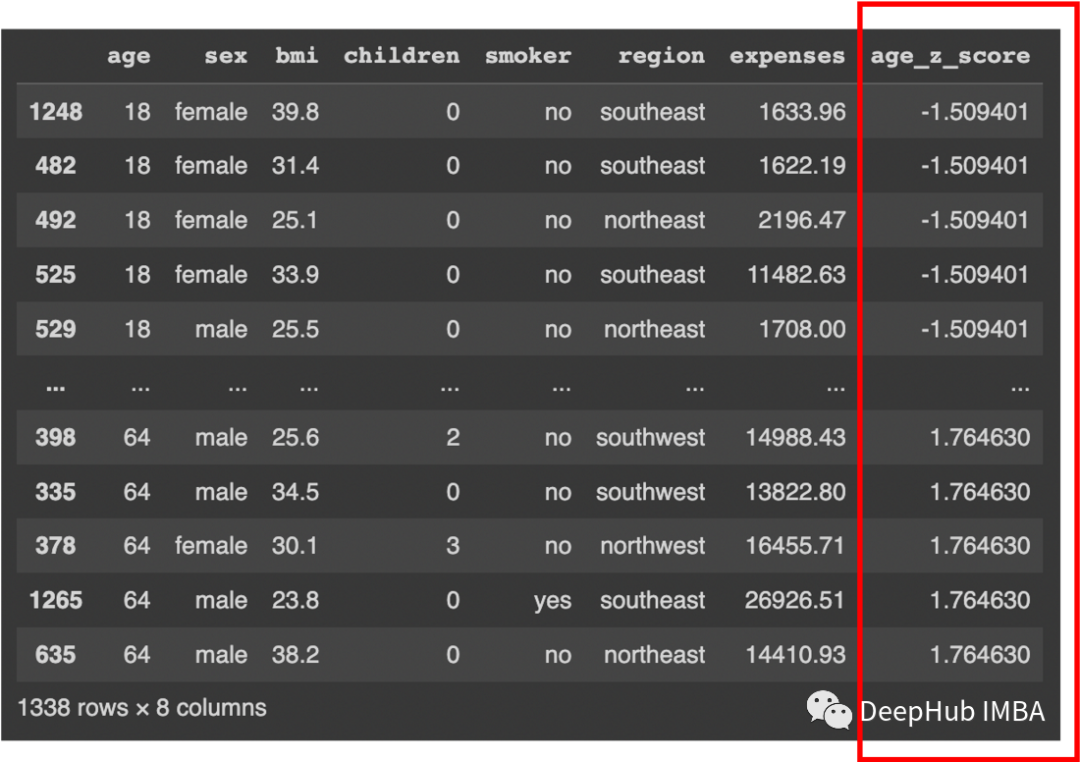
可以看到沒有低于-3SD的值。現在檢查3SD以上的值:
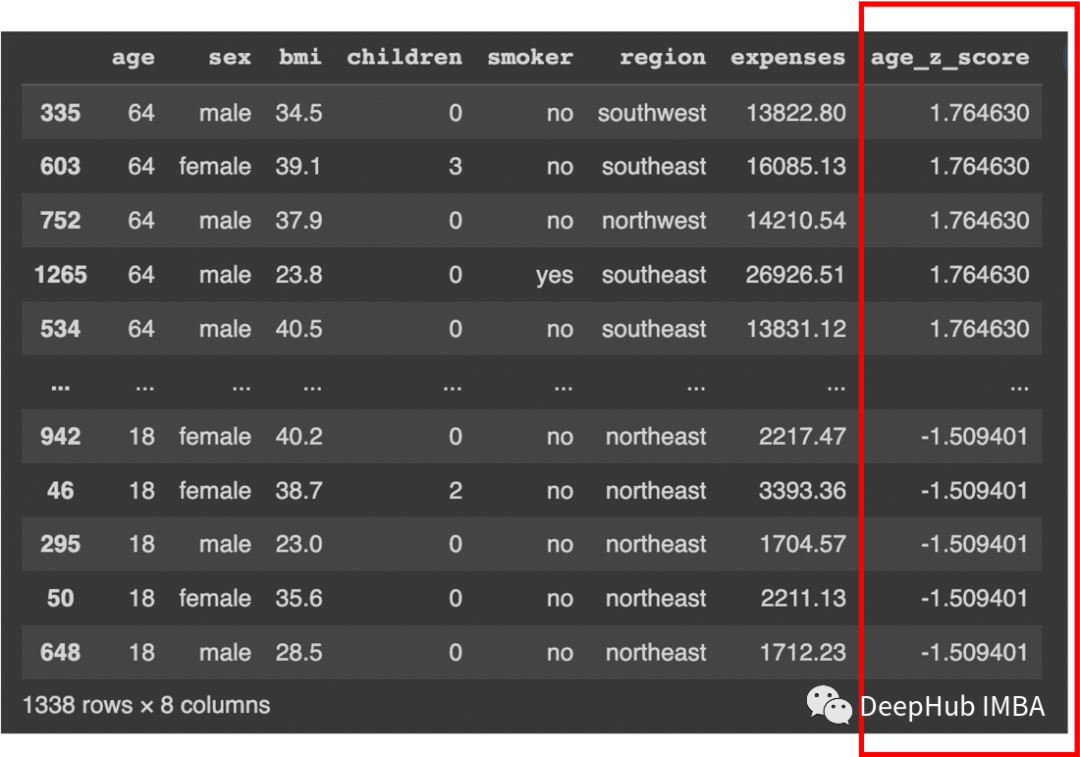
我們可以看到沒有高于3SD的值。也就是說age沒有異常值。現在對變量bmi做同樣的操作:
mean_bmi = statistics.mean(df['bmi'])
stdev_bmi = statistics.stdev(df['bmi'])
bmi_z_score = (df['bmi']-mean_bmi)/stdev_bmi
df['bmi_z_score'] = bmi_z_score.tolist()
df.sort_values(by=['bmi_z_score'], ascending=True)
df.sort_values(by=['bmi_z_score'], ascending=False)
查看3SD以上的值:
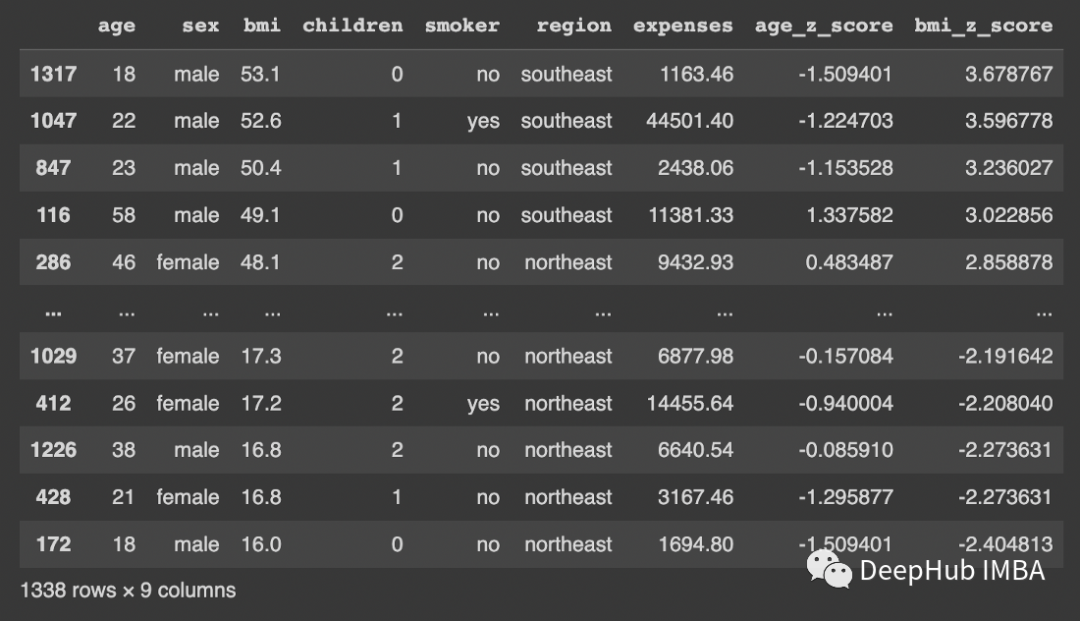
將這些值刪除:
df.drop(df[df[‘bmi_z_score’] >= 3].index, inplace = True)
下一步用同樣的方法計算expenses:
mean_expenses = statistics.mean(df['expenses'])
stdev_expenses = statistics.stdev(df['expenses'])
expenses_z_score = (df['expenses']-mean_expenses)/stdev_expenses
df['expenses_z_score'] = expenses_z_score.tolist()
df.sort_values(by=['expenses_z_score'], ascending=True)
df.sort_values(by=['expenses_z_score'], ascending=False)
df.drop(df[df[‘expenses_z_score’] >= 3].index, inplace = True)
刪除了數據以后,我們再次可視化數據:
可以看到,一些值已經被移除了
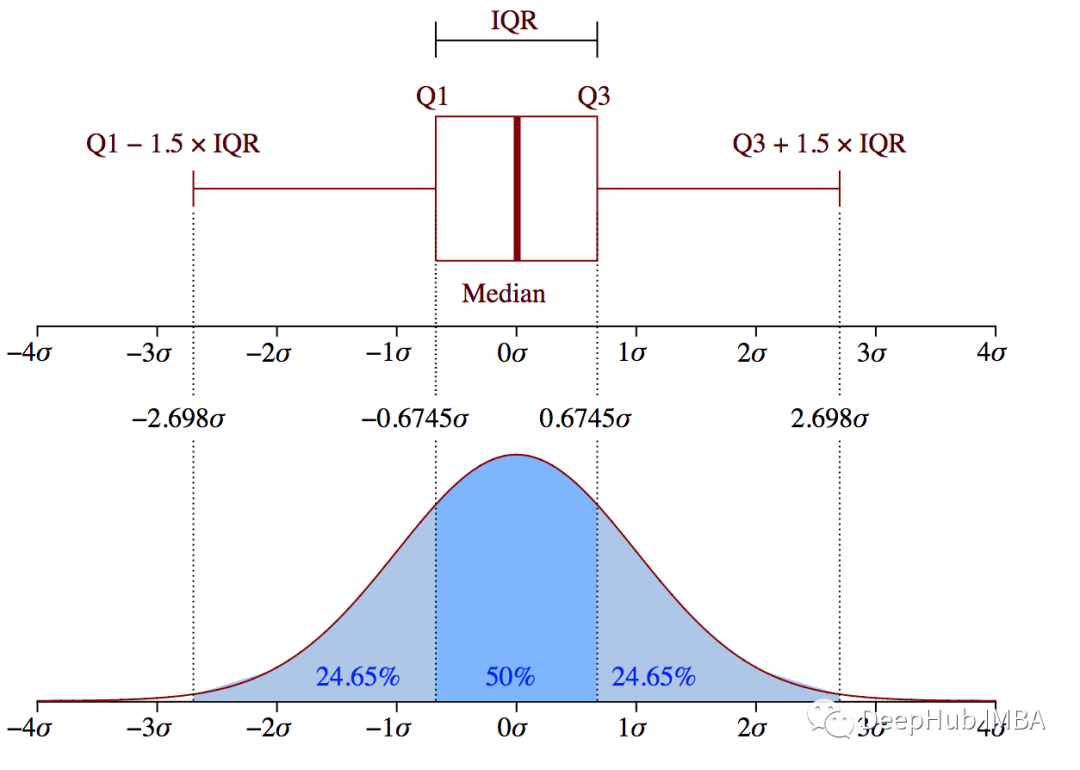
2、使用四分位距檢測異常值
四分位距將數據分布到四個部分,并且從低到高排序,如下圖所示,每個部分包含相同數量的樣本。第一個四分位(Q1)是邊界上的數據點的值。Q2和Q3也是如此。四分位距(IQR)是兩個中間部分的數據點(代表50%的數據)。四分位距包含所有高于Q1低于Q3的數據點。如果該點高于Q3 + (1.5 x IQR),則表示包含較高數值離群值,如果Q1?(1.5 x IQR)則存在較低數值的離群值。
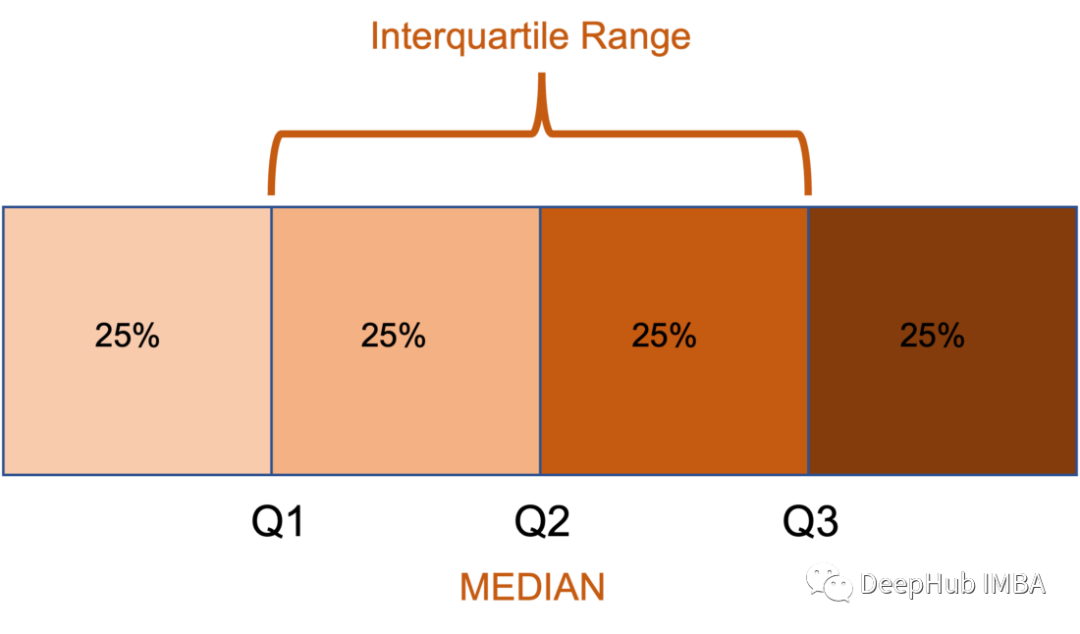
代碼如下:
df = pd.read_csv('insurance.csv')
q75_age, q25_age = np.percentile(df['age'], [75 ,25])
iqr_age = q75_age - q25_age
iqr_age
age_h_bound = q75_age+(1.5*iqr_age)
age_l_bound = q25_age-(1.5*iqr_age)
print(age_h_bound)
print(age_l_bound)
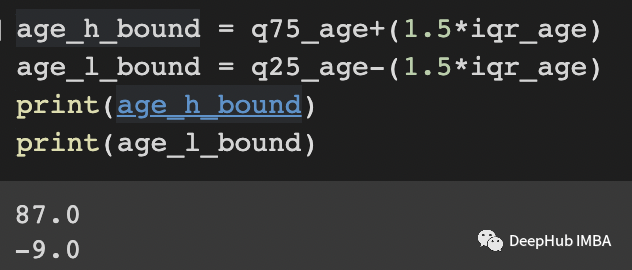
這樣就知道了異常值位于87以上或-9以下:
df.sort_values(by=['age'], ascending=True)
可以看到沒有下異常值,現在我們將檢查上異常值:
df.sort_values(by=['age'], ascending=False)
也沒有上異常值。
下面對bmi執行同樣的操作:
q75_bmi, q25_bmi = np.percentile(df['bmi'], [75 ,25])
iqr_bmi = q75_bmi - q25_bmi
iqr_bmi
bmi_h_bound = q75_bmi+(1.5*iqr_bmi)
bmi_l_bound = q25_bmi-(1.5*iqr_bmi)
print(bmi_h_bound)
print(bmi_l_bound)
df.sort_values(by=['bmi'], ascending=True)
df.sort_values(by=['bmi'], ascending=False)
df.drop(df[df['bmi'] >= 47.3].index, inplace = True)
df.drop(df[df['bmi'] <= 13.7].index, inplace = True)
expenses也是用相同的方法進行處理,我們對結果進行可視化:
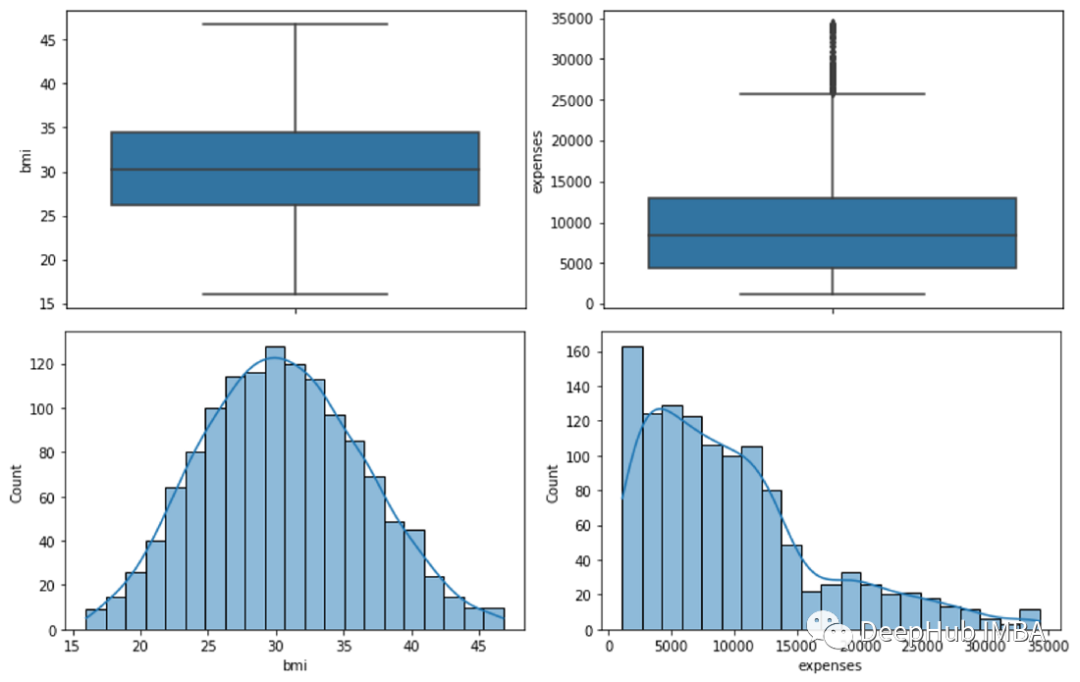
可以看到異常值也被刪除了。