二叉樹的后序遍歷序列

作者：神奇的程序員 2022-10-26 23:58:02

開發前端

有一個整數數組，如何判斷該數組是不是某個二叉樹的后序遍歷結果？本文就跟大家分享下這個算法。

前言

有一個整數數組，如何判斷該數組是不是某個二叉樹的后序遍歷結果？本文就跟大家分享下這個算法，歡迎各位感興趣的開發者閱讀本文。

思路分析

我們通過一個例子來分析這個問題，如下所示為一顆二叉樹。

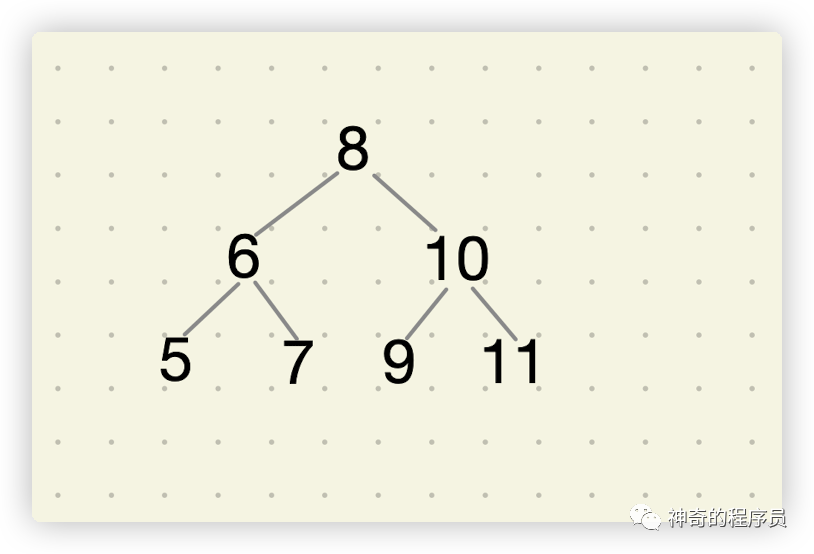
通過之前文章的學習（二叉樹的后序遍歷），我們可以很快看出這顆樹的后序遍歷序列為: [5, 7, 6, 9, 11, 10, 8]，通過觀察后我們發現最后一個數字為二叉樹的根節點，數組中前面的數字可以分為兩部分：

第一部分是左子樹節點的值，它們都比根節點的值小

第二部分是右子樹節點的值，它們都比根節點的值大

在上面的后序遍歷結果數組中，前3個數字5、7、6?都比根節點8小，是它的左子樹節點；后3個數字9、11、10都比根節點8大，是它的右子樹節點。

那么，我們就可以用同樣的方法來確定數組每一部分對應的子樹的結構。

數組5, 7, 6，最后一個數字6是左子樹的根節點的值。數字5比6小，是6的左子節點，7則是它的右子節點

數組9, 11, 10，最后一個數字10是左子樹的根節點的值。數字9比10小，是10的左子節點，11則是它的右子節點

實現思路

通過上面的分析，我們便可以總結出實現思路了。

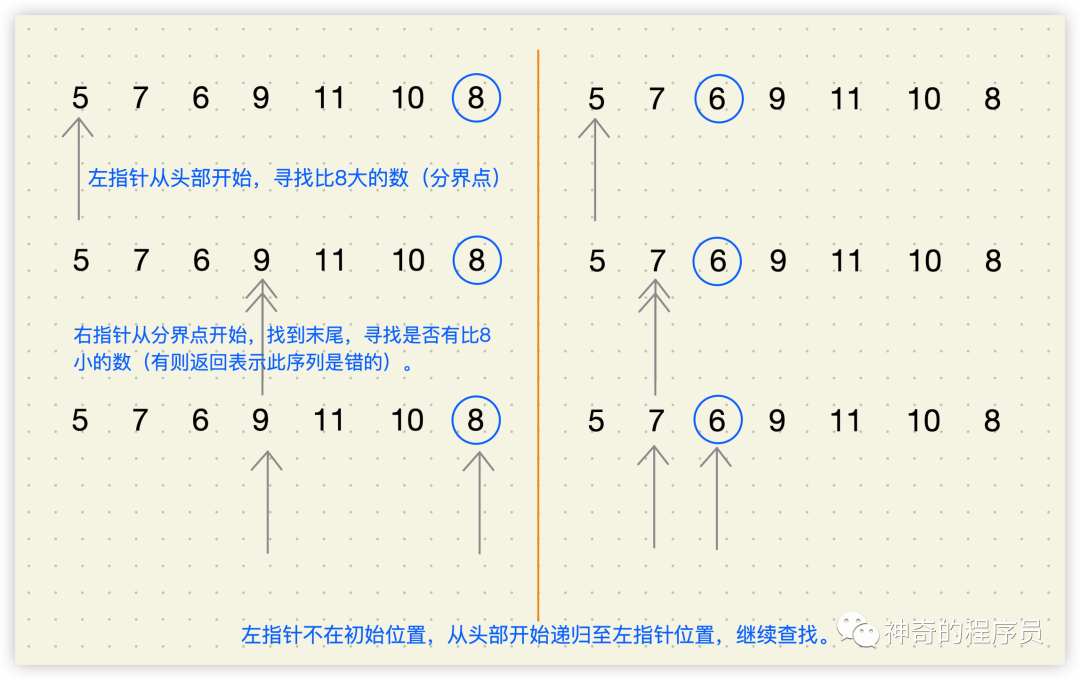
最后一項一定是根節點，從根節點前面的值中尋找左、右子樹的分界點

定義指針leftIndex，前半部分一定是它的左子樹，每個節點的值都比根節點小

leftIndex默認從0開始，逐漸遞增，尋找比根節點大的值，便是它們的分界點

定義指針rightIndex，后半部分一定是它的右子樹，每個節點的值都比根節點大。

rightIndex從分界點開始找（默認從leftIndex位置開始），如果有比根節點小的值，那么這個序列一定不屬于二叉樹的后序遍歷序列

如果leftIndex指針離開了起始位置（0），證明它的左子節點還沒找完，需要重復執行上述過程繼續查找（遞歸尋找到數組的leftIndex位置）

如果leftIndex指針沒有到達數組末尾，證明它的右子節點還沒找完，需要重復執行上述過程繼續查找（從leftIndex+1位置開始遞歸）

返回左、右子樹的遞歸校驗結果（兩者都為true則表示這個序列為二叉樹的后序遍歷序列）

實現代碼

捋清楚思路后，我們便可以順利的寫出代碼了。

  verifySequenceOfBST(sequence: Array<number>, length: number): boolean {
    if (sequence == null || length <= 0) return false;
    const root = sequence[length - 1];
    // 左子樹節點的值小于根節點的值
    let leftIndex = 0;
    for (; leftIndex < length - 1; leftIndex++) {
      if (sequence[leftIndex] > root) {
        break;
      }
    }
    // 右子樹節點的值大于根節點的值
    let rightIndex = leftIndex;
    for (; rightIndex < length - 1; rightIndex++) {
      if (sequence[rightIndex] < root) {
        return false;
      }
    }

    // 判斷左子樹是否為二叉樹
    let leftVerify = true;
    if (leftIndex > 0) {
      leftVerify = this.verifySequenceOfBST(sequence, leftIndex);
    }
    let rightVerify = true;
    if (leftIndex < length - 1) {
      rightVerify = this.verifySequenceOfBST(
        sequence.slice(leftIndex + 1),
        length - leftIndex - 1
      );
    }
    return leftVerify && rightVerify;
  }

測試用例

接下來我們將思路分析中所列舉的例子代入上述代碼，來驗證下我們的代碼能否正確執行。

const arr = [5, 7, 6, 9, 11, 10, 8];
console.log("比對結果", treeOperateTest.verifySequenceOfBST(arr, arr.length));

我們再列舉一個錯誤的例子，來驗證下它能否正確判斷。

const arr = [7, 4, 6, 5];
console.log("比對結果", treeOperateTest.verifySequenceOfBST(arr, arr.length));

示例代碼

本文用到的代碼完整版請移步：

TreeOperate.ts
TreeOperate-test.ts

責任編輯：武曉燕來源：神奇的程序員

二叉樹數組算法

成人免费xxxxx在线视频软件_久久精品久久久_亚洲国产精品久久久_天天色天天色_亚洲人成一区_欧美一级欧美三级在线观看